深度强化学习 — 确定性策略梯度类算法
DDPG
算法思想
1. 从 PG 到 DPG,再到 DDPG
-
PG(Policy Gradient) :随机策略(stochastic policy)通过一个概率分布函数 𝜋𝜃πθ, 来表示每一步的最优策略, 在每一步根据该概率分布进行action采样,获得当前的最佳action取值
𝑎𝑡∼𝜋𝜃(𝑠𝑡|𝜃𝜋)
-
PG 的缺陷:
在高维的action空间的频繁采样,无疑是很耗费计算能力的
-
DPG( Deterministic Policy Gradient): 即确定性的行为策略,每一步的行为通过函数μ直接获得确定的值 :𝑎𝑡=𝜇(𝑠𝑡|𝜃𝜇)
DDPG是将深度学习神经网络融合进DPG的策略学习方法
2. DDPG 也可以看作是 DQN 在连续动作空间的延申
DQN是一种基于值函数的方法,基于值函数的方法难以应对的是大的动作空间,特别是连续动作情况
传统的 DQN 网络输出各节点对应各离散动作的取值,如果改为对应各动作维度,可以表示连续动作空间(既 DDPG中 critic 网络的输出,)但要在每个维度上用贪婪算法进行最大值搜索是很难实现的,就是要计算每个 state 下对应的所有动作的 Q 值,然后从中找最值。
DQN cannot be straightforwardly applied to continuous domains since it relies on a finding the action that maximizes the action-value function, which in the continuous valued case requires an iterative optimization process at every step.
DDPG 相比于 value based 方法的优势:
- 而 DDPG 是基于 Actor-Critic方法,在动作输出方面采用一个网络来拟合策略函数,直接输出动作,可以应对连续动作的输出及大的动作空间。
- DDPG 中的 critic 也会输出 Q(s,a)值,但只是 Repaly Buffer 中的部分采样经验对应的值,且无需进行最大值搜索,Q(s,a)只用来训练 actor 策略网络,最终的动作由策略网络直接输出
- 还有就是 Actor-Critic 类方法本身的优势,可以结合 value based 和 policy based 方法的特点,既能直接给出最佳策略,又能通过 crtic 对候选的 (s,a) 对进行评估,不断修正 actor 的策略
网络架构
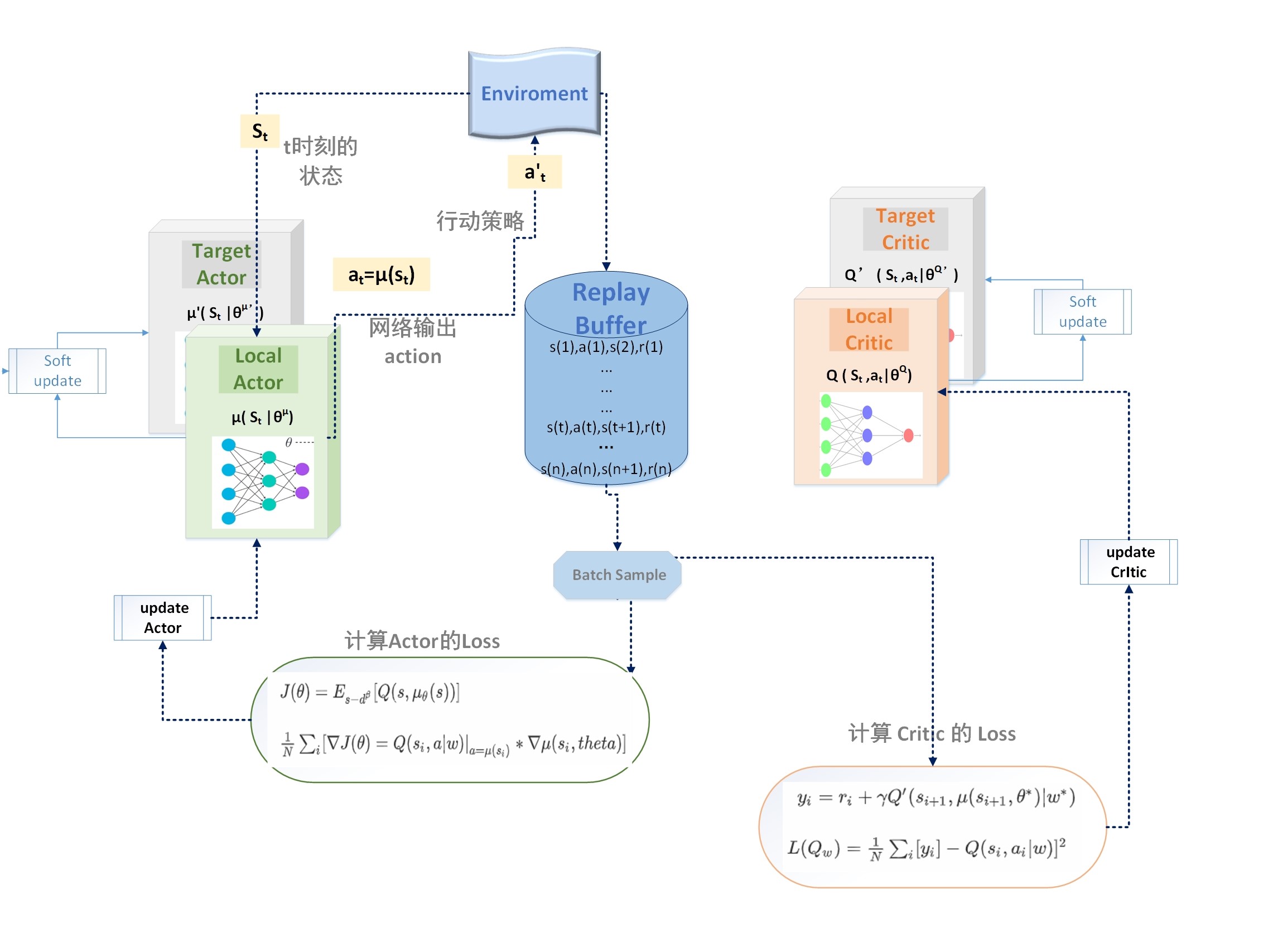
损失函数
1. Actor 网络的 loss function
\(J(\theta)= E_{s-d^\beta} [Q(s,\mu_\theta(s))]\)
\(\frac{1}{N}\sum_i[\nabla J(\theta) = Q(s_i,a|w)|_{a=\mu(s_i)} * \nabla \mu(s_i,theta)]\)
2. Crtic 网络的 loss function
\(y_i = r_i + \gamma Q'(s_{i+1},\mu(s_{i+1},\theta^*)|w^*)\)
$ L(Q_w) = \frac{1}{N} \sum_i [y_i]-Q(s_i,a_i|w)]^2$
算法流程
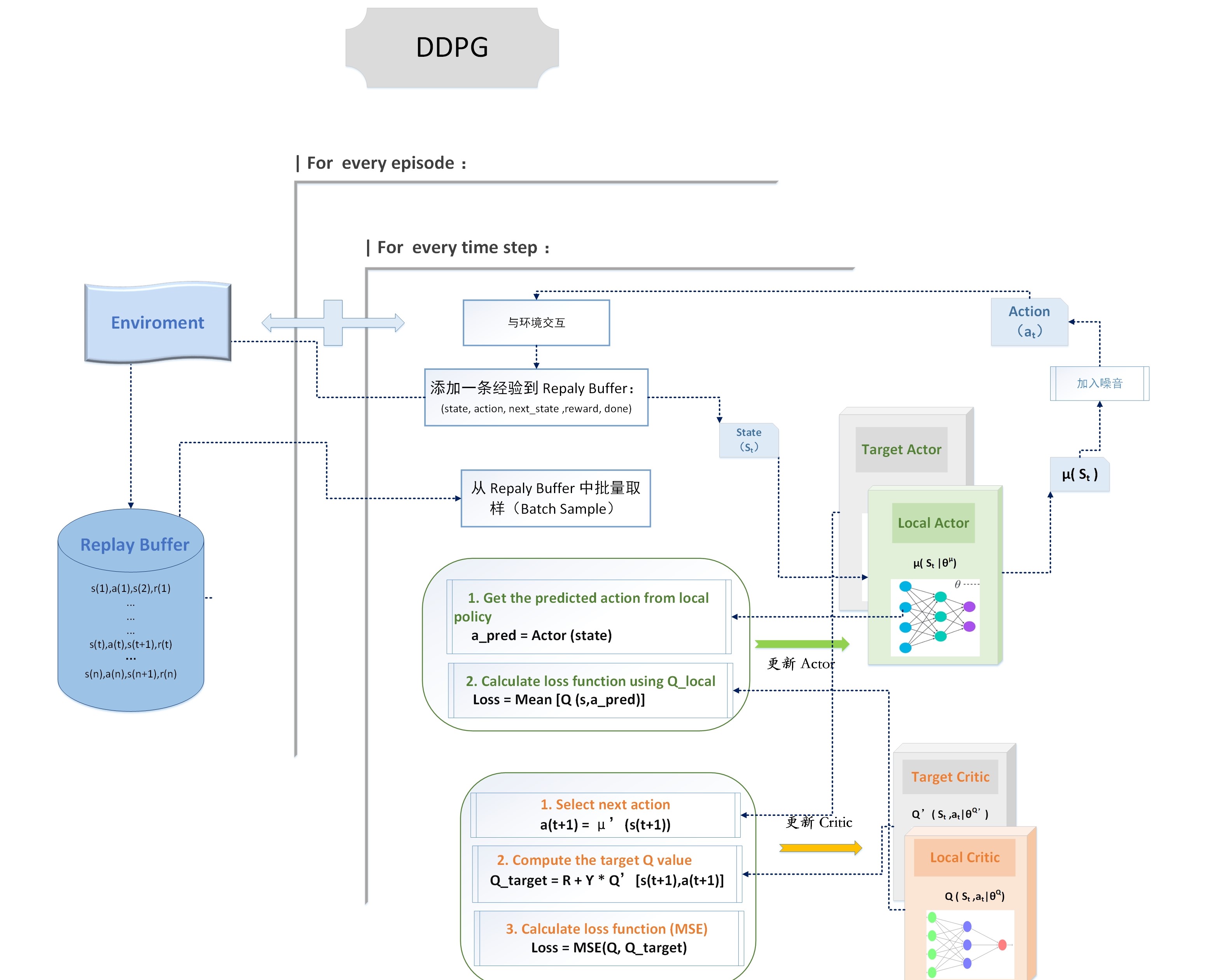
关键设计
1. off policy 随机动作探索
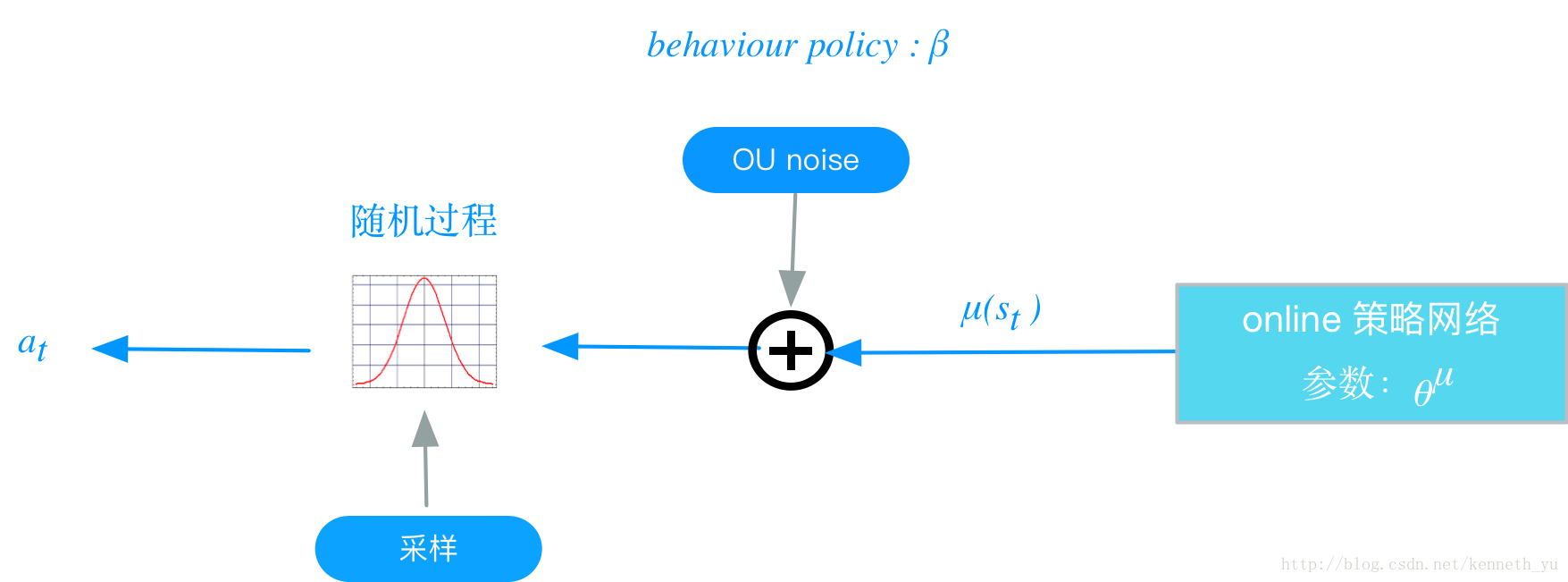
上述这个策略叫做behavior策略,用β来表示, 这时RL的训练方式为离线策略 off-policy
这里与 ϵ−greedy 的思路是类似的。
-
DDPG中,使用Uhlenbeck-Ornstein随机过程(下面简称UO过程),作为引入的随机噪声: UO过程在时序上具备很好的相关性,可以使agent很好的探索具备动量属性的环境
-
这个β不是我们想要得到的最优策略,仅仅在训练过程中,生成下达给环境的action, 从而获得我们想要的数据集,比如状态转换(transitions)、或者agent的行走路径等,然后利用这个数据集去 训练策略μ,以获得最优策略。
-
在test 和 evaluation时,使用μ,不会再使用β
2. Soft update (Copy network)
soft update是一种running average的算法 :
\(\theta ^{Q'} = \tau \theta ^{Q}+ (1-\tau) \theta ^{Q'}\)
\(\theta ^{\mu'} = \tau \theta ^{\mu}+ (1-\tau) \theta ^{\mu'}\)
-
优点:target网络参数变化小,用于在训练过程中计算online网络的gradient,比较稳定,训练易于收敛。
-
代价:参数变化小,学习过程变慢。还有一个问题是使用这种缓慢更新的 target 网络,容易引起对 Q 值的过高估计(over estimation),从而使策略很难收敛,这个缺陷在后续的升级版算法 TD3 中得到了解决。
3. Repaly Buffer
这里沿用了 DQN 中的经验回放策略,打破经验之间的耦合,每次随机批量采样去训练网络参数。
TD3:Twin Delayed DDPG
DDPG 作为一种比较成功的 AC 类算法,已经在很多任务中取得了不俗的表现。但它有一个致命的短板,就是 overestimation 的问题,容易造成 policy 收敛困难。最典型的就是在 gym 的 BipedalWalker 中,如果采用原始的 DDPG 算法,是很难 solve 的,你会发现你的总奖励值始终卡在很低的水平,根本无法进步。这里的主要原因就是对 Q value 的过高估计,导致 agent 一直在糟糕的策略下挣扎,无法找到有效的策略。
为了解决这个问题,TD3 横空出世。它其实就是 DDPG 的升级版,网络架构跟原版基本类似,但是它参考了 Double DQN 里面双 Q 网络的设计,采用了两个 Critic 网络,在计算 Q 值估计时,会让两个网络分别去预测,然后取最小的那个值。这里其实就是经典的双学习思想,具体的原理在 Sutton 的书里有详细讲解。
核心设计
1. Twin :双 Critic 网络
DDPG 在训练过程中容易出现 over estimation 的问题,即对 Q value 的估计偏高,而且这种 bias 会随时间积累,导致算法无法收敛。
This is caused by the algorithm continuously over estimating the Q values of the critic (value) network. These estimation errors build up over time and can lead to the agent falling into a local optima or experience catastrophic forgetting
针对这个问题,提出了 DDPG 的改进版本,即TD3 ,它参考了 DQN 中 Double Q-learning 的设计,在原有的架构上使用了两个 Critic 网络。
而 DDPG 原有的 target 网络虽然也是从 DQN 的设计中演化来的,但 target 网络对于解决 over estimation 并不理想,因为
This is because the policy and target networks are updated so slowly that they look very similar
但为了稳定更新的目的,Target 网络还是需要保留,所以 TD3 实际上采用了两套 Critic 网络,Local 网络和Target 网络都包含两个独立的 Q network。
-
每次更新,取两个 Q target 网络中对 Q value 估计值较小的那个作为 Q 目标
\(Q_{target} = min [ Q_{\theta'1}(s',a'),Q_{\theta'2}(s',a') ]\)
-
critic 的总 loss 计算: 把两个 local 网络的 MSE 误差相加
\(Loss = MSE(Q_{\theta1},Q_{target}) + MSE(Q_{\theta2},Q_{target})\)
2. Delayed:延迟更新策略
在 Actor-Critic 架构中使用 Target 网络,虽然能起到稳定训练的作用,但也可能会引起一个严重的问题。如果一个糟糕的策略被错误的过高估计 (overestimated) ,那么这个错误就会持续累积,导致策略网络无法收敛 diverges。
解决办法就是对 Policy 使用延迟更新的方法,让 Policy 更新的频率比 Critic 更低,这样就可以让 Critic 有足够的时间稳定 Q 函数并纠正错误,避免错误的估计影响策略更新。
TD3 uses a delayed update of the actor network, only updating it every 2 time steps instead of after each time step, resulting in more stable and efficient training.
- 每个 time step,Critic 都更新一次;而 Actor 则是每隔 N 个 time step 才更新一次
3. Noise Regularisation
确定性策略有个缺陷,在更新 Critic 的时候容易产生高方差的 Q value 估计。
his is caused by overfitting to spikes in the value estimate.
TD3 采用了一种正则化方法,__目标策略平滑 __(target policy smoothing).
在计算 Q 目标时,给 action 加入一个小的随机噪音,并采用截断 (clipped noise)来避免过多的偏离原始值,经过多个 mini batch 的累加,这些噪声会取得近似的平均。
加入了噪声后,对于那些更 robust 的动作(对于噪声和干扰的抵抗力更强),Critic 就能给出更高的 Q value,从而让 policy 更稳定。
算法流程
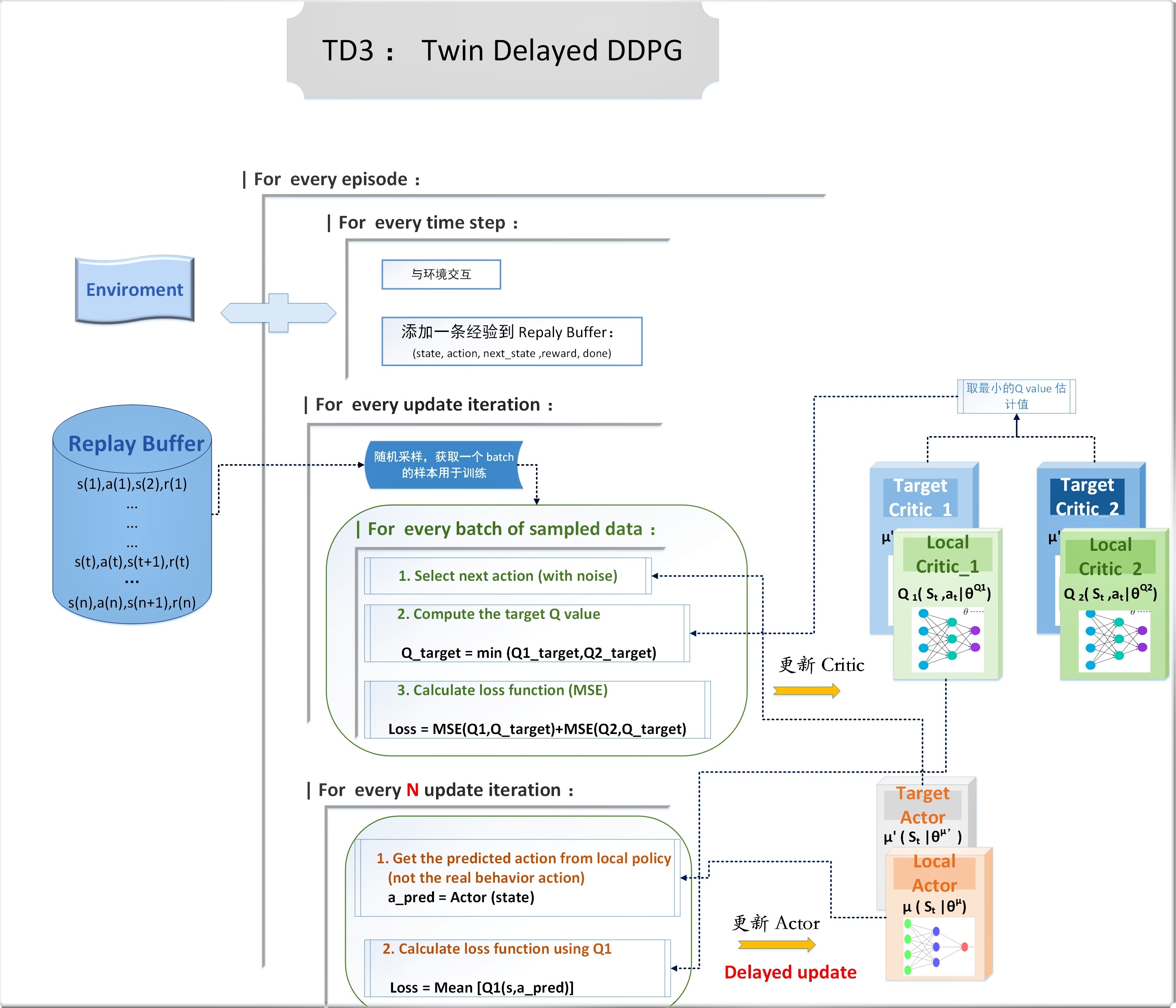
TD3 伪代码




 浙公网安备 33010602011771号
浙公网安备 33010602011771号