经验紧束缚法、实空间紧束缚法
经验紧束缚法是在下面资料中确有其名,但"实空间紧束缚法"这个名字是我自己编的。两种方法的结果其实等价。
一、经验紧束缚法资料
经验紧束缚法:
赵明文. 材料计算中的紧束缚方法[OL]. (2020-08-18). https://www.koushare.com/video/videodetail/6335 (非常推荐,感谢赵老师)
Hergert的Group Theory in Solid State Physics and Photonics书第九章(非常推荐)
peter yv的半导体物理书
martin的电子结构书。虽然写得不友好,但其中推荐了很多紧束缚方面的书、文献、综述等,学会了就行
slater-koster参量法:
对 s,p, d 轨道: J. C. Slater and G. F. Koster, Phys. Rev. 94, 1498 (1954).
(此 Slater, Koster, 1954 中表1的证明见:Podolskiy, ., and P. Vogl. "Compact Expression for the Angular Dependence of Tight-Binding Hamiltonian Matrix Elements." Physical Review B 69, no. 23 (2004).)
对 f, g 轨道: Sharma, PRB, 19,2813(1979). Podolskiy \& Vogl, PRB, 69,233101(2004).
原子轨道学习:cohen量子力学书卷一、levin量子化学书
推荐重复的文献:
G.-B. Liu, W.-Y. Shan, Y. Yao, W. Yao, and D. Xiao, Physical Review B 88 (2013).(非常推荐,前提是学一下李新征群论书第四章。通过群论分析及与第一性原理计算的能带结果进行拟合得到hopping参数)
Z. Zhong, Q. Zhang, and K. Held, Phys. Rev. B 88, 125401 (2013).(非常推荐,感谢up主在 https://www.bilibili.com/read/cv9005579?from=search&spm_id_from=333.337.0.0 中推荐的此篇论文。此论文介绍了两种得到hopping参数的方法,一种是wannier90直接得到,一种也是通过群论分析及与第一性原理计算的能带结果进行拟合)
二、G.-B. Liu,Physical Review B 88 (2013)论文中(2)(3)式的证明:


三、听赵明文老师在蔻享的材料计算中的紧束缚方法课记的笔记 (经验紧束缚法)

从头算方法:像高铁
紧束缚方法:像马车。它虽然没有高铁快,但是能在沿途中发现高铁发现不了的东西。紧束缚方法有从头算不可替代的价值

(hubbard模型即电子-电子相互作用有关,加电场磁场可以调控能带(利用皮尔斯替换可以考虑磁场的效应),考虑自旋轨道耦合可以研究拓扑,可以研究力学的strain(因为跳跃积分是和两个原子之间的距离等是相关的)、加周期性的光场(也是通过皮尔斯替换来研究)(可以研究激光诱导下紧束缚模型能带的变化),)
紧束缚方法这个马车可以承载很多物理,它不能替代高铁,但是有它本身的价值
1 紧束缚方法的基本原理
 (从布洛赫定理引入了k)
(从布洛赫定理引入了k)

平面波方法:见李正中书或一些固体物理书。用平面波来展开:
 (可以验证其满足布洛赫定理)
(可以验证其满足布洛赫定理)
由于它是正交完备的,所以包含的平面波的数目越多,计算越准确。(从vasp就知道,即截断能越高,计算越准确,但计算量越大)。
平面波法的缺点:平面波是非定域的,要叠加成定域的波包等,则所需要的平面波就很多,计算量很大
另一种方法:
原子轨道线性组合法的过程:(这些计算过程的来源应该是来自计算物理课件解偏微分方程的基展开法,过程完全一样!紧束缚方法最早应该是来源于数学中的基展开法)

若每个原胞中只有一个原子轨道:
验证时应该用来验证
(也即倒空间周期函数按正格矢傅里叶展开)
固体物理书中最后得到:
若每个原胞中包含多个原子轨道:
出现这种情况,有两种可能:
- 一个原胞中包含多个原子,即复式格子,即基元有多个原子。若每个原子有一个原子轨道,则这样原胞中就有多个原子轨道。
- 一个原胞有一个原子,但这个原子需要考虑它的多个原子轨道。
当是第一种可能时,这是一个复式格子,对每个原胞中的每个子格的每个原子轨道作“布洛赫和”(即前面说的倒空间周期函数按正格矢傅里叶展开),
a.对每一个子晶格 每一种原子轨道() 做Bloch 和, 形成 个 Bloch函数:
 (1.1)
(1.1)
特别注意,从于鑫半导体物理书(2.74)知【我仔细验证过(2.74)】,(1.1)错误,正确的公式应为:
【注意e指数上的+号】
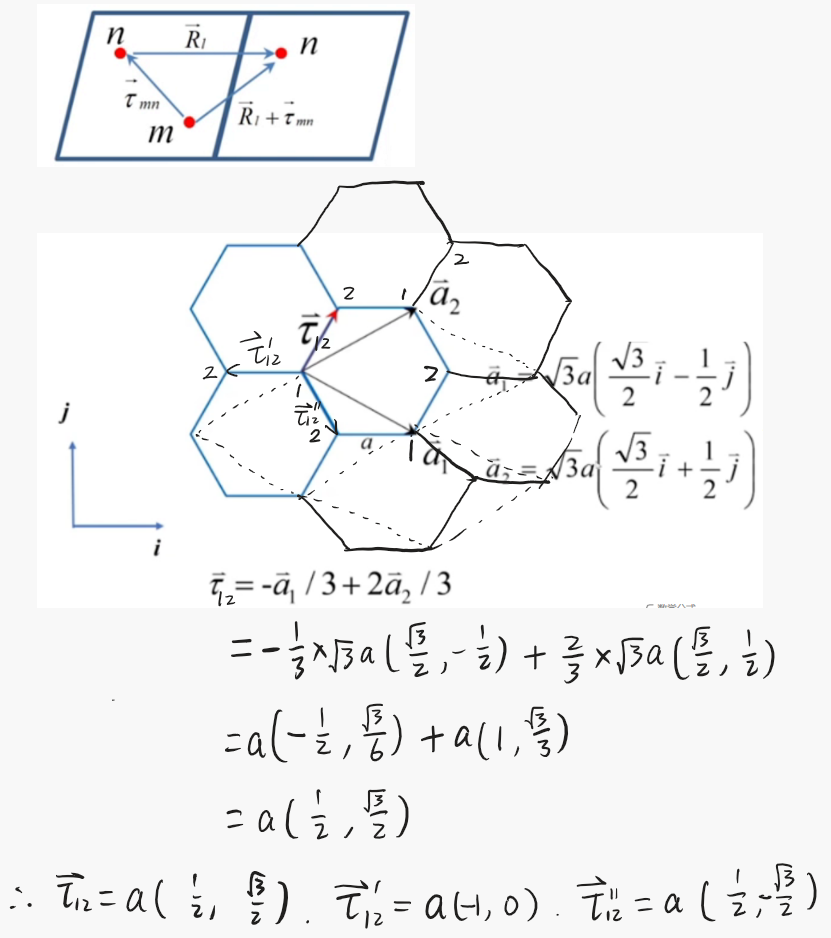
其中是第个原胞的位置,是每个原胞中第个原子在原胞中相对位置。
将这些 Bloch 函数重新编号, 记为:
b.把晶体中电子的波函数表示成上述基函数的线性组合:
因为这些布洛赫基函数都满足布洛赫定理
,故线性组合后得到的也满足布洛赫定理。
其实这就是计算物理课中讲的基展开法求偏微分方程的解!计算物理课件中也是下面这样的推导过程,而且也说了这是LCAO方法。利用下面的推导过程,就将一个偏微分方程转化为一个线性代数方程组。
将以上线性组合(1.2)代入,并左乘,并积分,就是将微分方程转化为了线性代数方程组:
其中,是哈密顿量在“布洛赫和”中的矩阵元,是“布洛赫和”的交叠积分矩阵元。(若使用Lowdin方法构造的原子轨道,则Lowdin原子轨道构成的布洛赫和是正交归一的,则此时,具体见slater1954年论文1500和1501页,还可以证明Lowdin原子轨道与原来的原子轨道有相同的对称性,也见slater1954年论文1501页)
从(1.3),得:
解久期方程就得到能带
c.计算哈密顿量矩阵元
计算哈密顿量矩阵元有很多困难,其中,
单电子受到的势场可以表示为所有原子的势场的叠加:
 (1.6)
(1.6)
将(1.2)和(1.6)代入(1.5),会发现会面临多中心积分的问题:
后一个公式中有三个指标,故称为多中心积分
特别是计算三中心积分,会遇到很多困难。
在紧束缚方法中,有解决多中心积分问题的一个方法:
参量化方法和原子轨道相互作用模型:
将哈密顿量矩阵根据原子轨道的不同而进行分类:
s轨道:
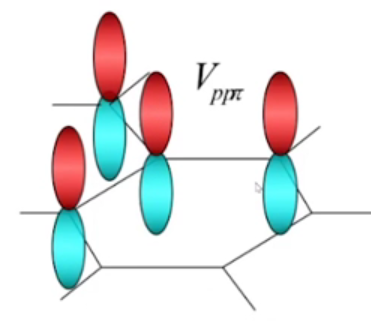
p轨道:各向异性:分别Py、Px、Pz:
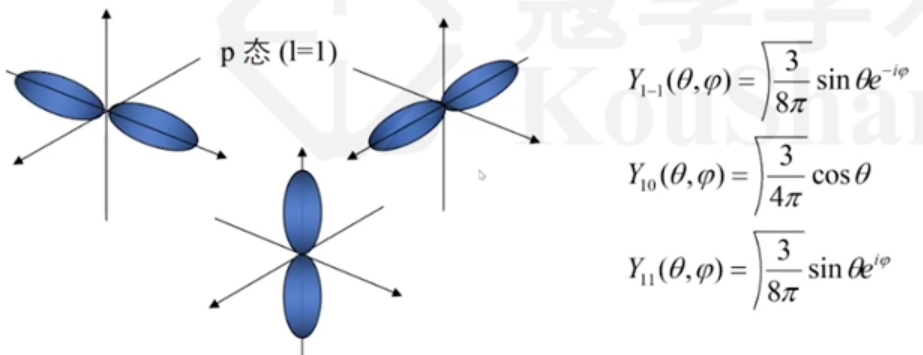
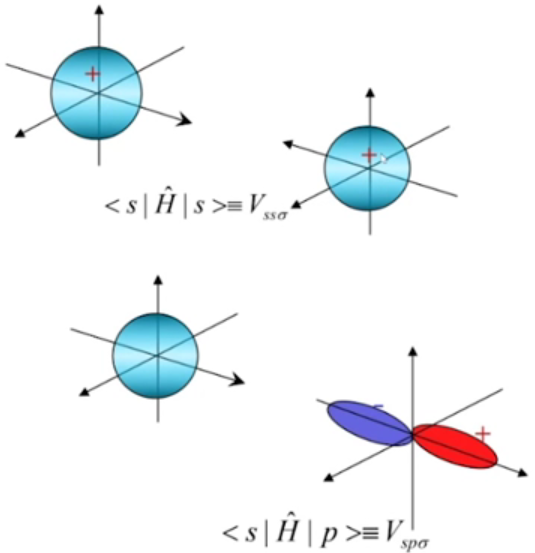
(第一个图中中的是表示两个波函数交叠的形式是以来交叠的)(第二个图中p是轨道)
好像是化学中的键来命名
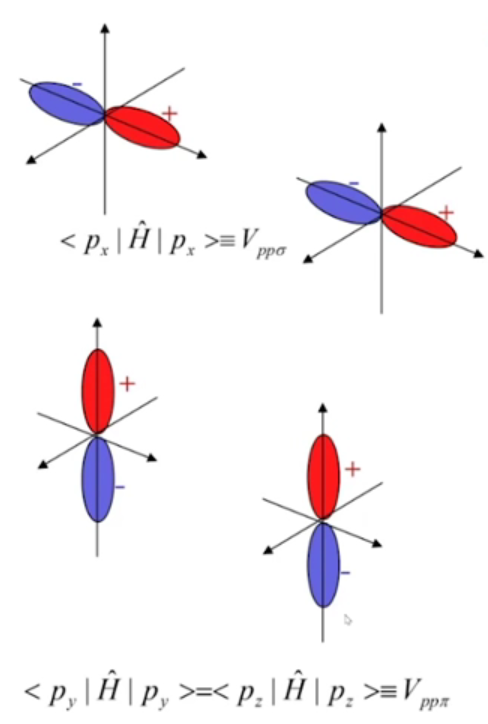
以上都是特殊情况,更一般的情况:
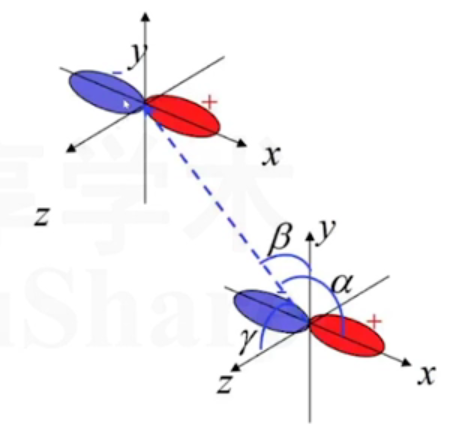
如图,设两者之间的位置矢量在x方向的夹角为,在y方向的夹角为,在z方向的夹角为. 此时两者之间的交叠既有的成分,也有的成分,
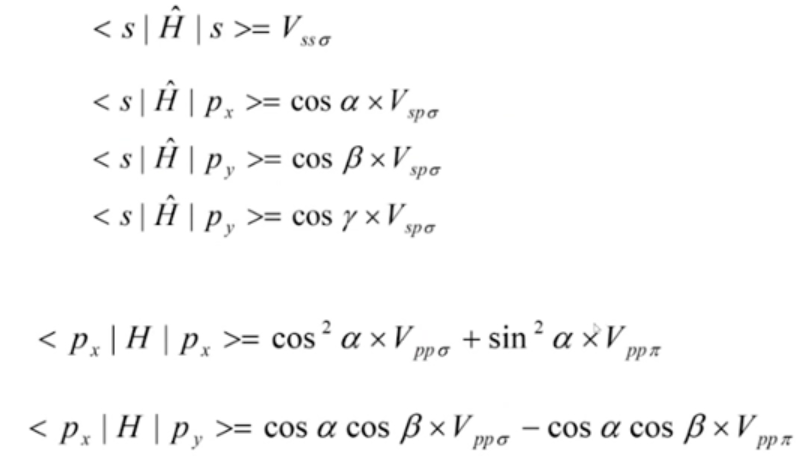 (1.6)
(1.6)
这样就将任意情况的哈密顿量矩阵元用等表示出来了。
以上公式是怎么得到的?为什么有?
这些未知的等的求解方法就是用实验数据来对比或用高精度的第一性原理计算结果来对比得到。
以上是s轨道、p轨道的情况,若有d轨道参与的情况,可以从资料上查到参量化关系。
接下来就可以得到哈密顿量矩阵元:
图中原子轨道分别在n位置和m位置:
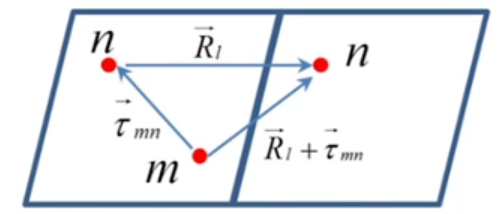
类似peter yv半导体物理书88页(2.78)的证明过程或2013三能带二硫化物的论文G.-B. Liu,Physical Review B 88 (2013)中(3)的证明过程,知:
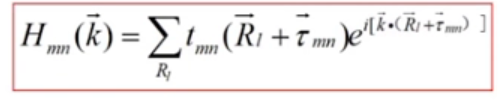 (1.7)
(1.7)
重要:(1.7)的具体证明及tmn的具体公式见Hergert的mma群论书211页,很严谨!!!:




【但以上公式存在错误,正确的公式见peter yv半导体物理书(2.74):




】
2013紧束缚论文G.-B. Liu,Physical Review B 88 (2013)中的公式(2)-(5):

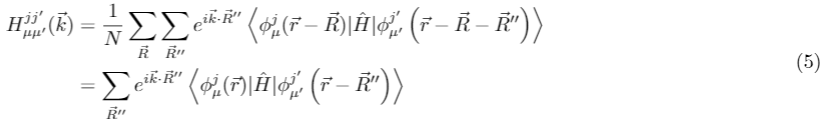
并没有错误!虽然与Hergert的mma群论书211页(9.31)不同,这是因为2013论文G.-B. Liu,Physical Review B 88 (2013)中是基元只有一个原子的情况,此时Hergert的mma群论书211页(9.31)自然就化为了这里的2013论文G.-B. Liu,Physical Review B 88 (2013)(5)。
d.解久期方程得到能带和本征矢:
得到了矩阵元,根据(1.4)求出能带和本征矢。一个对应一个本征矢,故:
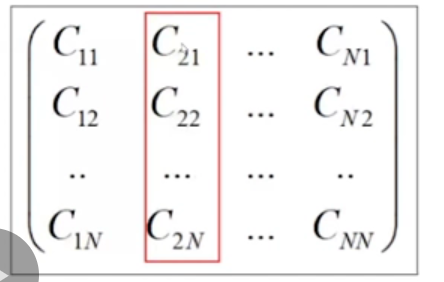
得到了系数,再根据(1.2)就能得到单电子波函数。
有了单电子波函数,就可以去求拓扑等性质,比如拓扑不变量,其实思路类似我的笔记“SSH模型”。
2 紧束缚方法在低维体系中的应用
石墨烯(这是一种和bernevig书中紧束缚方法不同的方法,但结果竟然一样)
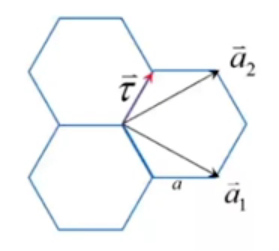
复式格子,每个原胞中两个原子,假设每个原胞中每个原子只考虑其轨道,如图:
则每个原胞中有两个原子轨道。
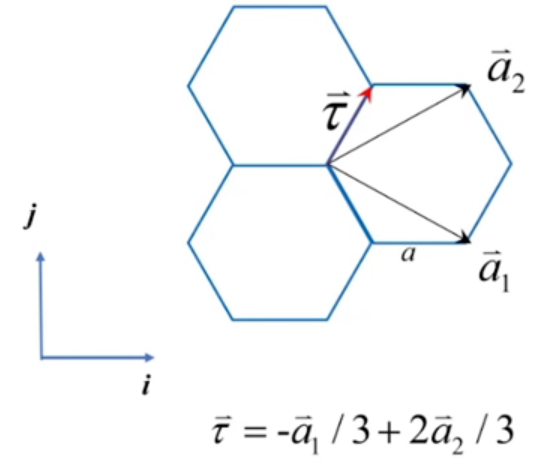
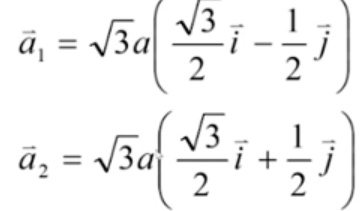 ,其中两个子格的相对位置就是 .
,其中两个子格的相对位置就是 .
两个子格的布洛赫和分别为:
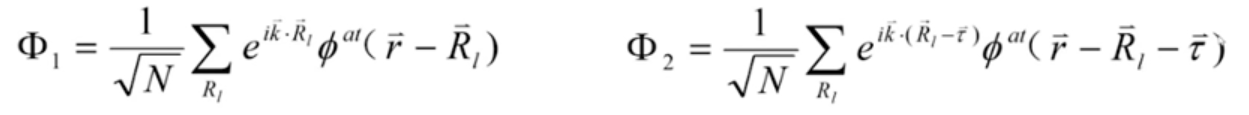
根据(1.4),其久期方程:
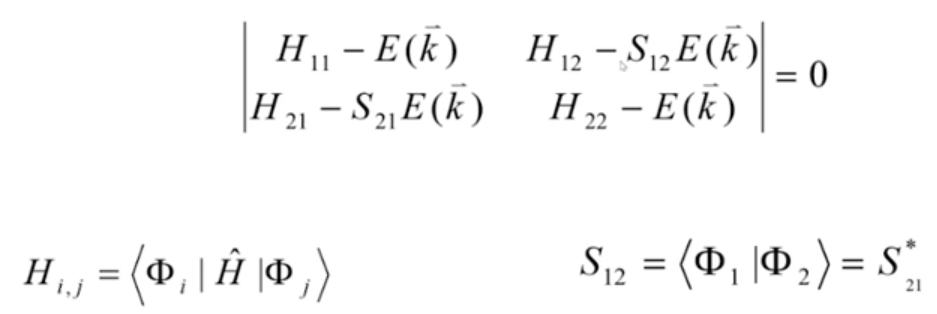
因为哈密顿量是厄米的,故哈密顿量矩阵会有一个共轭关系。
下面求一个哈密顿量矩阵元的例子:
因为紧束缚模型中波函数几乎是定域的,故当时,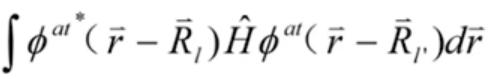 很小,故此积分可以只考虑的情况,故以上公式成立。
很小,故此积分可以只考虑的情况,故以上公式成立。
其中on-site energy: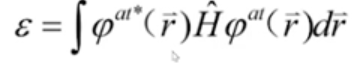 (通过在积分中变量代换等可以知道,此式确实成立)
(通过在积分中变量代换等可以知道,此式确实成立)
在位能到物理意义:一个电子在格点上时的能量。
下面求交叠积分:根据(1.3)后一句话,有:
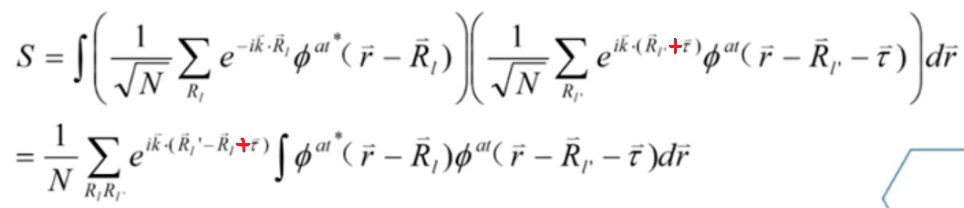
若只考虑最近邻的交叠积分,忽略次近邻以外的交叠积分,则:
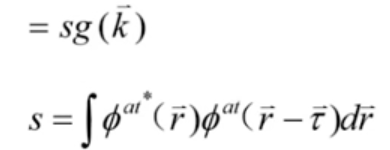
其中:“相位”: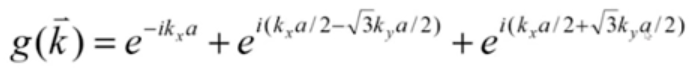
虽然这里得到了S交叠矩阵,但在后面说了,后面又进行了一个近似,近似认为S交叠矩阵等于0
下面求非对角哈密顿量矩阵元:
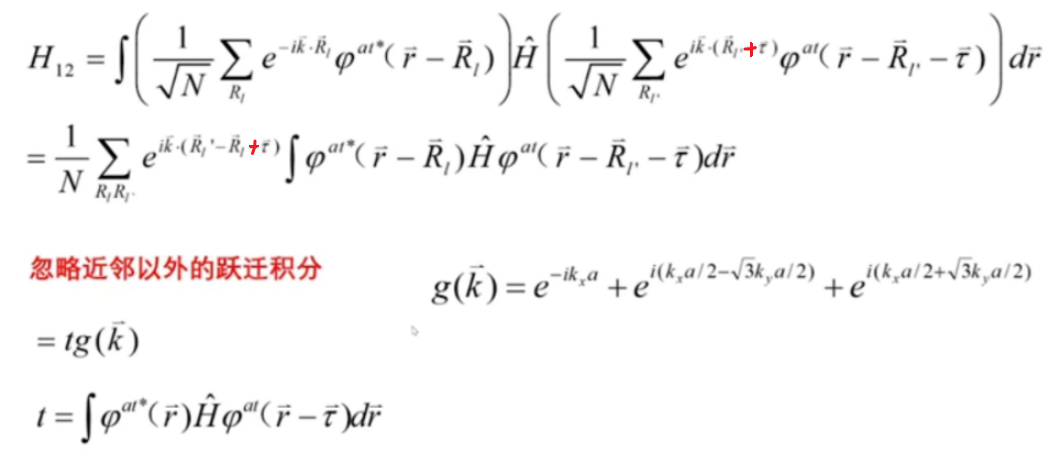
推导过程:
解久期方程得能带:
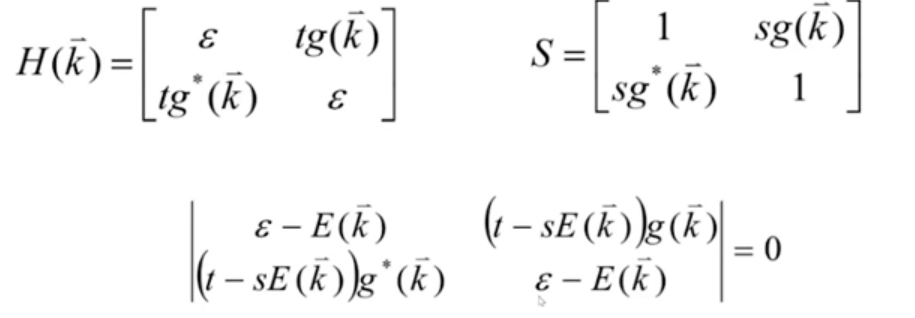 (1.8)
(1.8)
一般来说,我们可以将在位能取为0,若我们再忽略交叠积分S矩阵(含义就是认为不同原子轨道对应的“布洛赫和”是正交的),则:
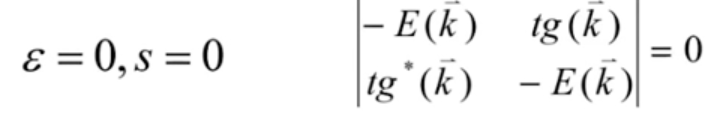
根据s的表达式
,其实也就是认为不同格点的轨道波函数相互正交。我曾疑惑,若这里认为不同格点的轨道波函数正交,则不是就波函数没有重叠,则就没有hopping吗? 但实际上在重叠积分那里只是近似
=0而已,而实际上在跃迁项那里,H12和H21就不等于0,即
不等于0.
特别注意,在阎固体物理书中紧束缚一节,也完全是这样假设的:,而后面在hopping积分那里就写的不为0:
此时解得:有两个解,故有两个能带: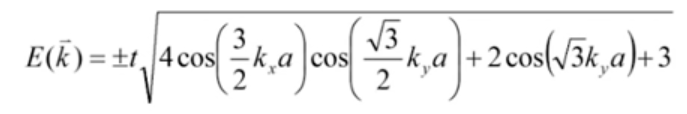
石墨烯倒格子:
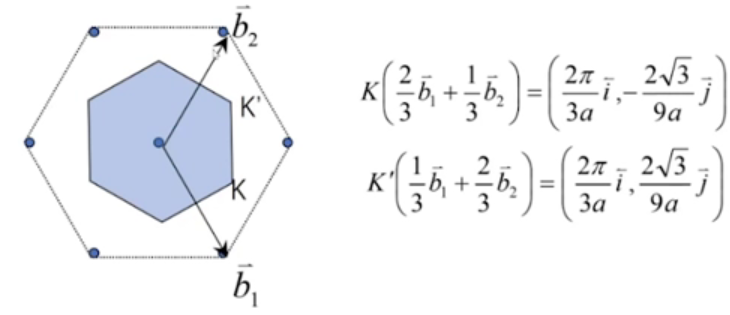
其中阴影区域就是石墨烯1.BZ。
将K和K'坐标代入上面能带表达式,得: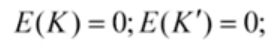
对能带表达式泰勒展开:

从(1.8)可以知道,在狄拉克点附近,有效的低能哈密顿量:
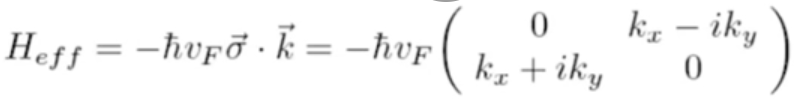
相当于狄拉克方程: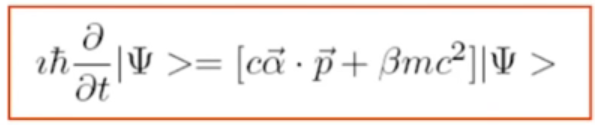 中质量项m=0,即零质量狄拉克费米子
中质量项m=0,即零质量狄拉克费米子
氮化硼
氮化硼又称白石墨;另一类是碳化硅。它们都是形成六角类似石墨烯的结构,只不过原子一个是碳,一个是硼:
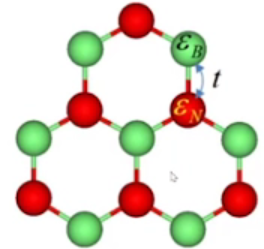
和上面石墨烯的方法类似。唯一不同的是,硼原子的在位能和N原子的在位能是不相等的,而石墨烯中两个原子在位能相同从而可以取为0,故:
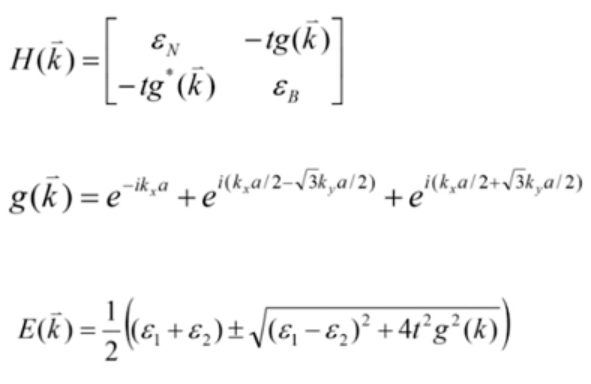
可以发现,在和附近,能带:
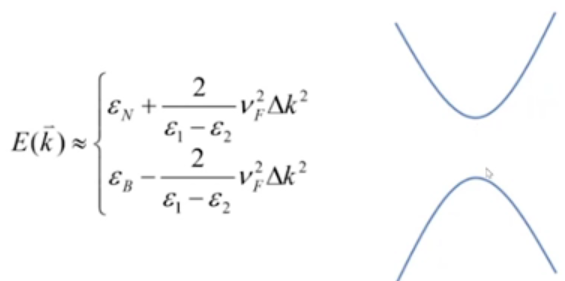 这也是泰勒展开得到的。
这也是泰勒展开得到的。
在和附近,可以发现是抛物色散关系,而且有能隙,能隙是硼和氮的在位能之差。
不过当然这种材料用从头算方法也能很容易算出这种色散关系。
类石墨烯
原胞比石墨烯更大,包括6个碳和两个硅:
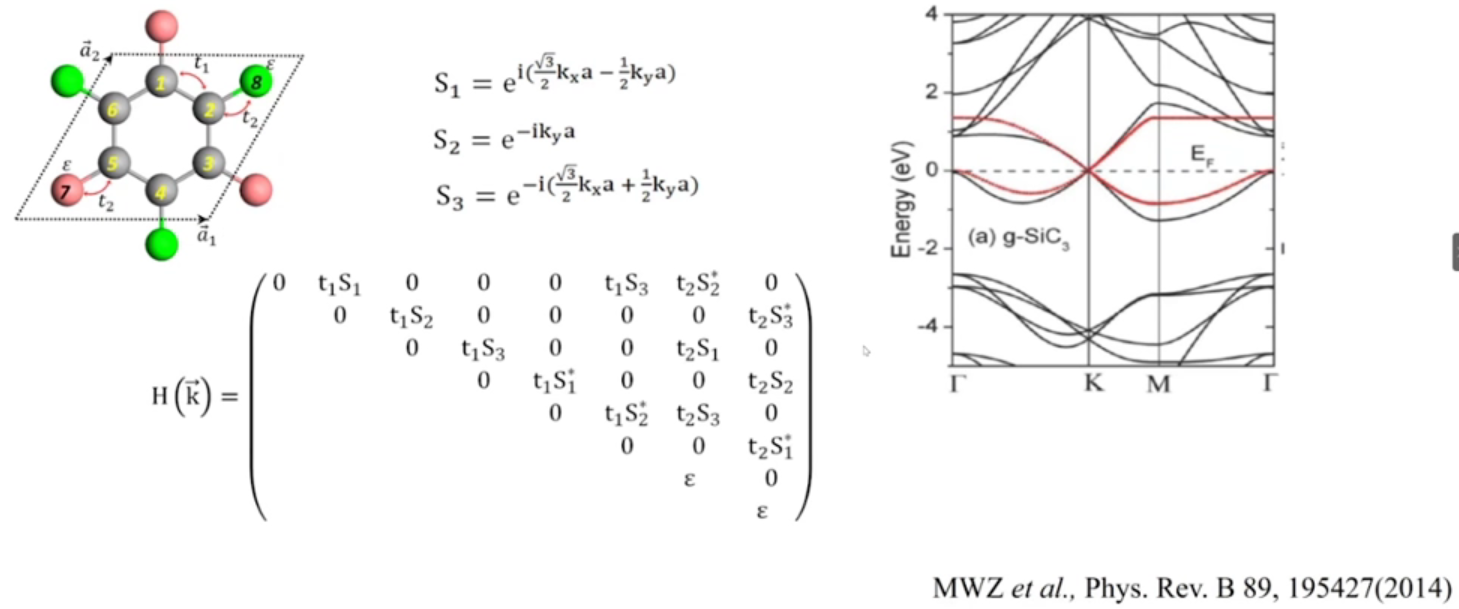
原来以为,因为碳和硅的在位能不同,这里会不会打开一个带隙,但计算发现,在K点没有带隙。
所以在二元的类石墨烯结构中也可能存在一个狄拉克锥。
后来实验合成了和,计算发现,的狄拉克锥位于导带,的狄拉克锥位于价带。
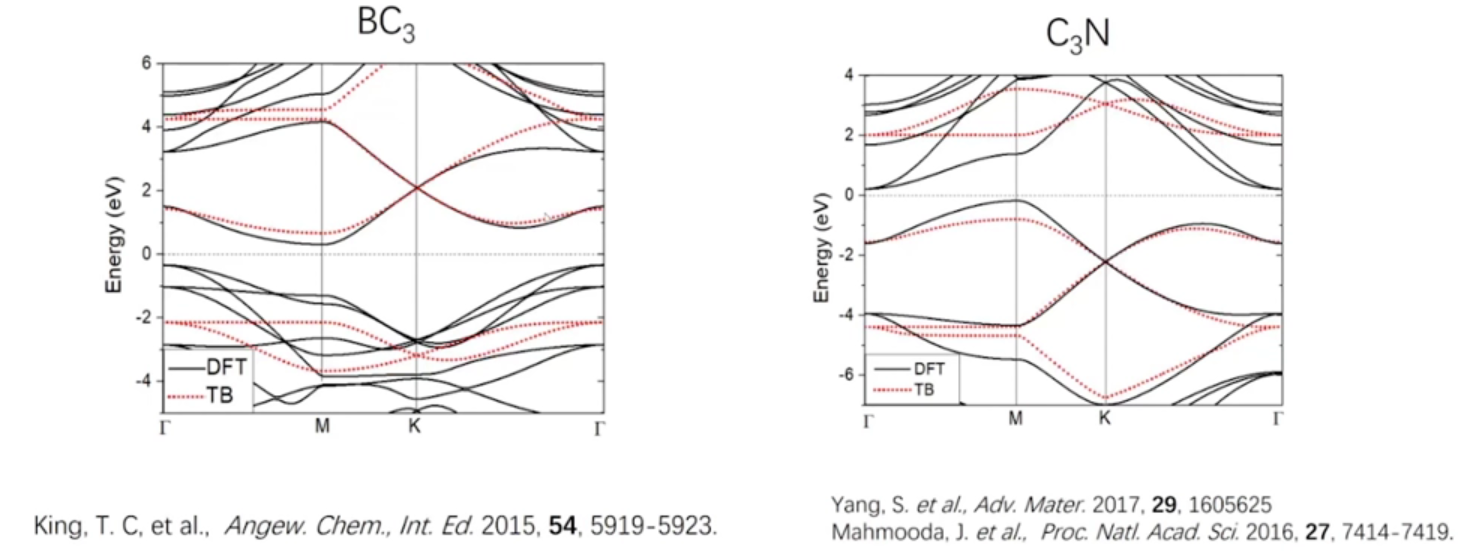
DFT方法和紧束缚方法的计算结果符合得很好。
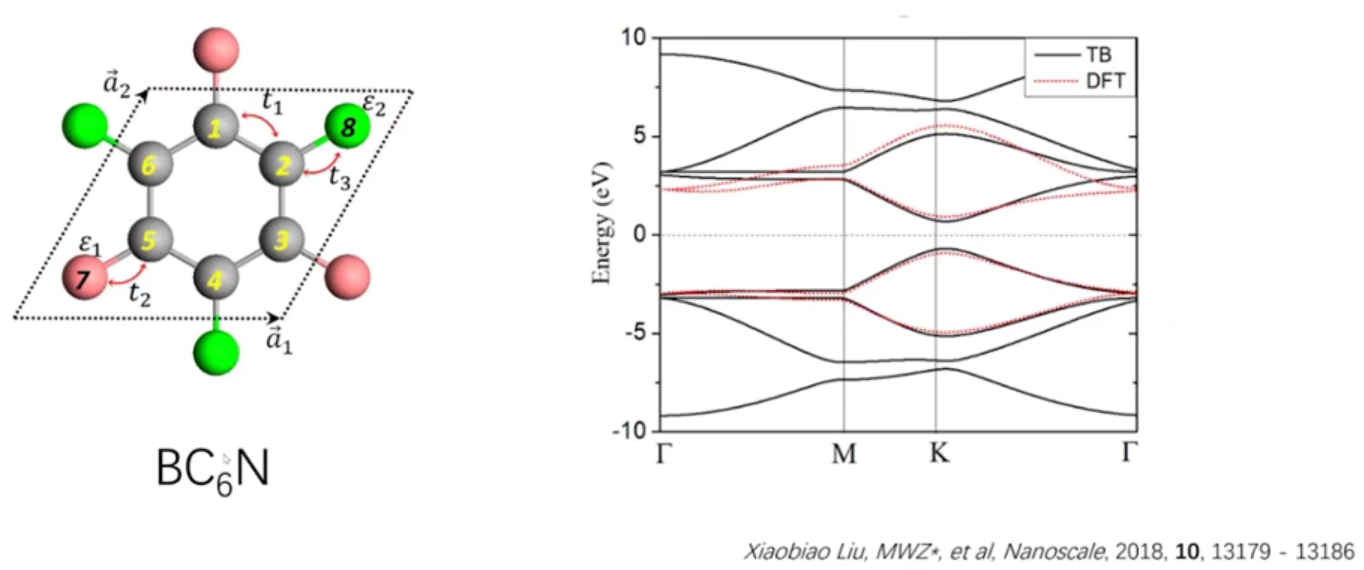
这种情况破坏了体系的中心反演对称,此时打开了一个带隙。
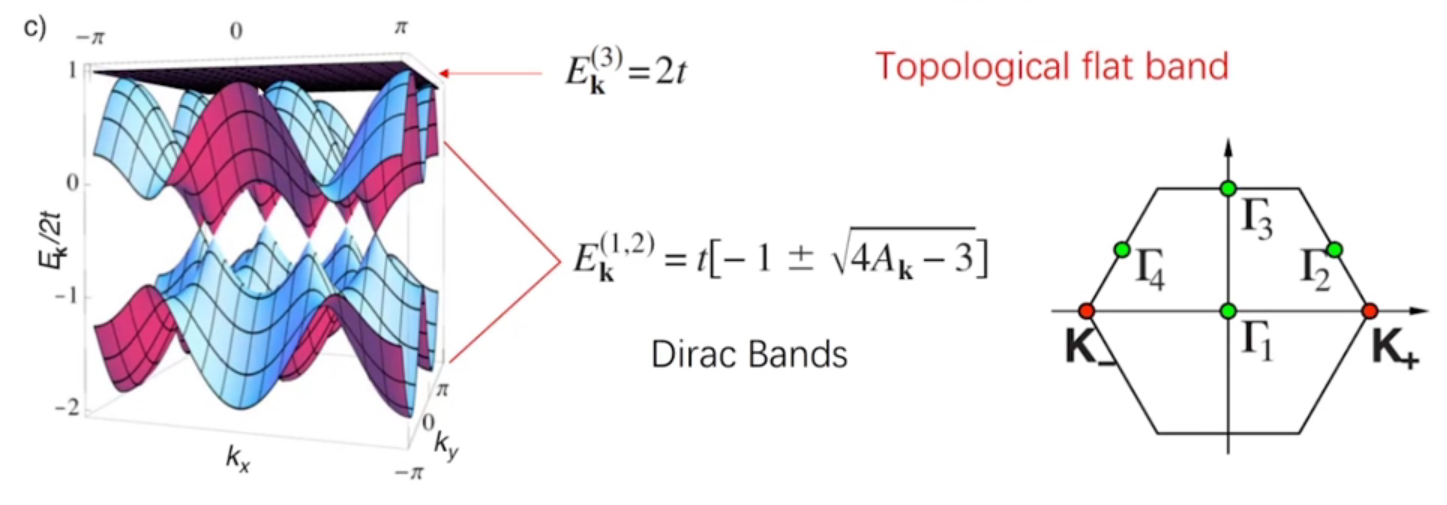
Kagome晶格
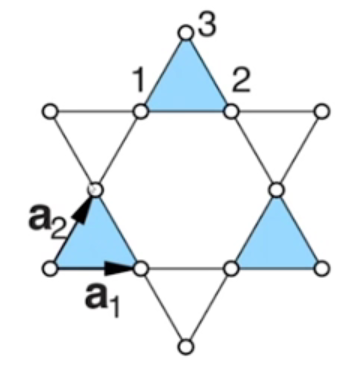
每个格点都放一个原子时,就构成了一个kagome晶格。kagome晶格中每个原胞中包含3个原子,其原胞为:
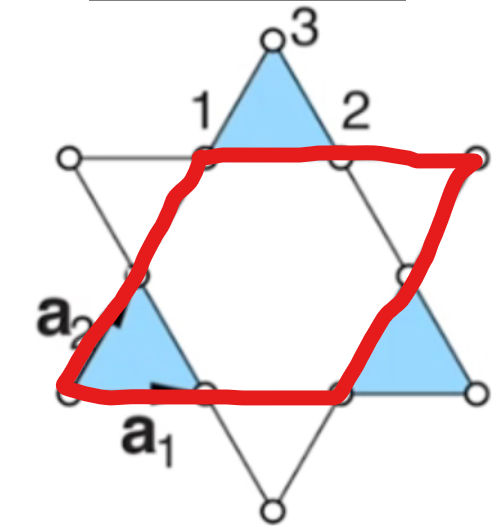 红线就是原胞。
红线就是原胞。
若每个原子上只考虑一个原子轨道,...可以解析解得到其能带:
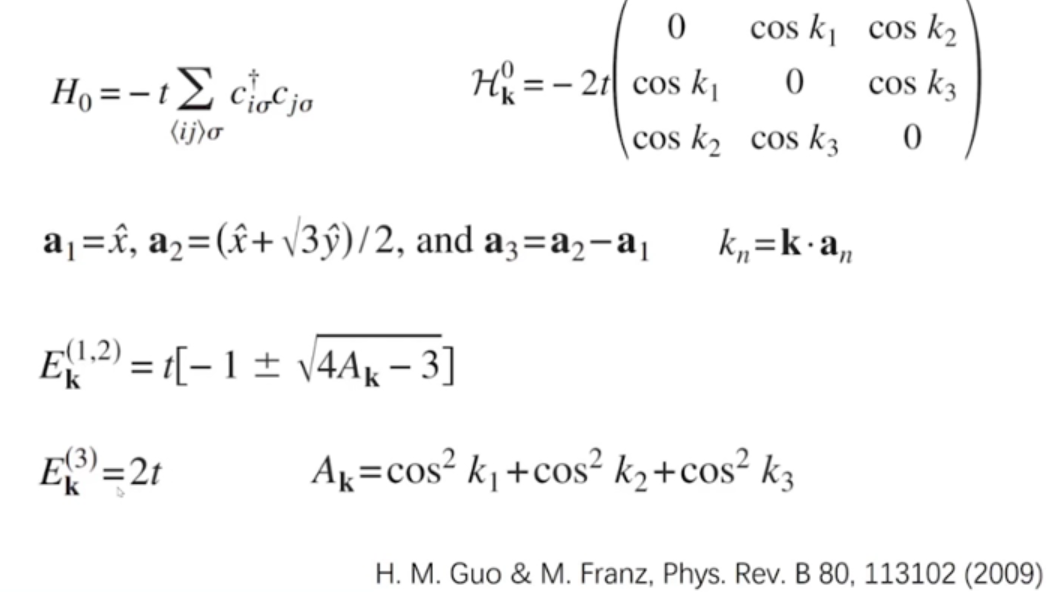
3个能带,两个与k有关,一个与k无关,即平带
平带就是一个完全无色散的能带,可以证明在平带,就是范霍夫奇点。
在一般的半导体中,说到平带,一般就是缺陷态,比如黄昆固体物理书半导体物理一章中说了,杂质能级就是能隙中的一个能级。
对缺陷态来说,电子是局域的,其能带就是一个平带。但在kagome格子中上面这个情况,解的情况是,电子的波函数是非定域的,而此平带出现原因是“几何阻挫”,称为“拓扑平带”,此平带中电子的关联性很强,因为平带相当于电子的动能为0,则其势能(电子-电子相互作用)的效果就很强。
最早是在金属有机体系中发现有kagome晶格的能带特点的材料(虽然材料的实际晶体结构不是kagome晶格):
拜占庭晶格

每个原胞有6个格点,每个格点一个原子轨道,也可以写出其哈密顿量,最后发现有狄拉克锥
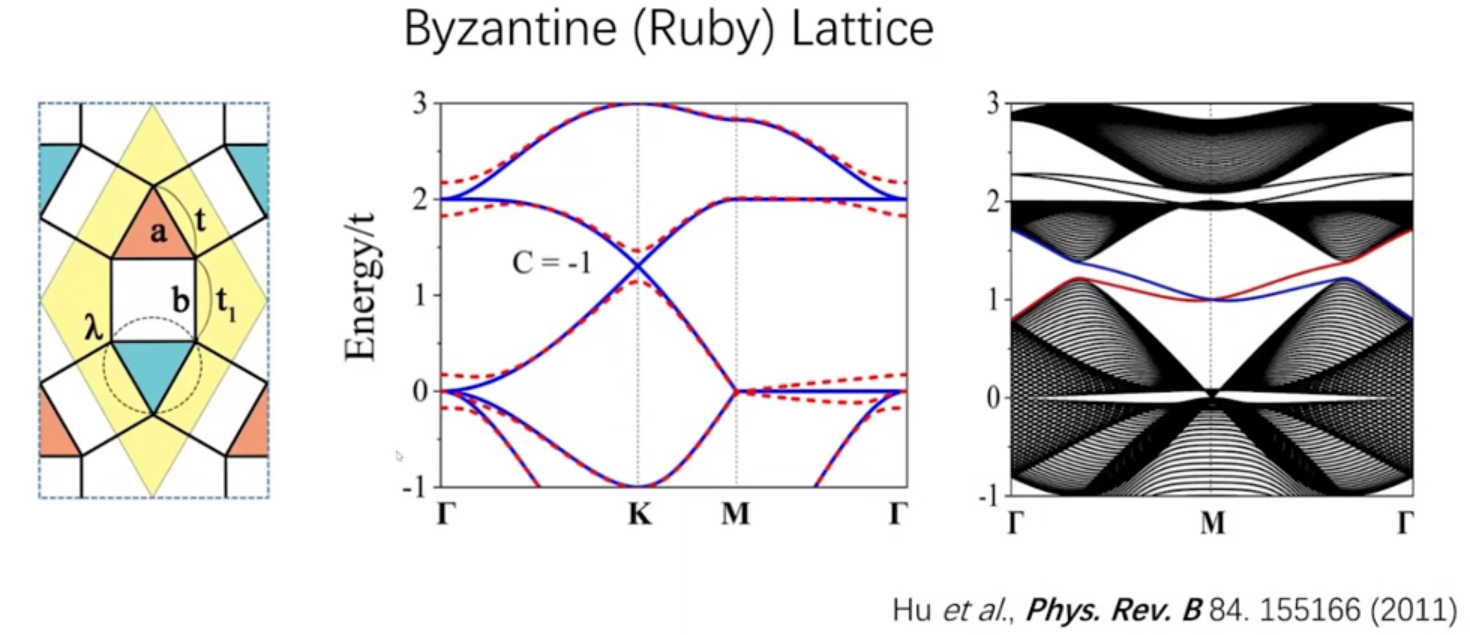
实验发现这种材料,经过理论计算发现,其能带是拜占庭晶格类型的能带:
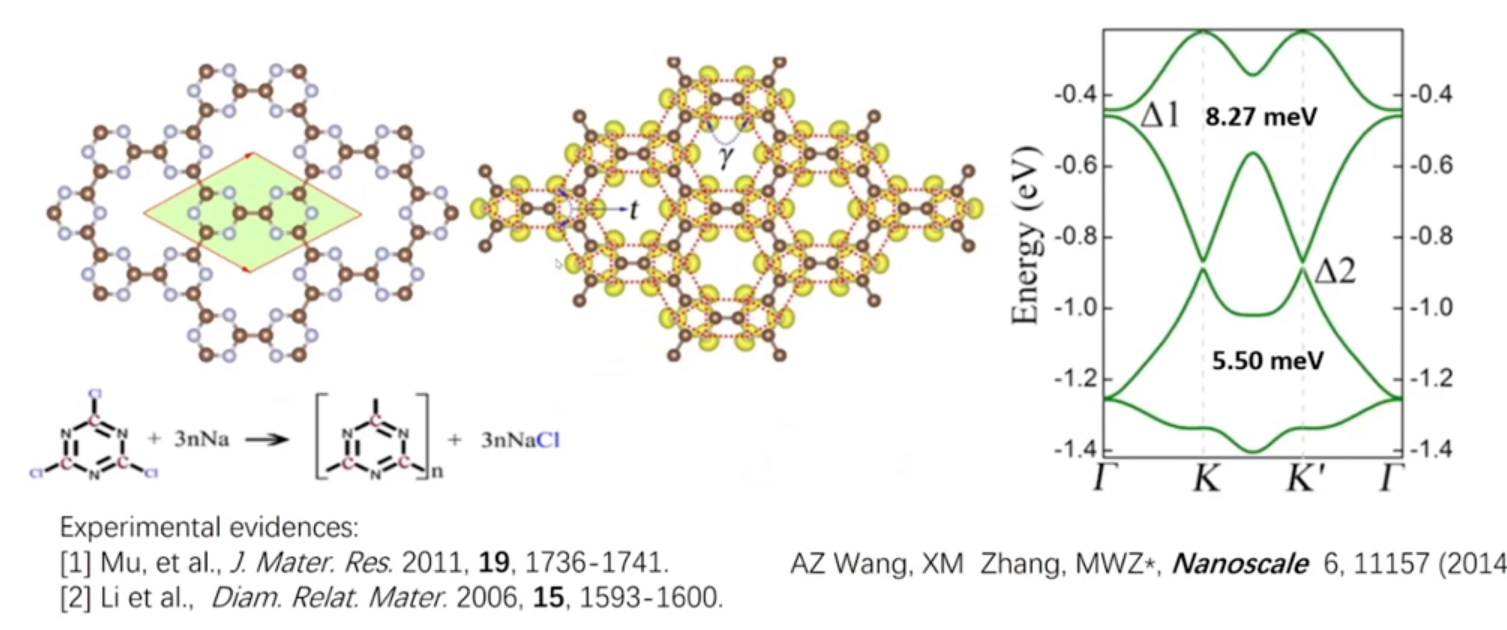
!紧束缚方法的价值、特点
综上,紧束缚方法是很灵活的,紧束缚方法是基于原子轨道的分布,而不是基于原子的分布,因为有些原子可能对附近的态没有贡献
在很多复杂的结构中,费米面附近的态的来源可能只来源于部分的原子,比如材料,费米面附近的态来源于氮原子,可以发现其能带结构的特征是拜占庭晶格的能带的特征,而从其实际的晶体结构中发现不了它是拜占庭晶格的特征,这是因为只有某些原子对费米面附近的态有贡献,而不是整个晶体结构的原子。
一维碳纳米管
石墨烯边缘切的方向不同,所形成的碳纳米管的手性就不同
碳纳米管的结构非常丰富,有很多种,而且其电子结构
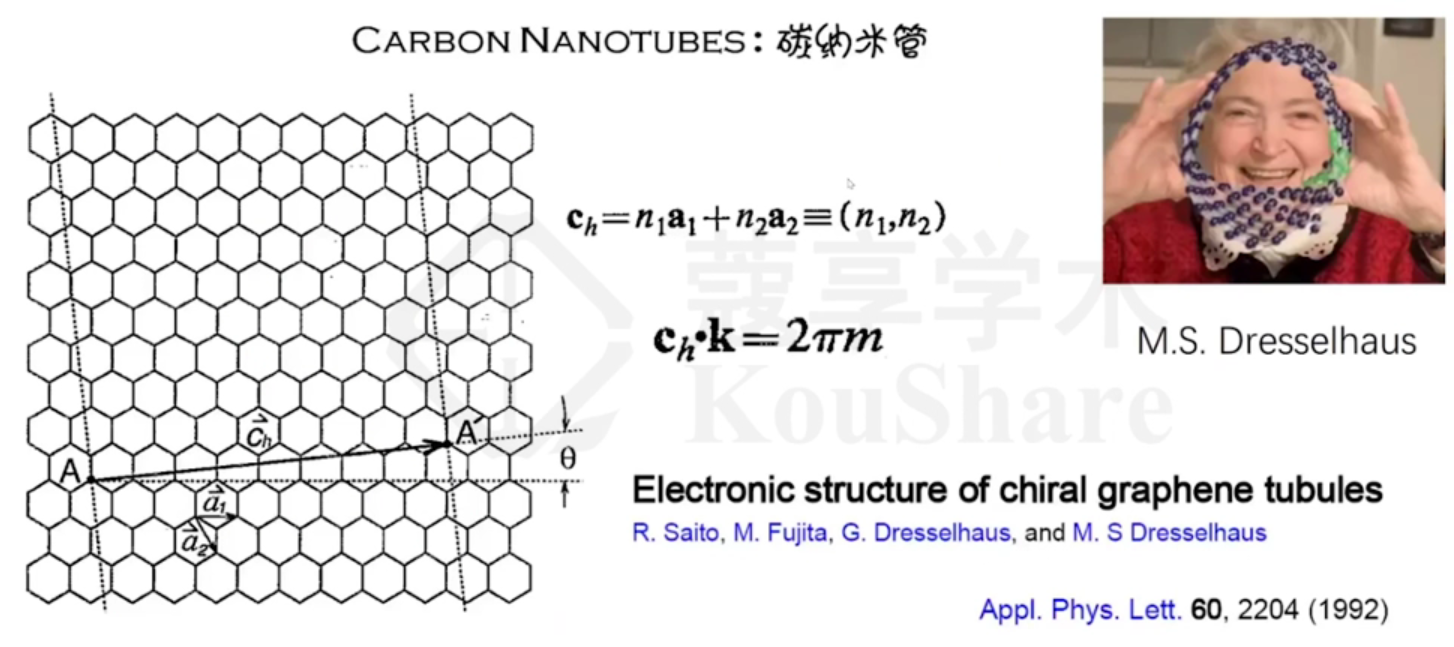
在50多分钟到1小时这段时间在讲怎么求碳纳米管的电子结构,我没听,以后再说
紧束缚模型处理电子-电子相互作用
hubbard模型
没时间,以后再说,在1小时
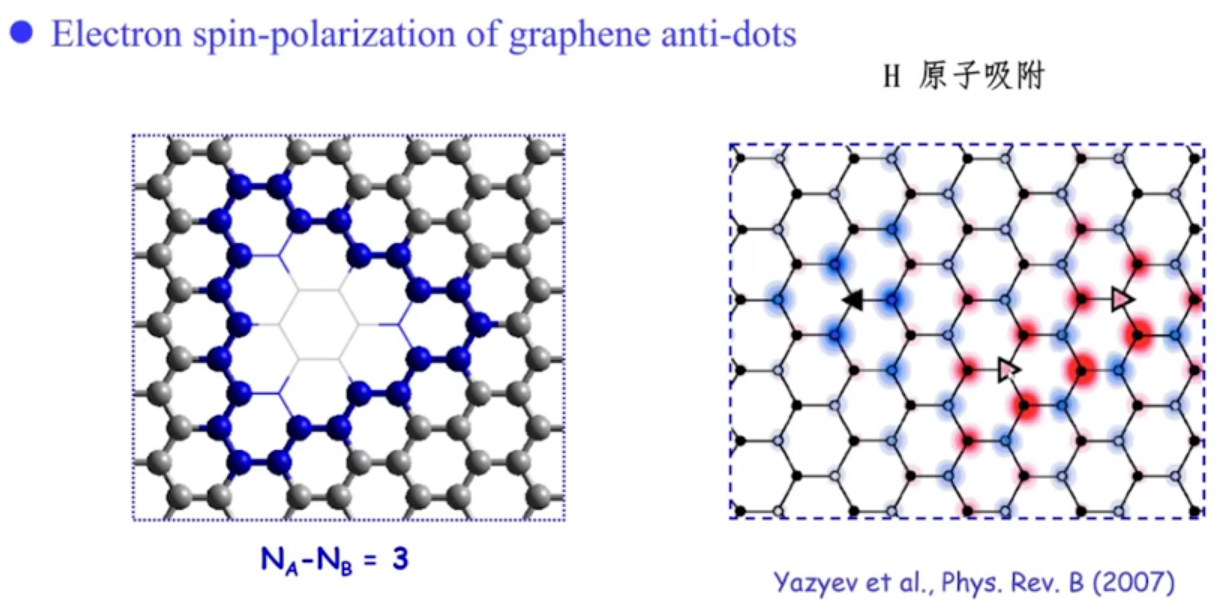
量子点和反量子点的自旋极化、石墨烯纳米螺旋(DNA结构)
实验也验证了!
Kane费米子的有机版本
有机物
参考文献
赵明文. 材料计算中的紧束缚方法[OL]. (2020-08-18). https://www.koushare.com/video/videodetail/6335
如果我写的这个笔记涉及对赵老师侵权,可以联系我删除。
四、原胞中有多个原子、原子上有多个轨道情况的经验紧束缚法(Hergert的Group Theory in Solid State Physics and Photonics书第九章)
参考Hergert的Group Theory in Solid State Physics and Photonics书第九章,严谨,从210页开始:




五、实空间紧束缚哈密顿量法
在 https://iopscience.iop.org/article/10.1088/1361-648X/ab1528/meta 中,给出了从实空间紧束缚哈密顿量到k空间形式的变换,是通过对产生湮灭算符进行傅里叶变换得到的。另外,这篇论文的推导写得非常详细,非常推荐。这篇论文用的不是上面所说的经验紧束缚法,而是另一种也很常见的实空间紧束缚法,bernevig的拓扑绝缘体书中石墨烯那一章就是用的此方法。


此论文中从实空间紧束缚哈密顿量(4)到k空间紧束缚哈密顿量(5)的推导:
从论文fig1知:
其中只取fig1中的P原子格点,或认为取原胞指标。
故:
得证。
经验紧束缚法与实空间紧束缚法其实等价,原因:
在这篇论文中,只考虑了P和B原子上只有一个原子轨道pz的情况。在经验紧束缚法G.-B. Liu, W.-Y. Shan, Y. Yao, W. Yao, and D. Xiao, Physical Review B 88 (2013)论文中,根据
可以求出k空间哈密顿量矩阵元,例如
其中因为考虑最近邻hop,所以对P原子来说,只有onsite能。
故从经验紧束缚法求出来的k空间哈密顿量矩阵元与上面实空间紧束缚法求出来的哈密顿量矩阵元(3)是相同的。故这两种紧束缚法等价。
求hopping参数的两种方法
这篇19年Y Wang et al的论文中用了两种方法求hopping参数,一种是将解析的哈密顿量求出能带再与第一性原理计算的能带用最小二乘法拟合从而求出哈密顿量中的hopping参数,另一种是直接用wannier90得到哈密顿量中的hopping参数,这两种方法其实都挺好,都能复现第一性原理计算的能带,见此论文的fig2:
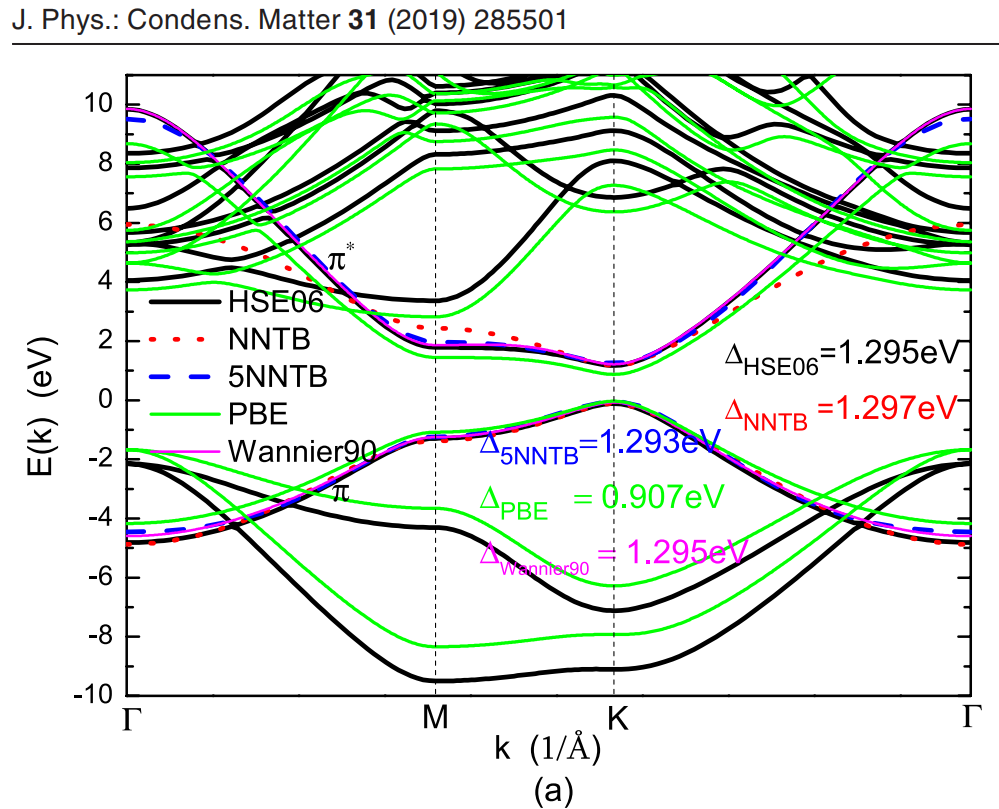
在 S. Fang, etal. Ab initio tight-binding Hamiltonian for transition metal dichalcogenides, Physical Review B, 92 (2015)中提到了通过最小二乘拟合而拟合能带的方法获得hopping参数的方法的缺点:因为拟合能带的方法中有大量参数,在求解过程中,这些参数可能不是独一无二的,且在这种方法中,没有明确地考虑能带的轨道特征或重叠积分的相位,而且可能会发生过拟合。例如,在单层石墨烯的最近邻紧束缚哈密顿量中,在最近跳跃参数t的符号变化下,能带结构是不变的。然而,该跳跃参数的符号可以从光电发射实验中确定。作者发现,他们从利用wannier90构造TBH的程序中得到的符号与Wannier分析一致,但不是从盲目的拟合程序中确定的。在某些情况下,由于过拟合而引起的差异可能会更加微妙。另一个例子是,一项与bi-Sb合金[34]相关的研究指出,有可能得到在表面态描述上不一致的拟合哈密顿量,这是由于错误的镜像Chern数。对于拓扑材料,为了给出正确的拓扑不变量和贝里曲率,得到正确的参数符号甚至更为重要。
总之,这篇论文认为从wannier90得到hopping参数的方法更好。
参考文献
[1] Y. Wang, C. Huang, D. Li, P. Li, J. Yu, Y. Zhang, J. Xu, Tight-binding model for electronic structure of hexagonal boron phosphide monolayer and bilayer, J Phys Condens Matter, 31 (2019) 285501.
[2] S. Fang, R. Kuate Defo, S.N. Shirodkar, S. Lieu, G.A. Tritsaris, E. Kaxiras, Ab initio tight-binding Hamiltonian for transition metal dichalcogenides, Physical Review B, 92 (2015).
六、李正中书中紧束缚方法




还有阎守胜固体物理书。
七、sun kai 讲义中紧束缚方法等(实空间紧束缚法)
【金山文档】 sunkai 第五章 紧束缚 笔记
https://kdocs.cn/l/ciefyHsKT2yy
一些微信公众号和博客中的紧束缚模型
- https://mp.weixin.qq.com/mp/appmsgalbum?__biz=MzI3MzIyMjI2Nw==&action=getalbum&album_id=2360622214565380096&scene=173&from_msgid=2247489582&from_itemidx=1&count=3&nolastread=1#wechat_redirect
- https://mp.weixin.qq.com/s/80_dBeUypoXwXJ-kkUTB-g
- https://www.guanjihuan.com/archives/410
- https://yxli8023.github.io/archive.html
本文由"初心如磐,使命在肩!"编辑,转载或引用需注明来源。

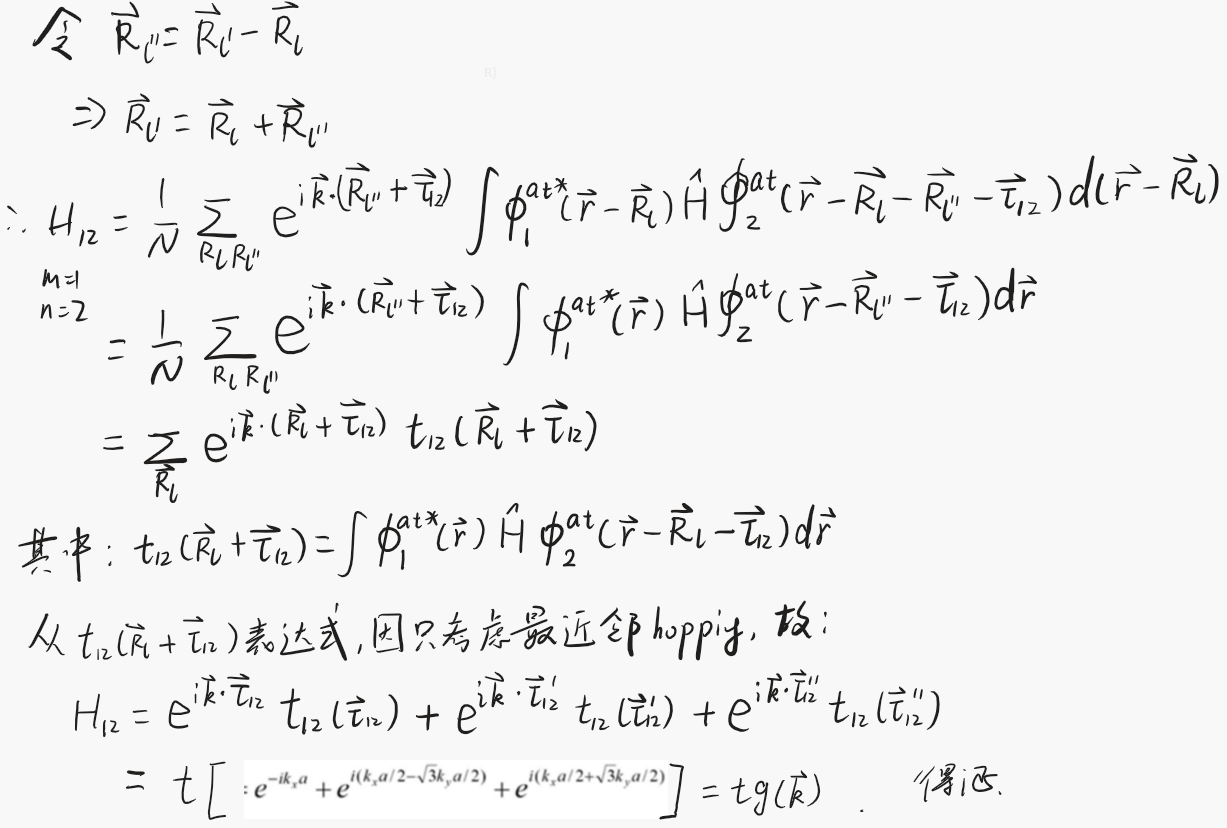



【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 10年+ .NET Coder 心语 ── 封装的思维:从隐藏、稳定开始理解其本质意义
· 地球OL攻略 —— 某应届生求职总结
· 提示词工程——AI应用必不可少的技术
· Open-Sora 2.0 重磅开源!
· 周边上新:园子的第一款马克杯温暖上架