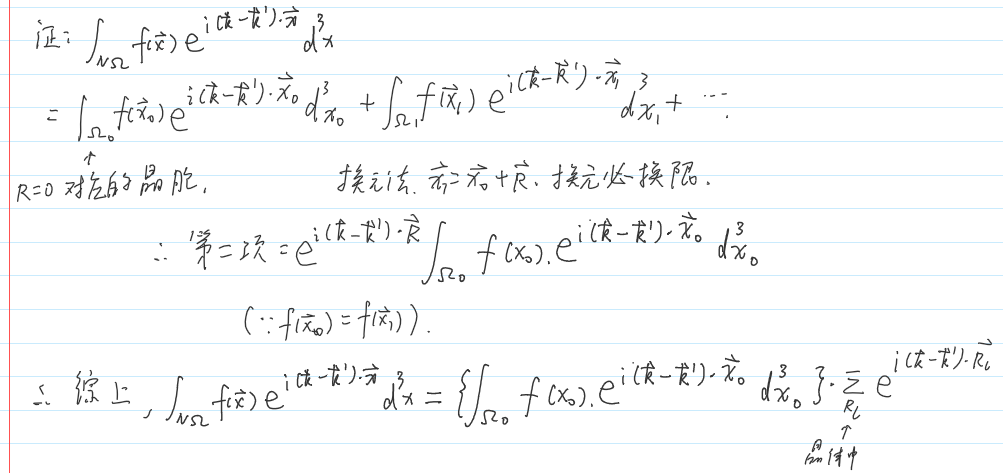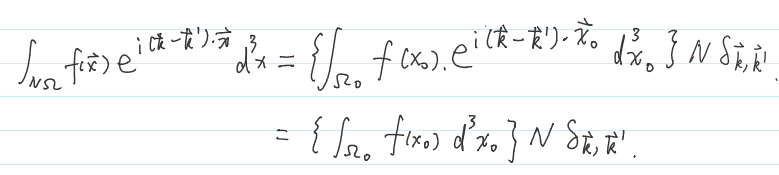傅里叶级数、变换相关的一些结论及其在凝聚态物理中的应用

重要结论

重要结论1：周期函数乘e指数的积分 (此结论在很多公式推导中都可以使用）

当\(\pmb{k}、\pmb{k'}\)都限制在第一布里渊区，且\(f(\mathbf{x})\)是一个正空间周期函数时，有：

\[\begin{equation} \int_{N \Omega} f(\vec{x}) e^{i\left(\vec{k}-\vec{k}^{\prime}\right) \cdot \vec{x}} d^{3} x=\left\{\int_{\Omega_{0}} f\left(x_{0}\right) d^{3} x_{0}\right\} N \delta_{\vec{k}, \vec{k}^{\prime}} \end{equation} \]

其中\(\Omega_0\)是\(R=0\)对应的晶胞，\(x_0\)限制在\(\Omega_0\)中。

以上是在k离散的情况下的公式，在k连续情况下，此式虽然也成立，但还可以写成delta函数的形式，原因：

上式证明过程中用了李正中书（1.3.16）：

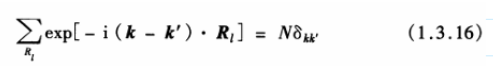
（(1.3.16)是在k是离散的情况下的公式。若在k连续的情况下，则因为\(\Delta k=\frac{(2\pi)^3}{N\Omega}\),此式N很大，故可以认为：

\[\sum_{R_{l}} \exp \left[-\mathrm{i}\left(\boldsymbol{k}-\boldsymbol{k}^{\prime}\right) \cdot \boldsymbol{R}_{l}\right]=\delta(\mathbf{k}-\mathbf{k}^{\prime}) \]

）

证明：

（注意，相差一个倒格矢也会等于1！）

故得证：

---

重要结论2：布洛赫波、布洛赫波的振幅的正交性、完备性

从callaway英文书29和30页知，对布洛赫波：k连续时，

\[\begin{equation} \begin{array}{l} \int_{全空间} \psi_{n}^{*}(\vec{k}, \vec{r}) \psi_{l}(\vec{q}, \vec{l}) d^{3} r=\delta_{n l} \delta({\vec{k}- \vec{q}} )\text {. }\\ \sum_{n} \int_{B Z} \psi_{n}^{*}(\vec{k}, \vec{r}) \psi_{n}\left(\vec{k}, \vec{r}^{\prime}\right) d^{3} k=\delta\left(\vec{r}-\vec{r}^{\prime}\right)\\ \end{array} \end{equation} \]

全空间指的是\(N\Omega\)，N为晶胞数

（2）在callay英文书28和39页有证明。

k看成连续和k看成离散情况时的布洛赫波的表达式见callaway英文书28和29页：

k连续时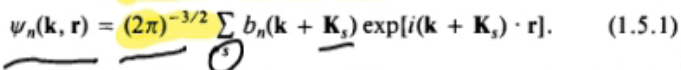：，正交归一性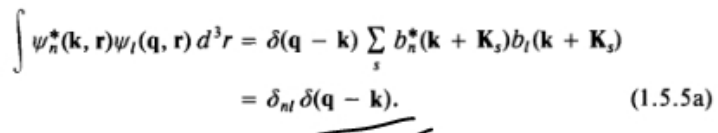：，完备性略；

k离散时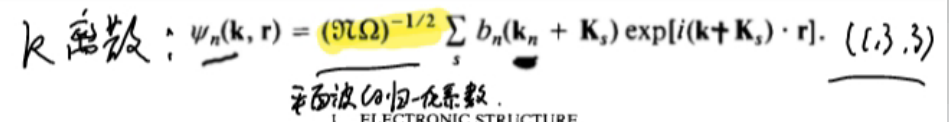：，正交归一性：，完备性略；

设k连续时的布洛赫波函数为\(\psi_{n \vec{k}}(\vec{x})\)，k离散时的布洛赫波函数为\(\psi^{\prime}_{n \vec{k}}(\vec{x})\), 则（1.5.5b）实际上应写为：

\[\int_{全空间} \psi_{n}^{\prime*}(\vec{k}, \vec{r}) \psi_{l}^{\prime}(\vec{q}, \vec{l}) d^{3} r=\delta_{n l} \delta_{\vec{k}, \vec{q}}\tag{1.5.5b} \]

k离散时的布洛赫波函数和k连续时的布洛赫波函数的关系：

\[\psi^{\prime}_{n \vec{k}}(\vec{x})=\frac{{(2\pi)}^{3/2}}{(N\Omega)^{1/2}}\psi_{n \vec{k}}(\vec{x})\tag{*} \]

k离散时，

\[\begin{equation} \begin{array}{l} \int_{全空间} \psi_{n}^{\prime*}(\vec{k}, \vec{r}) \psi^{\prime}_{l}(\vec{q}, \vec{l}) d^{3} r=\delta_{n l} \delta_{\vec{k}, \vec{q}} \\ \sum_{n}\sum_{k}^{BZ} \psi_{n}^{\prime*}(\vec{k}, \vec{r}) \psi^{\prime}_{n}\left(\vec{k}, \vec{r}^{\prime}\right) d^{3} k=\delta\left(\vec{r}-\vec{r}^{\prime}\right)\\ \text { if } \vec{k}=\vec{q}, 则 \int_{全} \psi_{n}^{\prime*}(\vec{k}, \vec{r}) \psi^{\prime}_{l}(\vec{k}, \vec{r}) d^{3} r=\delta_{n l} \text {. } \end{array} \end{equation} \]

(3)中的第二个公式，即k离散时的布洛赫波的完备性公式可以从（*）式、(2)以及\(\sum_{k}=\sum_{k} \frac{\Delta k}{\Delta k}=\sum_{k} \frac{\Delta k}{\frac{(2 \pi)^{3}}{N \Omega}}=\frac{N \Omega}{(2 \pi)^{3}} \int d^{3} k\)来证明，我证了。

k离散时，对布洛赫波的振幅，只能从（3）的第一个公式得到：布洛赫波振幅的正交性：

\[\begin{equation} \begin{aligned} &\int_{\text {cell }} u_{n}^{*}(\vec{k}, \vec{r}) u_{l}(\vec{k}, \vec{r}) d^{3} r=\frac{1}{N} \delta_{n l} \text {. }\\ \Leftrightarrow & \int_{N\Omega} u_{n}^{*}(\vec{k}, \vec{r}) u_{l}(\vec{k}, \vec{r}) d^{3} r= \delta_{n l} \text {. } \end{aligned} \end{equation} \]

1.注意在callaway书（1.5.7）并不是这个公式，(1.5.7)是想证明k连续时的对应公式。我这里(4)是k离散时的布洛赫波的振幅的正交性。

2.(4)的证明：

(4)的证明可以利用上面重要结论1:对于正空间周期函数f(x)，有 \(\int_{N \Omega} f(\vec{x}) e^{i\left(\vec{k}-\vec{k}^{\prime}\right) \cdot \vec{x}} d^{3} x=\left\{\int_{\Omega_{0}} f\left(x_{0}\right) d^{3} x_{0}\right\} N \delta_{\vec{k}, \vec{k}^{\prime}}\)来证明：

从(3)的第一个公式：

\[\begin{equation} \int_{N \Omega} \psi_{n k}^{\prime{*}}(\vec{r}) \psi_{l\vec{q}}(\vec{r}) d^{3} r=\delta_{n l} \delta_{\vec{k},\vec{q}} \end{equation} \]

将\(\psi_{n k}^{\prime}=e^{i \vec{k} \cdot \vec{r}} u_{n k}\)代入(5)的左边,得：

\[\begin{equation} \begin{aligned} \text { left hand of (5) } &=\int_{N \Omega} e^{-i \vec{k} \cdot \vec{r}} u_{n k}^{*} e^{i \vec{q} \cdot \vec{r}} u_{l\vec{q}}(\vec{r}) d^{3} r \\ &=\int_{N \Omega} u_{n k}^{*} u_{l \vec{q}} e^{i(\vec{q}-\vec{k}) \cdot \vec{r}} d^{3} r \\ &=\left(\int_{\Omega_{0}} u_{n k}^{*} u_{l q} d^{3} r\right) N \delta_{k, q} \\ &=\left(\int_{N \Omega} u_{n k}^{*} u_{l\vec{q}} d^{3} r\right) \delta_{k, q} \\ &=\left(\int_{N \Omega} u_{n k}^{*} u_{l k} d^{3} r\right) \delta_{k, q} \end{aligned} \end{equation} \]

第二个等号到第三个等号是应用了重要结论1，第三个等号到第四个等号是由于上式中\(u_{n}^{*}(\vec{k}, \vec{r}) u_{l}(\vec{k}, \vec{r})\)是正空间周期函数。

从(5)(6)即知\(\int_{N\Omega} u_{n}^{*}(\vec{k}, \vec{r}) u_{l}(\vec{k}, \vec{r}) d^{3} r= \delta_{n l} \text {. }\)得证。

另外，并不能从布洛赫波的完备性的公式得到一个比较好的只关于布洛赫波的振幅的完备性的公式，所以callaway书也没有提到布洛赫波振幅的完备性的公式。

k连续时布洛赫波振幅的正交性：有吗？不知道，没时间，以后自己再证明

---

重要结论3：周期函数的格林定理：实空间或倒空间的周期函数的梯度在原胞或1BZ中的积分

在A&M的固体物理书的附录I中证明了：对一个在倒空间中具有周期性的函数，对其求梯度，然后再对BZ积分，结果就是0. （此结论来自93年sipe11714页)

证明：对于k空间周期函数，在（1.1）中令u=1，即得证上面结论。

参考文献

[1] callaway.固体量子理论书

[2] 李正中.固体理论书

[3] Ashcroft&Mermin. Solid State Physics书

[4] E. I.Blount, Solid State Physics:AdvancesinResearch and Applications (Academic ,NewYork, 1962), Vol.13