晶体点群、空间群简要归纳

本文只是很简要的归纳，具体内容还请见李新征老师群论书和其在蔻享的群论课。

另外推荐肖瑞春老师科学网博客的这篇博文，介绍了群论及后续的学习：科学网—群论学习资料备忘录(凝聚态物理专业) - 肖瑞春的博文 (sciencenet.cn)
若研究中涉及群论和物理性质相关，其中陈纲的《晶体物理学基础》书特别好，易懂，将主动变换和被动变换等分析得特别清晰，不过此书太厚，注意用到什么学什么，用minimized的知识来科研，否则被导师批评...

1.对称操作、对称元素

对称操作：保持系统不变的操作。

对称元素：它是一个几何实体，对称操作可以依据对称元素施行对称操作。对称元素可以是点、直线、面等。

2.点群：

1）定义：三维实正交群O(3)群的有限子群

物理理解：实际上点群是实际的物理系统在三维空间的一些对称操作的集合。这些对称操作会保持一个点不动。

2）点群分类

第一类点群：只包含纯转动元素的点群。

第二类点群：点群中，除了纯转动元素，还包含转动反演元素的点群。

因为点群是O(3)群的子群，而O(3)群中有固有转动和非固有转动。

3）点群的性质
  • 性质1：点群这个集合可以写成{Ck→(2π/n)、ICk→′(2π/n′)}的形式，其中

n,k→′,n′取有限个方向和值；Ck→(2π/n)是绕k→轴转2π/n角的操作。

  • 性质2：设G是点群，K是G的纯转动部分，由于纯转动部分的乘积以及逆元必属于这个纯转动部分,所以K也是G的纯转动子群,即K=G∩SO(3)∘.

点群G与其有限子群K的关系有以下三种可能的情况：

  • 1.G=K, 即点群只包含纯转动操作；称为第一类点群。
  • 2.若点群G中除了纯转动操作，还包含纯空间反演操作I, 则可以通过G=K∪IK得到这种情况对应的第二类点群。
  • 3.若点群G中除了纯转动操作，且G中不包含纯反演操作I时 , 此第二类点群G一定与一个第一类G+同构,其中，G+=K∪K+, 而K+定义为:K+={Ig∣g∈G, 但 g∉K} 

根据这里的第3点，可以知道构造这种情况对应的第二类点群的方法：根据一个已知的第一类点群K∪K+，即可以构造一个第二类点群K∪IK+.

还可以证明K必须是K∪K+的不变子群，其阶数是K∪K+的一半。所以在构造第二类点群时，关键是找到已知的第一类点群的不变子群K。

3.第一类点群

共5种：

Cn群、Dn群、

T群：12个元素，4个类：

{E},{C2,C2′,C2′′},{C3,C3′,C3′′，C3′′′},{C32,C3′2,C3′′2,C3′′′2}

O群：24个元素，5个类：

{E},{C2(1),C2(2),C2(3),C2(4),C2(5),C2(6)}

{C3,C3′,C3′′,C3′′′,C32,C3′2,C3′′2,C3′′′2},{C4,C4′,C4′′,C43,C4′3,C4′′3}

{C42,C4′2,C4′′2}

Y群：60个元素，5个类：

{E}、

{C2(1),C2(2),⋯,C2(15)}

{C3(1),⋯,C3(10),C3(1)2,⋯,C3(10)2}

{C5(1),⋯,C5(6),C5(1)4,⋯,C5(6)4}

{C5(1)2,⋯,C5(6)2,C5(1)3,⋯,C5(6)3}

4.第二类点群

根据点群的性质2，可以得到性质2中的2.的情况对应的第二类点群，共5种：

Cn∪ICn、Dn∪IDn、T∪IT、O∪IO、Y∪IY

根据点群的性质2，可以得到性质2中的3.的情况对应的第二类点群，共4种：

a.将已知的第一类子群K∪K+取为C2n，则不变子群K为：{C2n2,C2n4,⋯,C2n2n=E}，陪集K+为：{C2n,C2n3,…,C2n2n−1}，故构造一个第二类点群K∪IK+为：{{C2n2,C2n4,⋯,C2n2n=E},I{C2n,C2n3,⋯,C2n2n−1}}

b.将已知的第一类子群K∪K+取为Dn，不变子群取为Cn，故第二类子群：{{Cn,Cn2,⋯,E},I{C2(1),C2(2),⋯,C2(n)}}

c.将已知的第一类子群K∪K+取为D2n，不变子群取为Dn，故第二类子群：

{{C2n2,C2n4,⋯,C2n2n=E,C2(2),C2(4),⋯,C2(2n)}，I{C2n,C2n3,⋯,C2n2n−1,C2(1),C2(3),⋯,C2(2n−1)}}

d.将已知的第一类子群K∪K+取为O，不变子群取为T，故第二类子群：{{C3,C3′,C3′′,C3′′′,C32,C3′2,C3′′2,C3′′′2,E1C42,C4′2,C4′′2}，I{C2(1),C2(2),C2(3),C2(4),C2(5),C2(6),C4,C4′,C4′′,C43,C4′3,C4′′3}}

以上就是所有可能的点群。

5.schoenfiles符号

见书117页.

根据书知道：

用schoenfiles符号来表示第二类点群，则形式上有9种情况（实际上有13种）。

若再加上第一类点群的5种，则用schoenfiles符号来表示点群一共有14种情况：

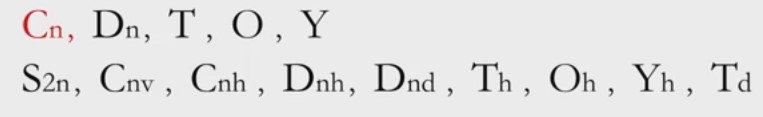
这14种情况对应的对称操作见李新征书从106页至120页的内容！！！
以后在科研中遇到一个schoenfiles符号，我就先找李书117页图3.17，再根据106页至120页的内容找出其对称操作。

schoenfiles符号见116页

另外，这14种情况对应的实际例子有：（书中没有写）

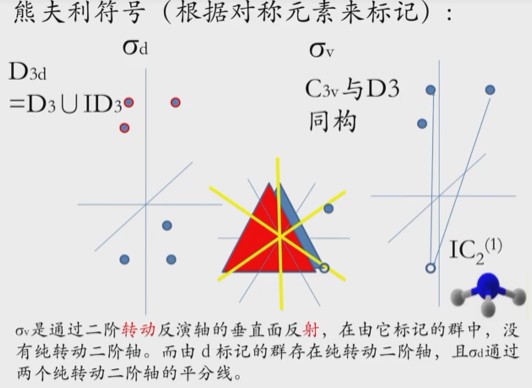
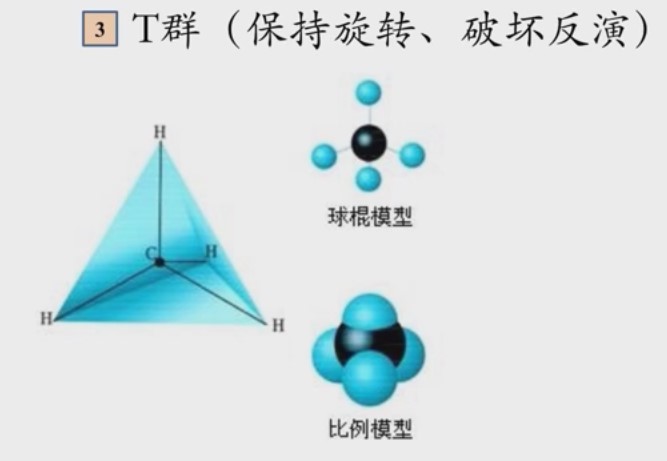
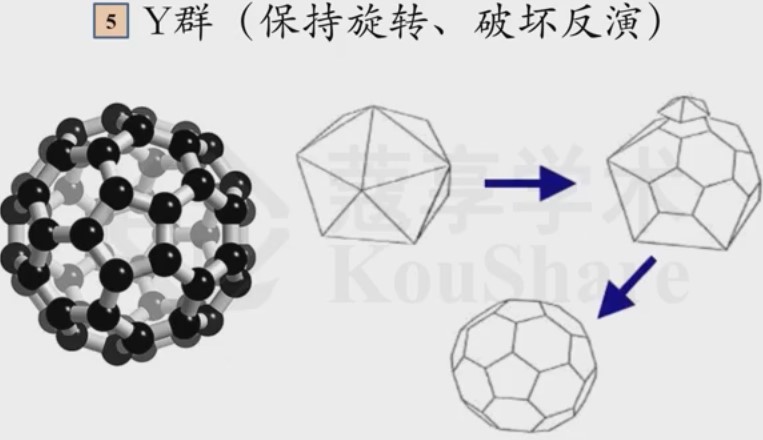
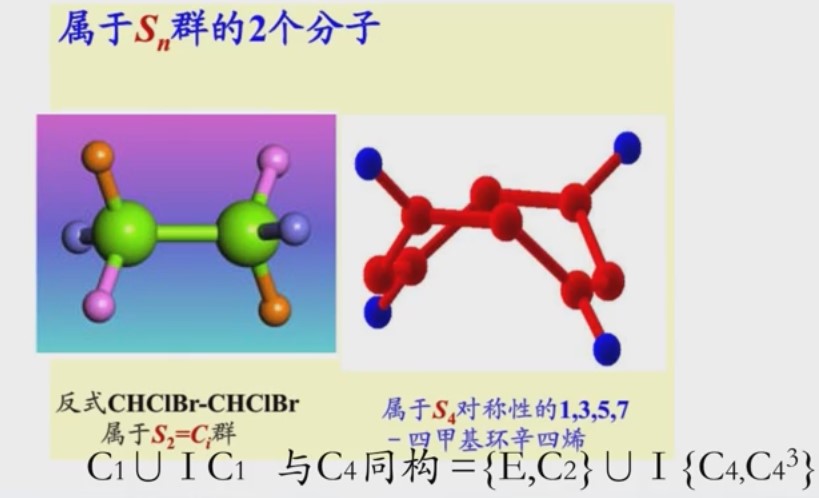
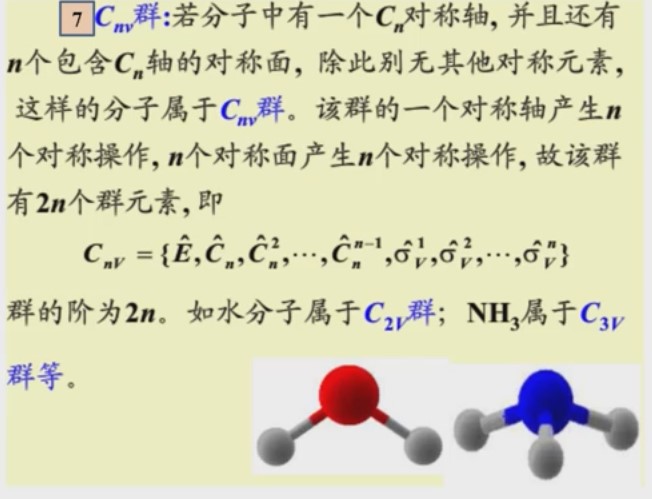
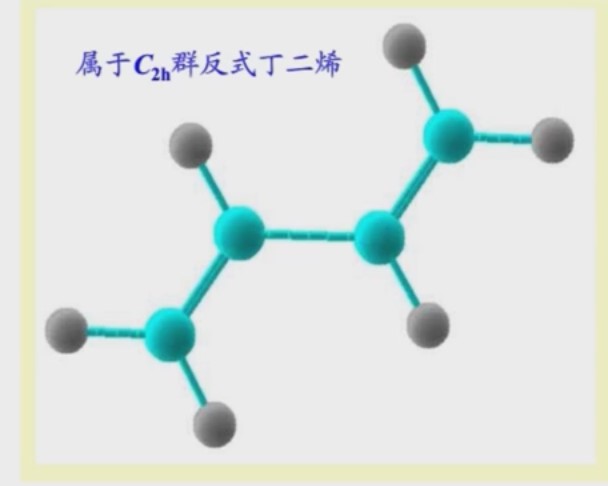
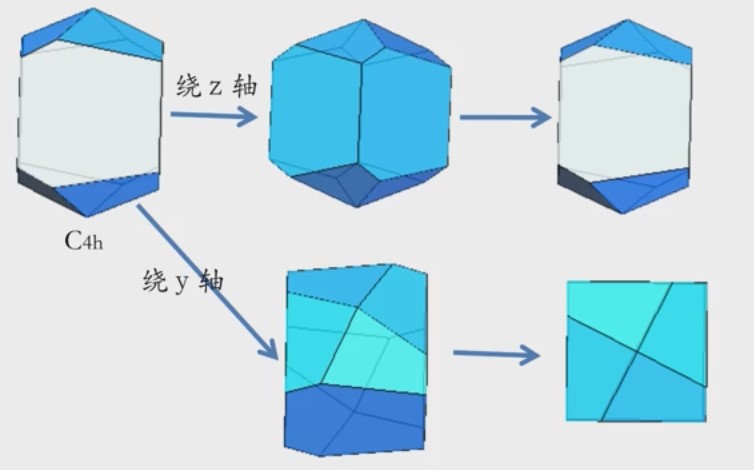
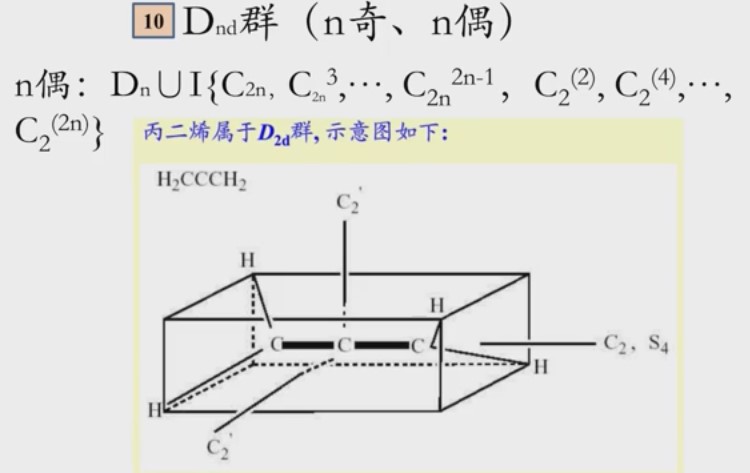
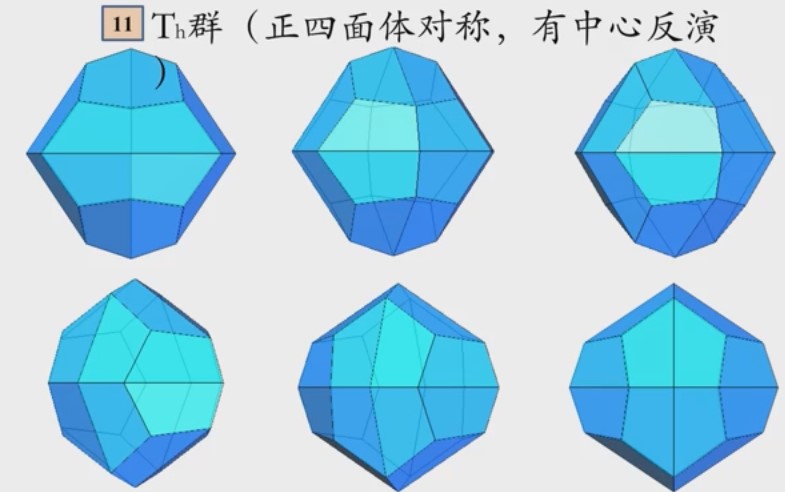
Oh是晶体中最高的对称性，再往后的对称性更高的点群形成不了晶体。

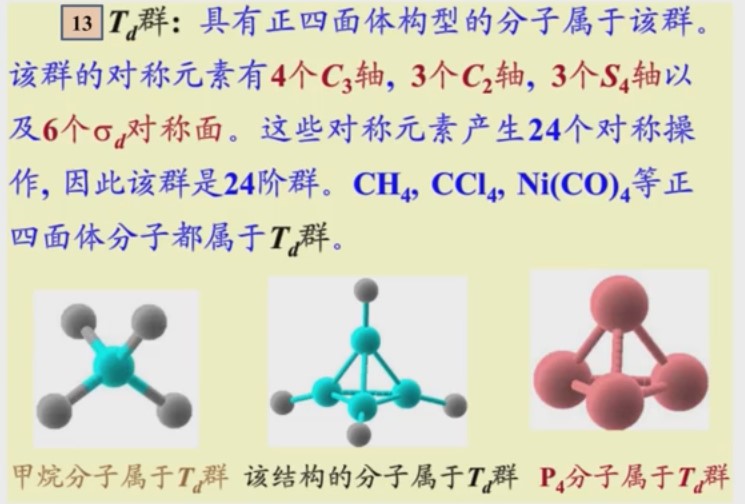
脚标d的含义见118页

6.晶体点群

  • 晶体：有转动（包括转动反演）、平移对称性
  • 晶体点群：不考虑平移对称性，只考虑转动对称性，即晶体点群是能够将晶体变到其本身的转动、转动反演操作的集合。
  • 晶体制约定理：设G是晶体点群，则G中的转动元素只能由E,C2,C3,C4，C6生成,G中的转动反演元素只能早IE,IC2,IC3,IC4,IC6生成. 其中C2是绕二阶轴的转动。
  • 根据晶体制约定理，可以知道，可以在晶体中出现的点群只有：

a.第一类点群中可以在晶体中出现的只有：C1,C2,C3,C4,C6,D2,D3,D4,D6,T,O

b.第二类点群可以在晶体中出现的只有：

S2,S4,S6，C2v,C3v,C4v,C6v,C1h,C2h,C3h,C4h,C6h,D2d,D3d,Th,Td,Oh

以上就是可能存在的32种晶体点群。

7.晶系

  • 定义：将32种晶体点群按照是否有共同的对称操作的对称元素来划分，而具有相同的对称元素会使得晶体在宏观对称性上会有一些相似性，故将这些晶体点群称为一种晶系。

例如T、O、Td,Th,Oh这五种点群都有 4 个三阶轴这个对称元素，这就导致从宏观上看晶体，x，y，z轴都等价，故将它们划分为一种晶系，称为立方晶系。

  • 晶胞：能反映晶体对称性的最小结构单元。晶系中相同的对称元素的共同特征可以由晶胞参数(a→,b→,c→、α、β、γ）反映出来。

8.布拉维格子（晶格）

  • 对一个属于某个晶系的点群，例如Oh群，若只是由a→,b→,c→形成的一个晶胞的顶点有原子，则可以形成一种晶体，但是如果在此晶胞的体心加一个原子，则形成另一种晶体，它也具有Oh点群对称性。这两种晶体不一样，但是点群和晶系两个概念不能描述这种差别，故引入布拉维格子（晶格）的概念。一共14种。
  • 晶格是一个空间群概念。
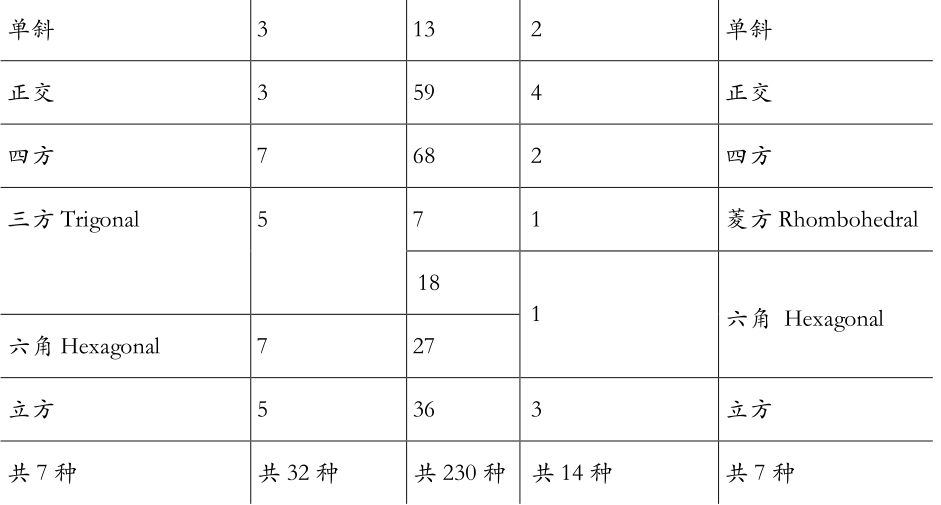
  • 晶格系统：7种。每种容纳几个布拉维格子，一共容纳14种。
  • 晶格系统与晶系的差别：

晶系是基于晶体点群对称性对晶体的分类。

晶格系统是基于晶体的空间群对称性对晶体的分类。

晶系与晶格系统见此表：

  • 7种晶格系统，在晶胞上分别增加体心、面心等原子，要求这种增加不改变晶胞的点群对称性且增加后，晶胞不能被进一步简化为更小的可反映点群对称性的晶胞。这样就得到了所有的14种布拉维格子。

9.Hermann-Mauguin符号（即国际符号）

用不等价的轴或平面来标记晶体的对称性。具体见书129页，有32种点群在国际符号下的表示：130页。

  • 需要用到空间群时，先看其国际符号（Hermann-Mauguin符号），然后有相关网站可以查出此群对应的所有对称操作。通过这些对称操作得到晶体结构的方法见书138页。最后就得到了晶体结构。

10.空间群

  • 定义：既考虑晶体的转动不变性，又考虑平移不变性，这些对称操作的集合。
  • 对称操作：{R∣t→}，其中R：转动操作；t→：平移操作。
  • 简单空间群：将晶系中布拉维格子的平移操作的种类与晶系种晶体点群的种类进行组合，得到的就是此晶系中简单空间群的种类。所有的简单空间群一共73种。

例如对立方晶系，有简单、 体心、 面心三种格子，T、 O、Th、Td、Oh五种点群，组合得到3X5=15种简单空间群。

  • 非简单空间群：{R∣t→}中的t→并不是空间平移对称性最小重复单元的整数倍，而是其分数倍，例如螺旋轴和滑移面两种情况中就会存在以上所说的分数倍的对称操作。

非简单空间群有157种。

  • 空间群一共230种。

11.晶体点群的不可约表示（重要）

参考文献

[1] 李新征.群论及其在凝聚态物理中的应用.

[2] 蔻享的李新征群论课

posted @   初心如磐使命在肩！  阅读(6755)  评论(0)  编辑  收藏  举报
编辑推荐：
· 10年+ .NET Coder 心语，封装的思维：从隐藏、稳定开始理解其本质意义
· .NET Core 中如何实现缓存的预热？
· 从 HTTP 原因短语缺失研究 HTTP/2 和 HTTP/3 的设计差异
· AI与.NET技术实操系列：向量存储与相似性搜索在 .NET 中的实现
· 基于Microsoft.Extensions.AI核心库实现RAG应用
阅读排行：
· 10年+ .NET Coder 心语 ── 封装的思维：从隐藏、稳定开始理解其本质意义
· 地球OL攻略 —— 某应届生求职总结
· 提示词工程——AI应用必不可少的技术
· Open-Sora 2.0 重磅开源！
· 周边上新：园子的第一款马克杯温暖上架
点击右上角即可分享
微信分享提示
AI IDE Trae