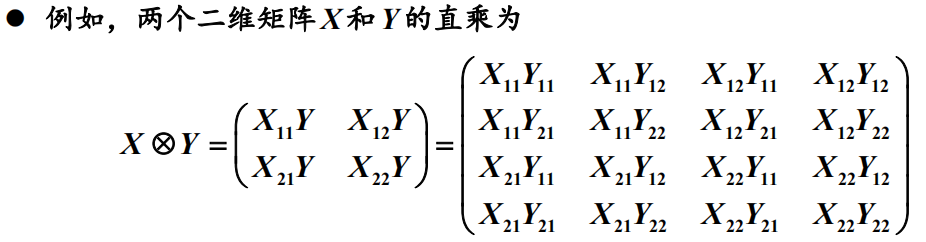物理学中的群论第一章线性代数

声明：这是我根据黄飞老师上课内容记的笔记（易懂）。教材：马中骐的物理学中的群论书（不好懂，所以我没看）。希望对学群论的人有所帮助。

物理学中的群论第一章线性代数
声明：这是我根据老师上课内容记的笔记（易懂）。教材：马中骐的物理学中的群论书（不好懂，所以我没看）。希望对学群论的学生有所帮助。
1.1节线性空间和矢量基
1.矢量基
2.矢量
3.m维线性空间：就是定义了加法和数乘
4.实线性空间：
5.矢量、基矢量的矩阵表示
6.线性空间的维数
1）线性相关、线性无关
2）线性空间的维数
7.线性空间的子空间
8.两个子空间的和
9.两个子空间的交
10.两个子空间的直和
11.线性空间举例
1）m维函数空间
2）矢量、函数基
1.2节线性变换和线性算符
1.矩阵
2.矩阵乘法、逆矩阵、非奇异矩阵
3.向量组线性无关与矩阵的秩的关系
4.共轭矩阵：先转置再取复共轭（重要）
5.矩阵与对角矩阵对易的结论：
6.线性变换
7.对算符 R(x)不变的空间（简并子空间）
简并子空间：
简并子空间的性质（重要，背这句话）：
对算符 R(x)不变的空间：
基矢的变换、算符R(x)的矩阵形式
态矢的变换的矩阵形式
8.关于算符R的不变空间的一般定义
基矢的变换的矩阵形式：
态矢的变换的矩阵形式
9.线性空间

L

中关于R的不变子空间

L_{1}

1.3节相似变换
1.基矢的变换
2.变换算符在原矢量基的矩阵表示：
3.态矢的变换
4.算符的变换：
5.相似变换
相似变换的基本关系式：
1.4节本征矢量和矩阵对角化
本征方程的矩阵表示
算符在自身表象的表示：对角线是本征值
久期方程
久期方程m个根的和与积：
能够相似变换对角化的充要条件及如何进行相似变换对角化：
联系两个所有本征值都相同的非对角矩阵A、B间的相似变换矩阵的方法：
1.5节矢量内积
1.线性空间两矢量的内积

⟨ a | b ⟩

2.由矢量基

e_{µ}

的内积构造矩阵

Ω

：
3.任意两矢量的内积：
4.归一化矢量、矢量正交、非零正交矢量线性无关
5.算符的矩阵形式
6.共轭算符
1.6节幺正矩阵、厄米矩阵、正交矩阵、实对称矩阵
1.幺正矩阵
2.厄米矩阵
3.正交矩阵和实正交矩阵
4.实对称矩阵
1.7节矩阵的直乘
直乘的性质
1）直乘矩阵的维数等于因子矩阵维数的乘积。
2）直乘矩阵的迹：
3）设矩阵X1和X2维数相同, 矩阵Y1和Y2维数相同，则：
3）直积后的行列式
4）直积后的导数
5）直积没有交换律

TOC

这两章线性代数考试不会考，但非常重要，后面都在用。

1.1节线性空间和矢量基

1.矢量基

有加法和数乘、一组线性无关的客体

2.矢量

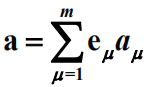
3.m维线性空间：就是定义了加法和数乘

m个基矢量对应m维
简单来说，线性空间就是矢量空间，线性空间中只有加法和数乘（即只有两个矢量相加、数乘），但是没有矢量乘法，也没有长度这样的概念。
如果在线性空间中引入点乘，长度、垂直的概念，此时称为内积空间。

线性空间性质：

4.实线性空间：

5.矢量、基矢量的矩阵表示

矢量矩阵表示：列矩阵

基矢量矩阵表示：
$e_{μ}$ 按基矢量 $e_{1} 、 e_{2} 、 e_{3} . . .$ 展开，其第 $ν$ 个分量为

基矢量矩阵表示是只有一个分量为1，其他分量为零的列矩阵。

6.线性空间的维数

1）线性相关、线性无关

2）线性空间的维数

线性空间的维数：线性空间中线性无关的矢量的最大个数。

m维线性空间中，线性无关的矢量数目不能大于m。

矢量基是线性无关的，m 维线性空间中任何 m 个线性无关的矢量都可以作为一组矢量基。

7.线性空间的子空间

子空间就是在m维线性空间中，有比m维数小的个数的线性无关矢量的所有的线性组合，构成一个n维线性空间。

比如三维空间中，两个基矢量 $e_{x} 、 e_{y}$ 的所有线性组合构成x-y平面，是二维线性空间，是子空间。

我们通常说的子空间是非平庸的子空间，不包括零空间和全空间。

8.两个子空间的和

两个子空间的和：两个子空间 $L_{1}$ 和 $L_{2}$ 的所有矢量及这些矢量的线性组合的集合，记作 $L_{1} + L_{2}$ ；

注意 $L_{1} + L_{2}$ 并非 $L_{1}$ 和 $L_{2}$ 的所有矢量的集合，因为除了将这些矢量放在一块以外，还需要将它们线性组合。例如， $e_{x} 、 e_{y}$ 构成的子空间和 $e_{x} 、 e_{z}$ 构成的子空间的和是整个三维空间。

9.两个子空间的交

两个子空间的交：，

例如， $e_{x} 、 e_{y}$ 构成的二维子空间和 $e_{z}$ 构成的一维子空间的交是零空间（零矢量构成的空间）。

10.两个子空间的直和

两个子空间的直和：若 $L$ 是 $L_{1}$ 、 $L_{2}$ 的和（即），且下面三个等价的条件中任意一条成立：

则 $L$ 称为两个子空间 $L_{1}$ 和 $L_{2}$ 的直和，记作 $L = L_{1} \oplus L_{2}$ ，此时 $L_{1}$ 与 $L_{2}$ 称为 $L$ 中互补的子空间。

1.与 $L_{1}$ 相补的子空间并不唯一。
2.例如，三维空间可以看成是 $e_{x} 、 e_{y}$ 构成的二维子空间与 $e_{z}$ 构成的一维子空间的和，也可以说成是这个二维子空间和一维子空间的直和，此时这两个子空间满足上述所说的三个条件。也存在是和而不是直和的情况，如两个二维子空间不可能通过直和组成三维空间。

一个线性空间可以分解为若干个子空间的直和，分解方式并不唯一。

例如，三维空间可以看成是 $e_{x} 、 e_{y}$ 构成的二维子空间与任意一个不在x-y平面内的斜着的任何一个矢量构成的一维子空间的直和。这种分解不唯一。

11.线性空间举例

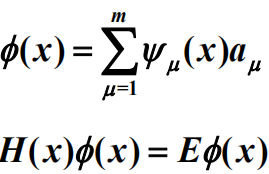
反之，H(x)的本征值为E的本征函数总可以表示成的线性组合。

1）m维函数空间

2）矢量、函数基

1.2节线性变换和线性算符

1.矩阵

行列式：

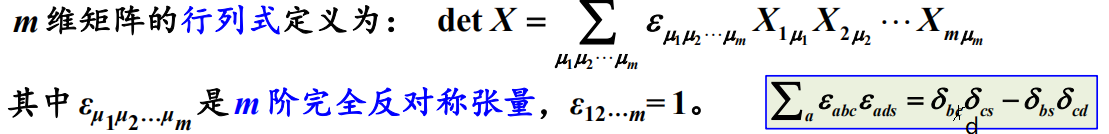
$\sum_{a} ε_{a b c} ε_{a d s} = δ_{b d} δ_{c s} - δ_{b s} δ_{c d}$

2.矩阵乘法、逆矩阵、非奇异矩阵

矩阵乘法：

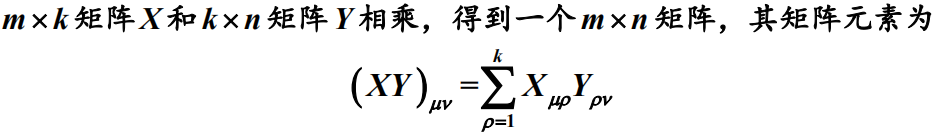
逆矩阵：若两方矩阵相乘为单位矩阵，则这两矩阵互称逆矩阵；
方矩阵存在逆矩阵的充要条件：其行列式不为零。
非奇异矩阵：行列式不为零的方矩阵。

奇异矩阵：行列式为零的方矩阵。

m维空间的任一组矢量基，作为列矩阵排列成的m维方矩阵必是非奇矩阵。

矢量基是只有一个分量为1，其他分量为零。应该可以证明上面的结论。

3.向量组线性无关与矩阵的秩的关系

如果把 m 维空间的 n 个矢量作为列矩阵排列成一个 m x n 矩阵，则此 n 个矢量线性无关的充要条件是此矩阵的秩为n。

此定理的证明：
慕课中，n维向量第三讲中

推论1的证明：此时，由于r(A)小于等于min{m,n}=n，而n<m，故r(A)<m，故由定理4知，线性相关。
推论2的证明：推论2就是直接由推论1和定理4得到，由于一个向量组不是线性相关就是线性无关，又由推论1得：要使得线性无关，必须m小于等于n，而由于r(A)小于等于min{m,n}=m，故r(A)小于等于m，而由定理4知，当r(A)小于m时，线性相关；故要使得线性无关，只有要求r(A)=m，得证。

4.共轭矩阵：先转置再取复共轭（重要）

矩阵行列交换得到的矩阵称为转置矩阵；矩阵元素取复共轭得到的矩阵称为复共轭矩阵；
矩阵元素取转置和复共轭得到的矩阵称为共轭矩阵。

5.矩阵与对角矩阵对易的结论：

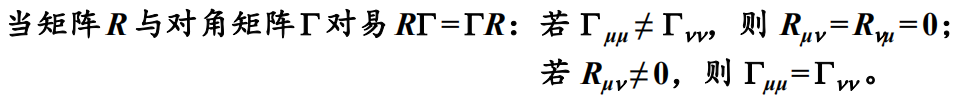
6.线性变换

变换就是给出一种规则，每个函数都能按此规则变成一个确定的函数。
算符是描写变换的一种数学符号。

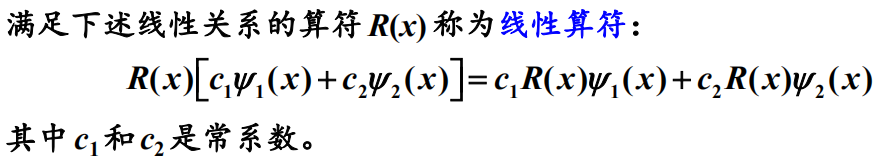
线性变换：线性算符描写的变换

7.对算符 R(x)不变的空间（简并子空间）

简并子空间：

设H(x)的本征值E是m重简并的，它的本征函数 $ψ_{μ}$ （这些 $ψ_{μ}$ 作为基函数）架设一个m维函数空间 $L$ (即简并子空间），这些基函数 $ψ_{μ}$ 的线性组合仍然是对应于同一E的本征函数，即该空间中的任意矢量都是H(x)的本征值为E的本征矢量。

简并子空间的性质（重要，背这句话）：

与 H(x)对易的算符R(x)作用在该空间的任意函数仍是该空间的一个函数，可以表示成函数基的线性组合。

比如，

对算符 R(x)不变的空间：

有以上性质的线性空间 $L$

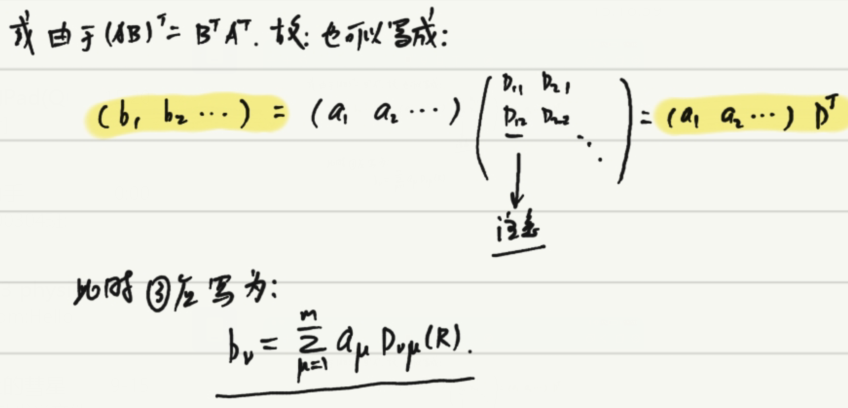
基矢的变换、算符R(x)的矩阵形式

由于一个基函数 $ψ_{μ}$ 对应一个上面的方程，故基矢的变换的矩阵形式：

矩阵D是算符R(x)在空间L中关于这些基函数{ $ψ_{μ}$ }的矩阵形式。

态矢的变换的矩阵形式

态矢的变换的矩阵形式：

8.关于算符R的不变空间的一般定义

基矢的变换的矩阵形式：

，...

态矢的变换的矩阵形式

因为
（1）、
（2）
故由（1）、（2）得：

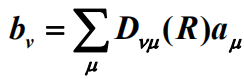
故态矢的变换的矩阵形式：

9.线性空间 $L$ 中关于R的不变子空间 $L_{1}$

其定义：子空间 $L_{1}$ 中的任意矢量，经R作用后仍是该子空间的一个矢量，则称 $L_{1}$ 为线性空间 $L$ 中关于R的不变子空间 $L_{1}$ 。
零空间和全空间是两个平庸的不变子空间。

1.3节相似变换

表象变换：重新选取基后的变换

1.基矢的变换

新基矢：

基矢的变换：

通过“什么东西对行指标求和”就能写出矩阵形式：

逆变换：

矩阵形式：

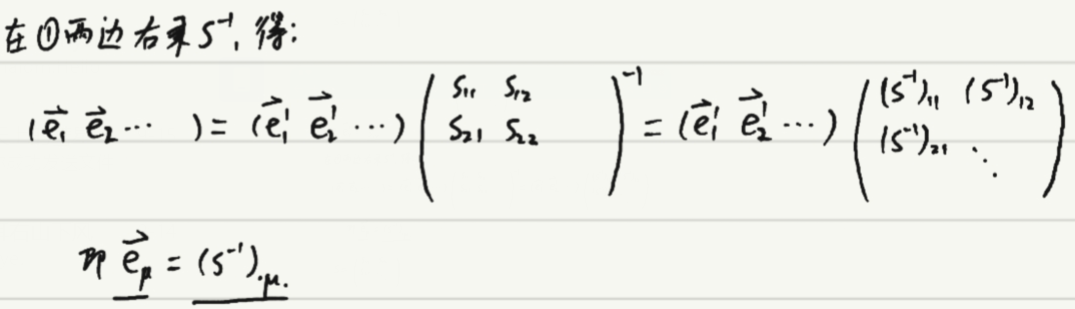
2.变换算符在原矢量基的矩阵表示：

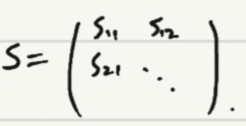
3.态矢的变换

因为
、
故态矢的变换：

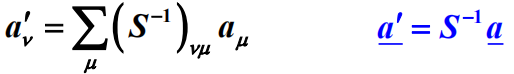
4.算符的变换：

在中代入
、得
（1）；又因为简并子空间的性质“与 H(x)对易的算符R(x)作用在该空间的任意函数仍是该空间的一个函数，可以表示成函数基的线性组合”，故先将在新基展开成线性组合，，再代入，得
（2）
由（1）、（2）得：

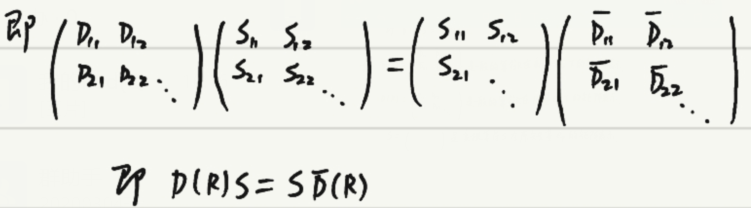
即
重要：

5.相似变换

相似变换：一般的算符R在两表象中的矩阵表示之间的联系称为相似变换。

相似变换的基本关系式：

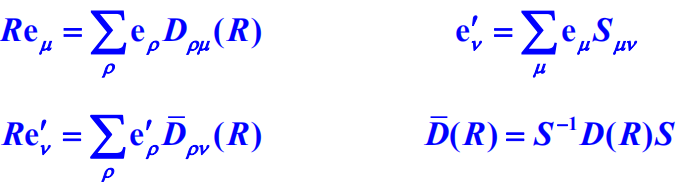
还有以下两个公式成立：
（1）
（2）【此公式错误】

1.(1)的证明见前面基矢的变换。
2.我认为（2）是错误的，因为：
。
3.我认为只有以下公式：
由简并子空间的性质“与 H(x)对易的算符R(x)作用在该空间的任意函数仍是该空间的一个函数，可以表示成函数基的线性组合”，得：
类似1.2节6.中基矢的变换，有：

1.4节本征矢量和矩阵对角化

R作用于矢量a上，得到的 $λ a$ 依然在a构成的一维子空间中，由不变子空间的定义知，是不变子空间。

本征方程的矩阵表示

在关于R的一个m维不变空间 $L$ 中，任意选定矢量基 $e_{µ}$ 后，由本征方程得到：

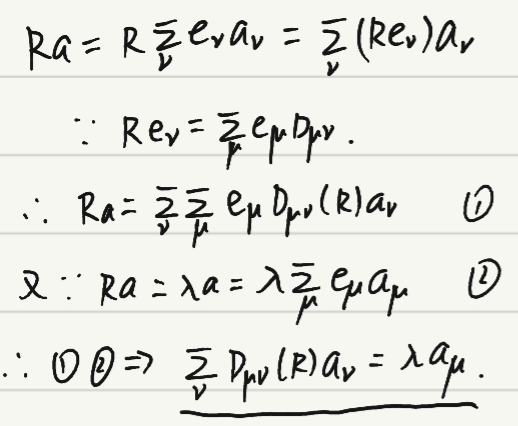
本征方程的矩阵表示：

和华中师范书表象变换一样

算符在自身表象的表示：对角线是本征值

若能在此关于R的不变空间 $L$ 中找到R的m个线性无关的本征矢量作为新基（这些新基分别对应R的本征值 $λ_{μ}$ ，则R在此新基中的矩阵表示为对角矩阵，对角元就是本征值。

基矢的变换：

通过相似变换将D(R)对角化，关键是找R的m个线性无关的本征矢量。

如何进行相似变换对角化（非常重要）见秦静线性代数书125至128页

久期方程

由本征方程的矩阵形式知，本征方程是关于 m 个变量 $a_{µ}$ 的联立线性方程，有非零解的充要条件是变量的系数行列式为零——久期方程：

久期方程在相似变换中保持不变，本征值与矢量基的选择无关。

证明：因为

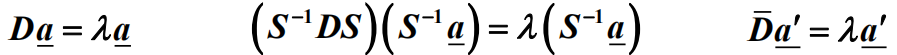
久期方程m个根的和与积：

由久期方程知，久期方程是关于本征值的m次代数方程，有m个根，这m个本征值的和与积分别为：

线性代数可以证，没时间

能够相似变换对角化的充要条件及如何进行相似变换对角化：

充要条件：久期方程无重根或有重根但对每个重根有与重数相同的线性无关的本征矢，则由所有线性无关的本征矢易得相似变换矩阵 S。若有重根，但得不到与重数相同的线性无关的本征矢，则D(R)不能通过相似变换对角化。
以上结论的证明及如何进行相似变换对角化（非常重要）见秦静线性代数书125至128页，特别是定理4.2.1

联系两个所有本征值都相同的非对角矩阵A、B间的相似变换矩阵的方法：

在可以通过相似变换对角化的情况下，求联系两个所有本征值都相同的非对角矩阵A、B间的相似变换矩阵的方法：
1）将A、B的相似变换为对角阵，注意所有本征值相同

2）由得
即联系这两个所有本征值都相同的非对角矩阵的相似变换矩阵为

1.5节矢量内积

1.线性空间两矢量的内积 $⟨ a | b ⟩$

2.由矢量基 $e_{µ}$ 的内积构造矩阵 $Ω$ ：

其分量：
由矢量基的内积构造的矩阵是特征值都大于零的厄米矩阵

是厄米矩阵的证明：

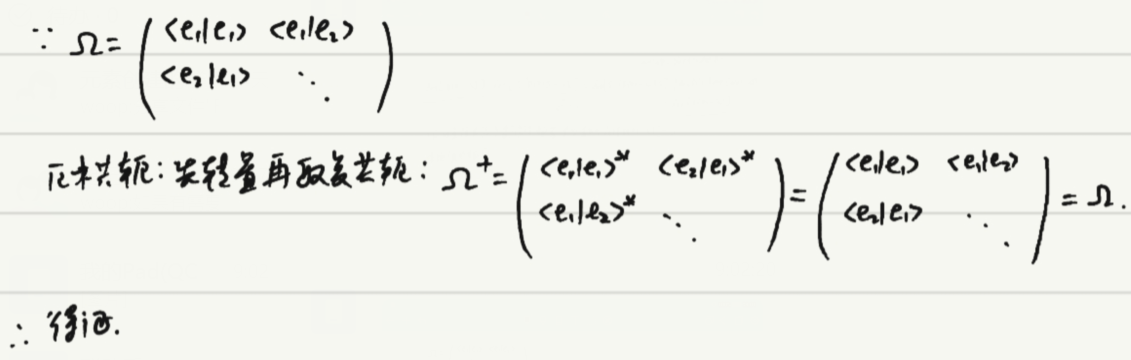
是正定矩阵（？）的证明：
这里所说的正定是广义的正定（？但广义的正定要求对任意向量都成立而不是本征矢量）：

狭义的正定是对实对称矩阵来说的，实对称矩阵：如果有n阶矩阵A，其矩阵的元素都为实数，且矩阵A的转置等于其本身（aij=aji），(i,j为元素的脚标），则称A为实对称矩阵。但 $Ω$ 不是实对称矩阵。
不知道能否由广义正定矩阵定义来证明它是广义正定矩阵。没时间，算了

证明特征值都大于零：

得证。

3.任意两矢量的内积：

故：

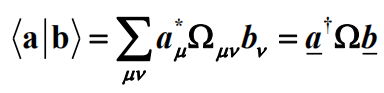
注意，这个结果并不是一般的，这是因为这个结果是矢量基不正交归一化时的普遍表达式。当矢量基不正交归一时，矢量内积和列矩阵内积并不相同。

4.归一化矢量、矢量正交、非零正交矢量线性无关

1）模为1的矢量称为归一化矢量；
2）若两矢量内积为零，称为两矢量正交;
3）非零正交矢量线性无关。

5.算符的矩阵形式

未选择正交归一矢量基时，矢量基取定后，算符的矩阵形式：

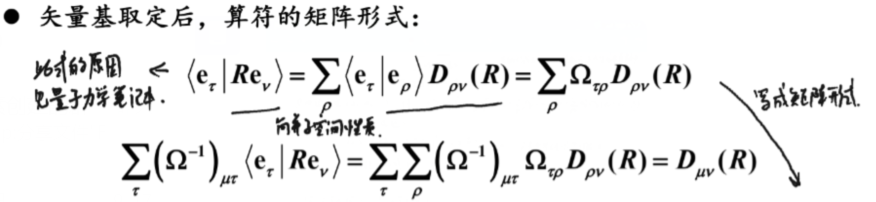
矩阵形式：
这是未选择正交归一矢量基时。
若选择正交归一的矢量基，

由（5）知，算符R在矢量基{ $\e_{μ}$ }中的矩阵表示：

6.共轭算符

在1.2节的4.中，已经定义了共轭矩阵：先转置再取复共轭。
注意只有这种说法：算符R的共轭算符为 $R^{†}$ 。

注意以上算符R的共轭算符 $R^{†}$ 的矩阵形式是在未选择正交归一矢量基时。
若在正交归一的基中，从上面推导知，此时，有结论：算符R的共轭算符 $R^{†}$ 的矩阵形式等于算符R的矩阵形式的共轭，即 $X (R^{†}) = D^{†} (R)$ ，其中共轭矩阵 $D^{†} (R)$ 即对 $D (R)$ 先转置再取复共轭。

在1.2节的4.中，已经定义了共轭矩阵：先转置再取复共轭，这是共轭矩阵的定义，与取不取正交归一的基无关。

其实就是厄米共轭。

1.6节幺正矩阵、厄米矩阵、正交矩阵、实对称矩阵

1.幺正矩阵

幺正矩阵的定义：

幺正矩阵的性质：

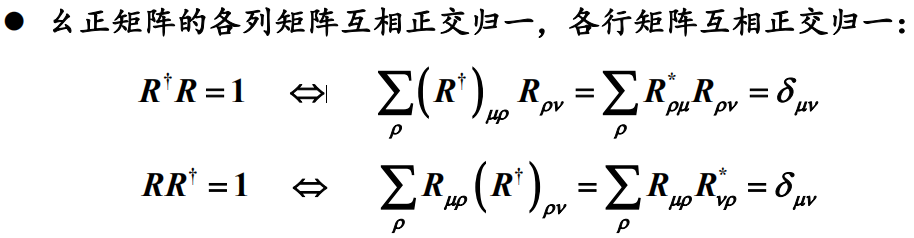
以上也就是秦静线性代数书125至128页如何相似对角化的过程

2.厄米矩阵

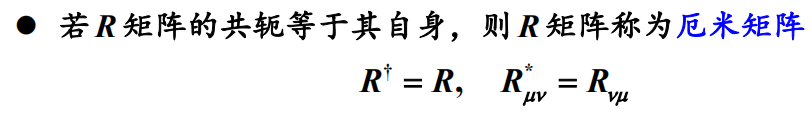
1.2节中说了：非奇异矩阵：行列式不为零的方矩阵，故

3.正交矩阵和实正交矩阵

定义：

性质：

4.实对称矩阵

定义：实的厄米矩阵称为实对称矩阵
由于厄米矩阵：，即先转置再取复共轭后与R相等，但由于是实的，故取复共轭无效，故：

同时，由于是实的，故也有：
。
即数学中的定义：
实对称矩阵：如果有n阶矩阵A，其矩阵的元素都为实数，且矩阵A的转置等于其本身（aij=aji），(i,j为元素的脚标），则称A为实对称矩阵。
实对称矩阵的性质：

1.7节矩阵的直乘

直乘的性质

1）直乘矩阵的维数等于因子矩阵维数的乘积。

2）直乘矩阵的迹：

3）设矩阵X1和X2维数相同, 矩阵Y1和Y2维数相同，则：

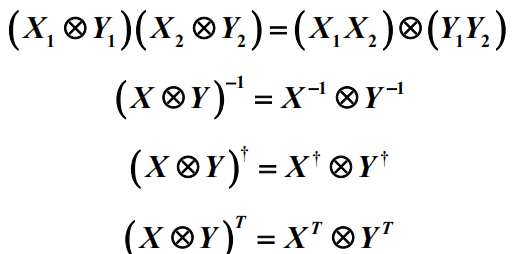
3）直积后的行列式

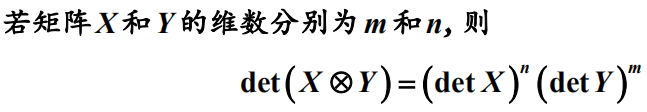
4）直积后的导数

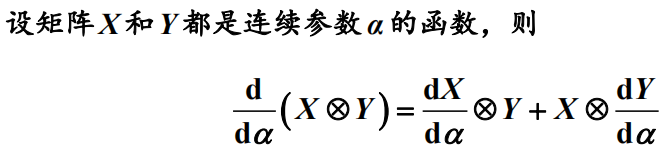
5）直积没有交换律

posted @ 2021-07-16 16:43 初心如磐使命在肩！阅读(2824) 评论(1) 编辑收藏举报

刷新页面返回顶部

yuan

求真务实,在科研中有针对性地研究有应用价值的方向,面向国家需求! gcdy的意志是钢铁！书山有路勤为径，学海无涯苦作舟

物理学中的群论 第一章 线性代数