霍尔效应、电导率

1）霍尔效应电导率（6）、电阻率（7）：
2）以上是电子情况。对于一般情况（包括电子、空穴）：$q=\pm e$
3）二能带半经典模型
4）注：hall效应的实验等更多介绍见datta量子输运书23-25页。必须复习

TOC

注意以下的e只表示电荷量大小。电子电荷量：-e，空穴电荷量：+e.



：

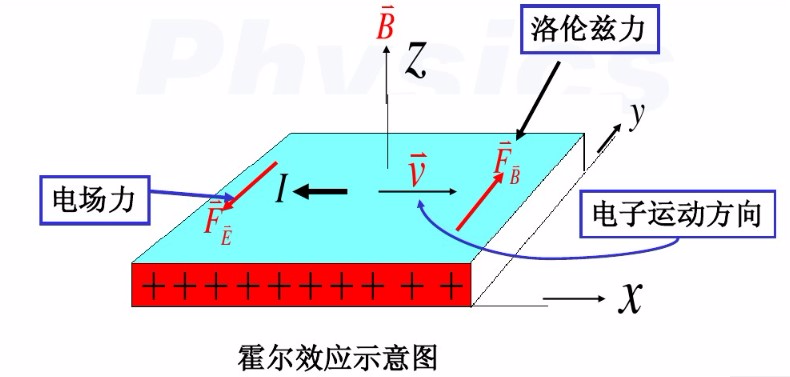
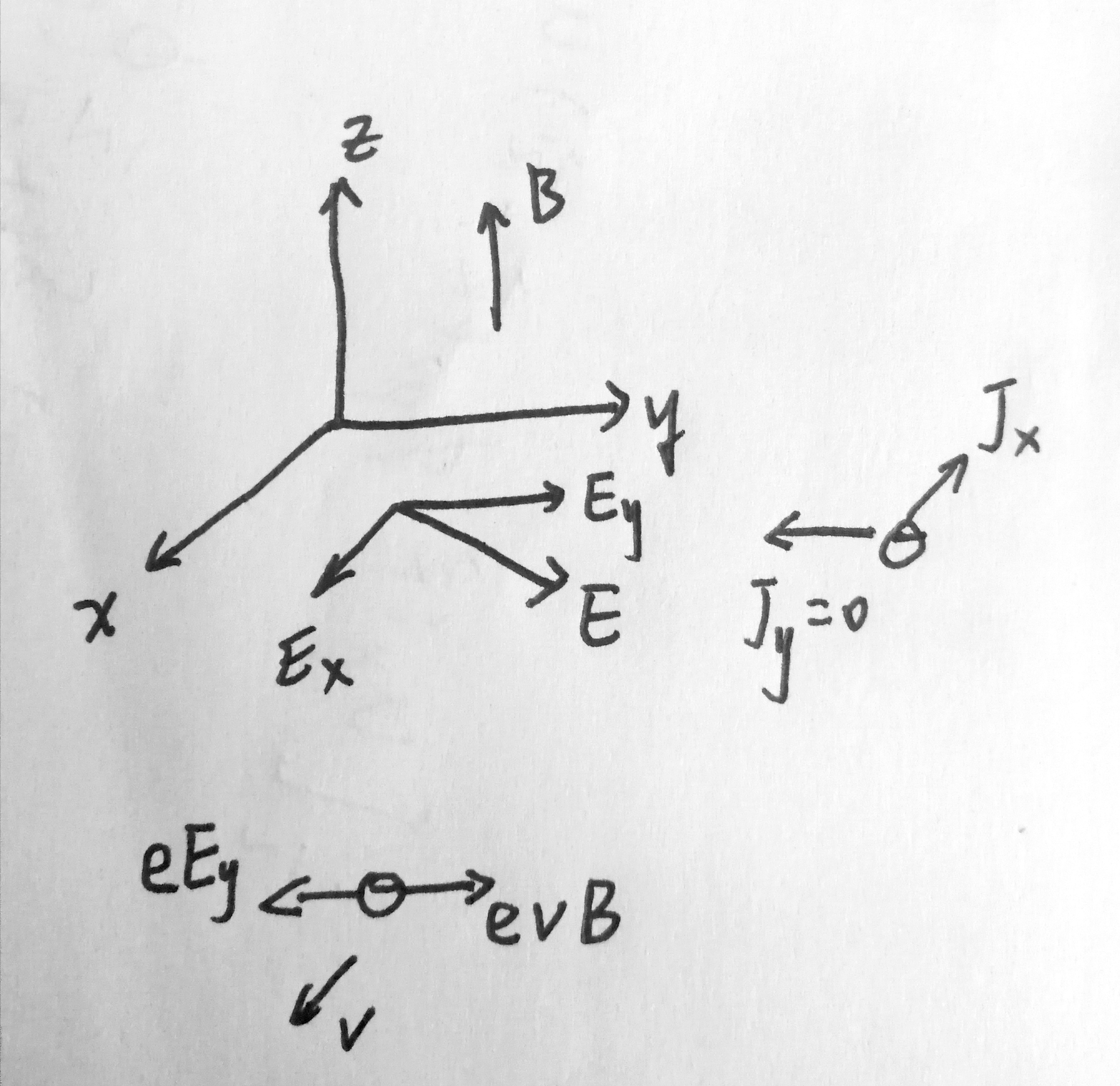
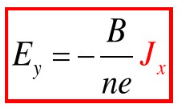
定义霍尔系数：

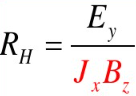
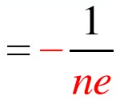
电子浓度越低，霍尔系数越大，霍尔效应越明显.（因为霍尔电场越大）
可以通过测量霍尔系数来检验金属自由电子气体模型的正确性.


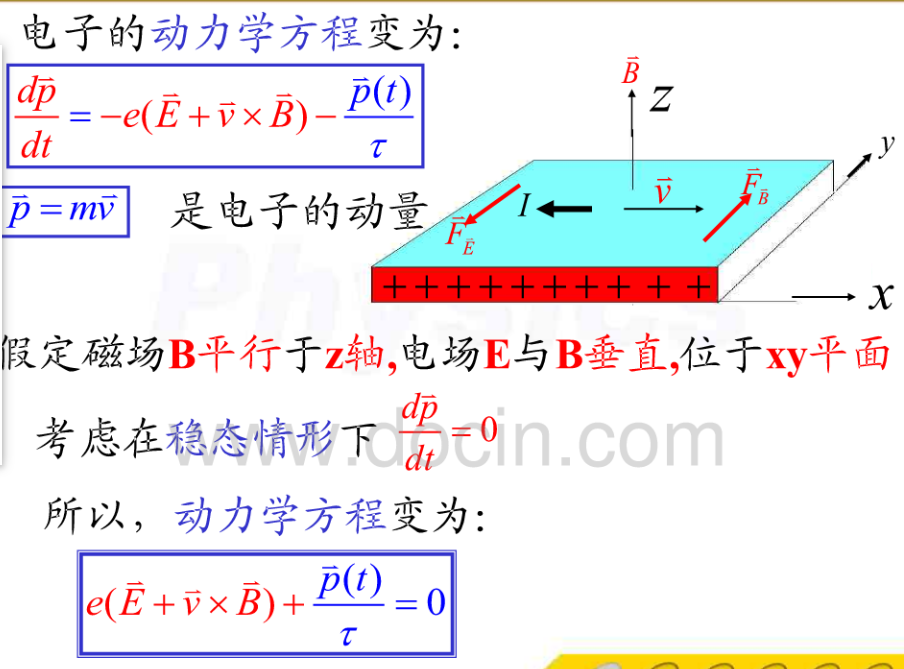
稳态即电子速度$\overrightarrow{v}$恒定。

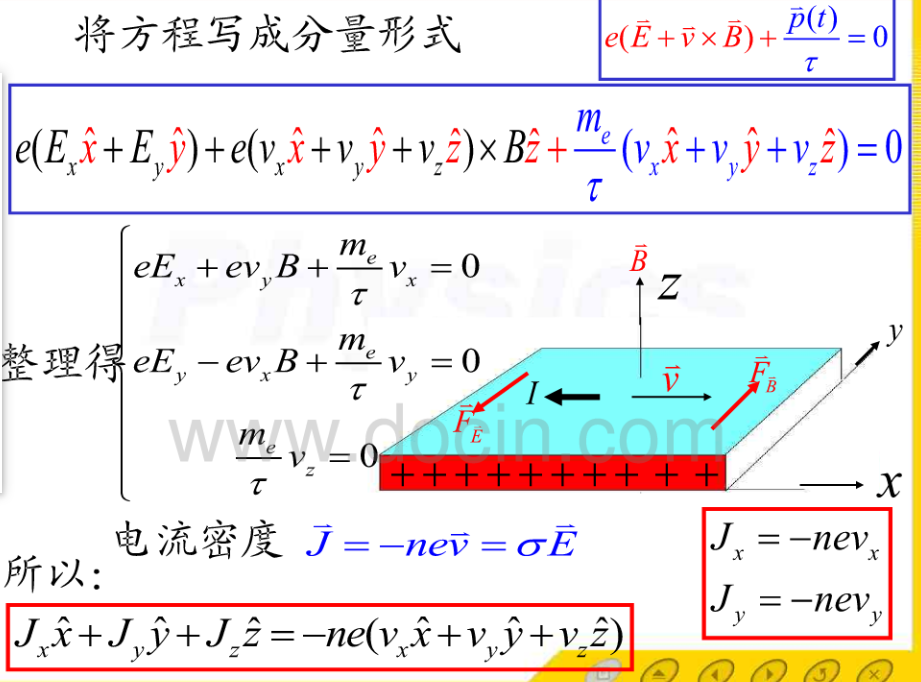
1）霍尔效应电导率（6）、电阻率（7）：

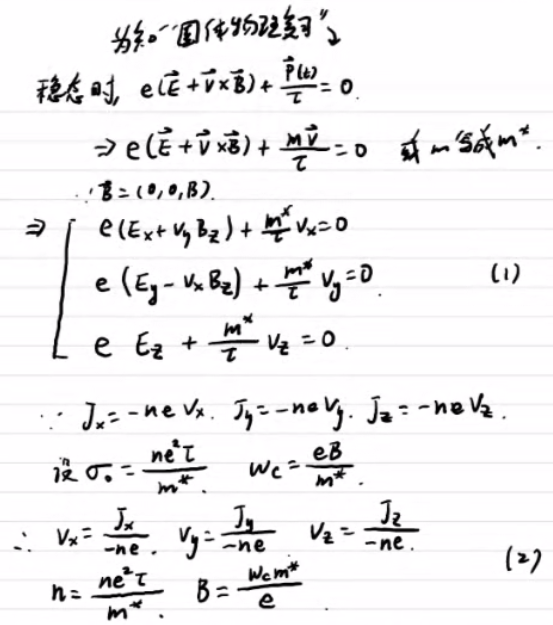
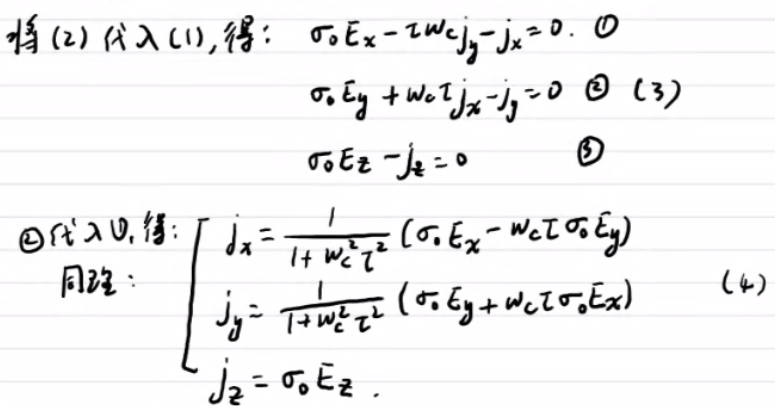
注意二阶矩阵取逆的公式：${\left(\begin{array}{ll}a& b\\ c& d\end{array}\right)}^{-1}=\frac{1}{ad-bc}\left(\begin{array}{cc}d& -b\\ -c& a\end{array}\right)$

（5）中有：磁-电导张量：

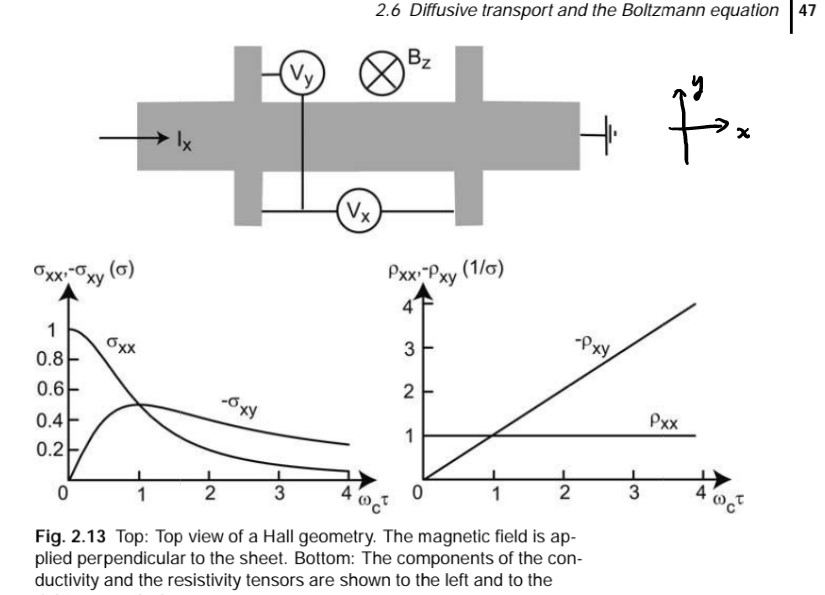
以上来自Heinzel的书。

北大固体物理书中，通过玻尔兹曼方程证明了：

$$\sigma =\frac{n{e}^2\tau }{m^{\ast }}=ne\mu$$

其中电子迁移率定义为： $\mu \equiv e\tau /m^{\ast }$. 利用此式可以知道：${\omega }_c\tau =\frac{e\tau }{m^{\ast }}B=\mu B$，将其代入（6），得：霍尔效应电导率：

$$\begin{array}{}\text{(8)}& \sigma =\frac{{\sigma }_0}{1+(\mu B{)}^2}\left(\begin{array}{cc}1& -\mu B\\ \mu B& 1\end{array}\right)\end{array}$$

2）以上是电子情况。对于一般情况（包括电子、空穴）：$q=\pm e$

定义$\tilde{\mu }=\frac{q\tau }{m^{\ast }}=\mathrm{sgn}(q)\mu$

其中sgn(q)表示q的符号。注意此公式和电子迁移率$\mu$不同，对电子，q=-e，$\tilde{\mu }=\frac{-e\tau }{m^{\ast }}=-\mu$

可以证明电导率：

$$\sigma =\frac{{\sigma }_0}{1+(\mu B{)}^2}\left(\begin{array}{cc}1& \tilde{\mu }B\\ -\tilde{\mu }B& 1\end{array}\right)$$

其中${\sigma }_0=\frac{n{e}^2\tau }{m^{\ast }}$
电阻率：

$$\mathit{\rho }={\rho }_0\left(\begin{array}{cc}1& -\frac{q\tau }{m^{\ast }}B\\ \frac{q\tau }{m^{\ast }}B& 1\end{array}\right)=\left(\begin{array}{cc}{\rho }_0& -\frac{B}{nq}\\ \frac{B}{nq}& {\rho }_0\end{array}\right)$$

其中${\rho }_0=\frac{1}{{\sigma }_0}=\frac{m^{\ast }}{n{e}^2\tau }$

定义霍尔系数：

$$\begin{array}{}\text{(9)}& R_{\mathrm{H}}=\frac{{\rho }_{yx}}{B}\end{array}$$

根据此式和（7）可以得到，对电子，霍尔系数$R_{\mathrm{H}}=-\frac{1}{ne}$，对空穴，霍尔系数$R_{\mathrm{H}}=\frac{1}{ne}$

此小节的这些定义，比如霍尔系数（9），都是介观课老师ppt中写的

3）二能带半经典模型

$$\begin{array}{l}{\sigma }_i(B)=\frac{{\sigma }_i}{1+{\mu }_i^2{B}^2}\left(\begin{array}{cc}1& {\tilde{\mu }}_{i}B\\ -{\tilde{\mu }}_{i}B& 1\end{array}\right),i=1,2\\ {\sigma }_i=n_{i}e{\mu }_i=\frac{n{e}^2{\tau }_i}{m_i^{\ast }},R_i=\frac{1}{n_i{q}_i}\\ \mathbf{J}={\mathrm{J}}_1+{\mathrm{J}}_2=({\sigma }_1+{\sigma }_2)\mathbf{E}\Rightarrow \mathit{\sigma }={\sigma }_1+{\sigma }_2\\ \mathit{\rho }(B)={\mathit{\sigma }}^{-1}=\left(\begin{array}{cc}{\rho }_{\mathrm{x}\mathrm{x}}& -R_{\mathrm{H}}B\\ R_{\mathrm{H}}B& {\rho }_{\mathrm{x}\mathrm{x}}\end{array}\right)\end{array}$$

两个能带情况，其电导率就是直接相加。
二能带模型的一个特例：
$\mathit{\sigma }(B)=\frac{{\sigma }_1}{1+{\mu }_1^2{B}^2}\left(\begin{array}{cc}1& {\tilde{\mu }}_{1}B\\ -{\tilde{\mu }}_{1}B& 1\end{array}\right)+\frac{{\sigma }_2}{1+{\mu }_2^2{B}^2}\left(\begin{array}{cc}1& {\tilde{\mu }}_{2}B\\ -{\tilde{\mu }}_{2}B& 1\end{array}\right)$
弱场极限下:

$$\begin{array}{rl}\mathit{\sigma }(B)& \simeq {\sigma }_1\left(\begin{array}{cc}1& {\tilde{\mu }}_{1}B\\ -{\tilde{\mu }}_{1}B& 1\end{array}\right)+{\sigma }_2\left(\begin{array}{cc}1& {\tilde{\mu }}_{2}B\\ -{\tilde{\mu }}_{2}B& 1\end{array}\right)\\ & \simeq \left(\begin{array}{cc}{\sigma }_1+{\sigma }_2& ({\sigma }_1{\tilde{\mu }}_1+{\sigma }_2{\tilde{\mu }}_2)B\\ -({\sigma }_1{\tilde{\mu }}_1+{\sigma }_2{\tilde{\mu }}_2)B& {\sigma }_1+{\sigma }_2\end{array}\right)\end{array}$$

故：${\rho }_{xx}=\frac{1}{{\sigma }_1+{\sigma }_2}、R_{\mathrm{H}}=\frac{{\sigma }_1{}^2{R}_1+{\sigma }_2{}^2{R}_2}{{({\sigma }_1+{\sigma }_2)}^2}$
强场极限：
可以证明：二能带半经典输运模型的两个特例:
1) 强场极限下 (即 ${\mu }_{1}B\gg 1,{\mu }_{2}B\gg 1$ ), 纵向电阻率和霍尔
系数分别趋近 ${\rho }_{xx}=\frac{{\sigma }_1{R}_1^2+{\sigma }_2{R}_2^2}{{\sigma }_1{\sigma }_2{(R_1+R_2)}^2},R_H=\frac{R_1{R}_2}{R_1+R_2}$
2) 对于电子和空穴浓度相等的半金属 (i. e. $R_1+R_2=0)$,
二者可写为: ${\rho }_{xx}=\rho (1+{\mu }_1{\mu }_2{B}^2),R_H=\frac{R_1{\sigma }_1^2+R_2{\sigma }_2^2}{{({\sigma }_1+{\sigma }_2)}^2}$.

二能带模型的另一个特例：半金属：
$n=p$ 霍尔系数满足 $:R_1+R_2=0$
${\rho }_{xx}(B)=\rho (1+{\mu }_1{\mu }_2{B}^2)$ 抛物线型磁电阻

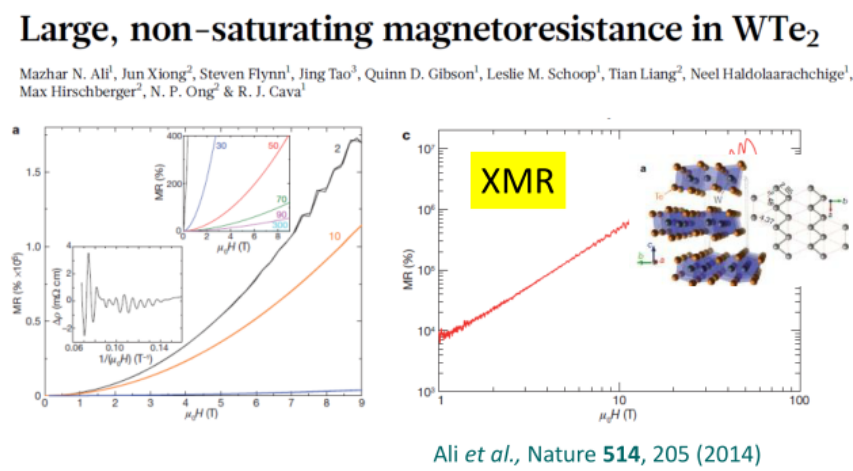
4）注：hall效应的实验等更多介绍见datta量子输运书23-25页。必须复习

---

$$参考资料$$

1.李永庆老师介观物理课件。并在此声明：以上许多内容来自李老师介观物理课的课件，在此我只是写个笔记
2.孙会元固体物理课件：https://www.docin.com/p-1115187674.html
3.Thomas Heinzel - Mesoscopic Electronics in Solid State Nanostructures-Wiley-VCH (2007)
4.阎守胜固体物理基础书