a short course书第3章 极化和贝里相位

3.1 The Rice-Mele Model
3.2 Wannier States in the Rice-Mele Model
3.2.1 Wannier态的定义性质
3.2.2 Wannier态是Bloch本征态的空间反演傅立叶变换
3.2.3 万尼尔中心等同于贝里相位
3.2.4 使用投影位置算符的Wannier态
在N趋于无穷的热力学极限下，投影位置算符${\hat{X}}_P$的本征态形成Wannier态。
3.3 空间反演对称性和极化
3.3.1 由于反演对称性的威尔逊圈的量子化
习题
此章有许多不懂

TOC
能带绝缘体的体极化bulk polarization是一个棘手的概念。中性分子的极化很容易用组成系统的正负电荷中心的差异来定义。当我们试图将这个简单的概念应用到能带绝缘体的周期性体bulk上时(为简单起见，假设正原子核是固定的和局域的)，我们会遇到复杂的问题。负电荷的中心应根据完全占据的价带中的电荷密度来计算。然而，价带中的所有能量本征态在bulk中都是离域的，因此在这样一个状态下每个电子的电荷中心是不明确的。然而，绝缘体是可极化的，并通过电荷的重新排列来响应外部电场，这对应于bulk中的(微小)电流。因此，应该有一种方法来定义体极化。
在本章中，我们将证明对能带绝缘体，体极化如何能利用所谓的现代极化理论[23，27，28]来定义。电子对极化的贡献是多体电子态的特性，多体电子态是【完全占据价带的能量本征态的】斯莱特行列式。中心思想是使用不同的正交基来重写相同的斯莱特行列式，该基由局域态组成，即所谓的Wannier态。然后，可以很容易地评估处于Wannier态的每个电子对电荷中心的贡献，然后将其相加。
我们讨论最简单有趣的情况，即一维双能带绝缘体，其具有一个空能带和一个满带的情况，多能带的情况留待后面讨论。结果表明，Wannier态的电荷中心可以确定为布里渊区上满带的Berry相，也称为Zak相[38]。
有关电子波函数中Berry相的更完整和非常教学法的介绍，我们请读者参考Resta的一组课堂讲稿[26]。

3.1 The Rice-Mele Model

我们在本章中使用的玩具模型是Rice-Mele模型，它是从第1章的SSH模型中通过添加额外的交错格点势(onsite potential)获得的。N个晶胞的链上Rice-Mele模型的哈密顿量为

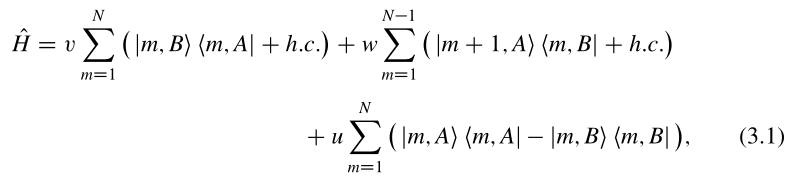
其中交错格点势$u$，晶胞内部跳跃幅度v和晶胞间跳跃幅度w都被假定为实数。N=4个格点的链的Rice-Mele模型的哈密顿量矩阵为

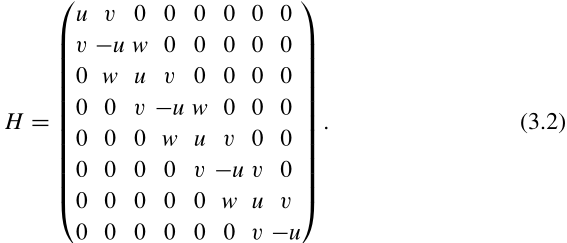
1.（3.1）的解释：在SSH模型中：这还不是体哈密顿量：

在此哈密顿量上加上交错的格点势u就得到（3.1），A原子上的格点势为u，B原子上的格点势为-u，这就是“交错”的势（这就是一个玩具模型，取这样的交错势没有为什么，是构造出来的），（3.1）中第三项的形式之所以能代表让一个电子位于格点的能量是因为：见SSH模型、sunkai紧束缚模型、固体理论课一维链中哈密顿量的来源、跳跃项.md

2.(3.2)证明：完全类似为知SSH模型中这种哈密顿量矩阵形式的证明过程，没时间，证明省略。

3.2 Wannier States in the Rice-Mele Model

能带绝缘体的体能量本征态在整个系统中是离域的（类似固体物理中说的巡游电子）。我们以Rice-Mele模型的体哈密顿量为例，即N个晶胞构成的环的模型。与第1.2节SSH模型的情况一样，能量本征态是调幅平面波布洛赫态，

其中

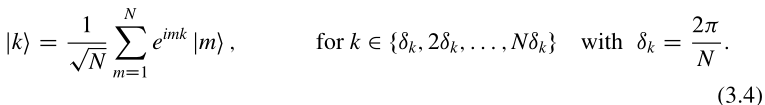
为简单起见，我们从本征态中省略了指标1。$|u(k)⟩$是体动量空间哈密顿量的本征态，

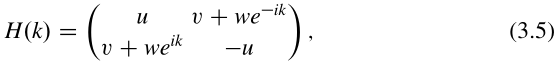
其本征值为.

rice-mele模型的计算过程完全类似SSH模型，我没时间，没算

布洛赫态$|\mathrm{\Psi }(k)⟩$散布在整个链上。它们横跨由投影算符定义的占据子空间

布洛赫态是调幅平面波，确实是散布在整个链。但什么是“由投影算符定义的占据子空间”？什么是子空间？这里是布洛赫态，而不是子空间的（这里的n是能带指标），（3.6）为什么会说“子空间”？

每个布洛赫本征态$|\mathrm{\Psi }(k)⟩$的相位可以随意设置。这些相位的变化，即规范变换，

给出了一组同样好的布洛赫态，对于$k={\delta }_k,2{\delta }_k,\dots ,2\pi$，具有任意一组相位$\alpha (k)\in \mathbb{R}$。利用这一自由度，原则上可以保证在$N\to \mathrm{\infty }$的热力学极限下，$|\mathrm{\Psi }(k)⟩$的分量（因为有$|\mathrm{\Psi }(k_1)⟩$等）是k的光滑、连续的函数。然而，这个规范可能不容易通过数值方法获得。因此，如果可能的话，我们更喜欢使用与规范无关的量，比如公式(3.6)中定义的占据子空间(occupied subspace )的投影算符（第一章贝里相位已经证明过投影算符是规范独立的）。

为什么说是k的连续光滑函数？因为虽然k是离散的，根据（3.4），但在热力学极限N趋于无穷，k近似就是连续的。但为什么通过这个规范变换就能使得$|\mathrm{\Psi }(k)⟩$可以是k的连续光滑函数？

3.2.1 Wannier态的定义性质

Wannier态$|w(j)⟩\in {\mathcal{H}}_{\text{external }}\otimes {\mathcal{H}}_{\text{internal }},$ with $j=1,\dots ,N,$由以下性质定义：

（3.8b）我觉得有些奇怪，为什么不是等于单位算符？难道万尼尔态不是完备的？

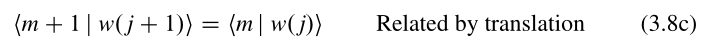
此公式我也觉得奇怪，这里的|m>应该是原子轨道，不知道为什么这样定义（3.8c）？我认为此式应该是根据（3.12）证明过程中得到的万尼尔函数表达式：，根据此表达式就直接验证了（3.8c）确实成立。

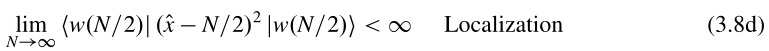
根据量子力学笔记本不确定关系一节知道：$⟨w(N/2)|(\hat{x}-N/2{)}^2|w(N/2)⟩$就是在万尼尔态$|w(N/2)⟩$时的x的分布宽度$\mathrm{\Delta }x$的平方.

但为什么分布宽度的平方小于无穷就是局域的？因为当N趋于无穷时，链长趋于无穷，只要分布宽度是个有限值，则相对于链长的量纲来说就是局域的。但为什么让N趋于无穷来进行说明?

with the addition in Eq. (3.8c) defined modulo N.

这句话我认为含义是：满足（3.8c）这个平移性质的j的指标的数量就定义了N的模.

对于（3.8d）的要求，即局域化要求，使用位置算符，

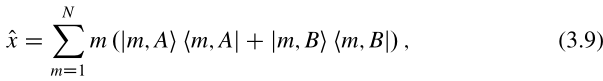
并涉及热力学极限N趋于无穷时的$|w(j)⟩$的性质，此性质并不容易去精确地定义。

在这种一维情况下，它可以变成指数的局域化的更严格的要求，即对于某个有限的局域化长度$\xi \in \mathbb{R}$，有.

这个关于局域化的讨论不懂，没时间
（3.9）证明：

3.2.2 Wannier态是Bloch本征态的空间反演傅立叶变换

由于布洛赫定理，所有能量本征态不仅在正则基$|m,\alpha ⟩$有平面波形式，其中$\alpha =A、B$，而且在Wannier基中都有平面波形式，

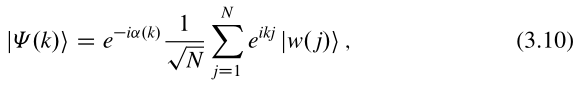
其中$\alpha (k)$是某相位因子。

我认为“$|m,\alpha ⟩$有平面波形式”说法是错误的，应该是中的才是平面波形式。
（3.10）类似SSH模型中的（1.8）：

这段话完全不懂，算了。

从（3.10），傅里叶空间反演变换得到万尼尔态：

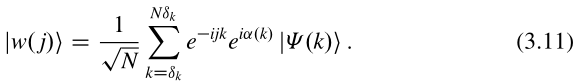
由于规范函数$\alpha (k)$不受约束，因此该形式仍有很大的自由度。这种自由度可以用来构建尽可能局域化的Wannier态。例如，如果找到一个光滑规范，其中在N趋于无穷的极限中，$e^{i\alpha (k)}|\mathrm{\Psi }(k)⟩$的分量是k的解析函数，那么由于傅立叶变换的性质，我们可以得到Wannier态的指数局域化。(更一般地，如果不连续首先出现在$|\mathrm{\Psi }(k)⟩$的第$l$阶导数中，则Wannier态的分量$|w(j)⟩$按$⟨m\mid w(j)⟩\propto |m-j{|}^{-l-1}$衰减.）

没时间证明万尼尔态的局域化。省略。

3.2.3 万尼尔中心等同于贝里相位

我们首先假设我们找到了一个连续的规范。Wannier态|w(0)>的中心可以用以下公式计算

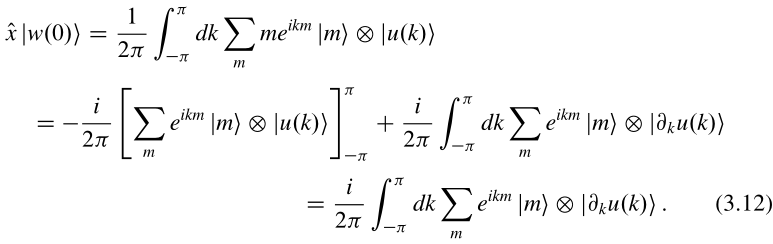
（3.12）证明:

我们发现Wannier态|w(j)>的中心是

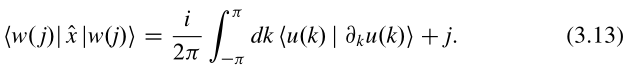
这个方程中的第二项表明，万尼尔态的中心是等间距的，彼此之间有一个晶胞的距离。（3.13）的第一项，即贝里相位再除以$2\pi$。此贝里相位是满带穿越布里渊区的贝里相位，参看(2.53)：${\gamma }_n(\mathcal{C})={\oint }_{\mathcal{C}}i⟨n(\mathbf{R})\mid {\mathrm{\nabla }}_{\mathbf{R}}n(\mathbf{R})⟩d\mathbf{R}$.（3.13）的第一项对应于对应于每个Wannier状态的均匀位移相同的量。

（3.13）证明：以后再说

我们将体电极化定义为跨越(span)布里渊区的【满带的Berry相位】，即公式(3.13)中的第一项，

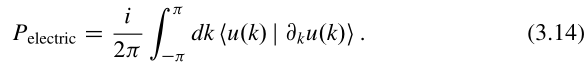
虽然我们上面推导的方法是直观的，但这仍然需要被证明这是一个一致的定义。从第二章可以清楚地看出，规范变换只能将体电极化改变一个整数。我们将在第五章中清楚地证明，这种极化在准绝热过程中的变化正确地再现了体电流。

“规范变换只能将体电极化改变一个整数”其实并不能从第二章贝里相位看出来，我写了一个此结论的证明：

得证。
此证明唯一的漏洞就是：我不知道为什么利用规范变换这一自由度可以保证在N趋于无穷的极限时，$|\psi (k)>$是k的光滑连续函数？即我不知道为什么（3.7）下面这一段话是为什么？

3.2.4 使用投影位置算符的Wannier态

一种数值上稳定、规范不变的寻找紧密局域化( tightly localized)的Wannier态集合的方式是使用幺正位置算符[28]，

这个算符很有用，因为它完全尊重环的周期性边界条件。$\hat{X}$的本征系统是由本征值为$e^{i{\delta }_{k}m}$的局域在晶胞m中的本征态组成的。因此，我们可以将处于态$|\mathrm{\Psi }⟩$时的位置的期望值与【$\hat{X}$期望值】的相位相关联，

（3.16）

这个公式作者没有解释，我试了也没有证明出来（3.16），作者的PPT中写：

此公式的原因有时间再查[1，28]

（3.16）中可能少了一个$Im$符号？或者没少？

此对数的实数部分能携带有关局域化程度的信息[1，28]。

这句话的理解应见[1,28]和量子光学中对相位算符的讨论，没时间

为了得到Wannier态，我们将幺正位置算符限制在满带上，定义

其中投影算符$\hat{P}$的表达式见（3.6）：$\hat{P}=\sum _{k\in BZ}|\mathrm{\Psi }(k)⟩⟨\mathrm{\Psi }(k)|$.

在N趋于无穷的热力学极限下，投影位置算符${\hat{X}}_P$的本征态形成Wannier态。

下面我们将说明，在N趋于无穷的热力学极限下，投影位置算符${\hat{X}}_P$的本征态形成Wannier态。
为简化算符${\hat{X}}_P$，考虑

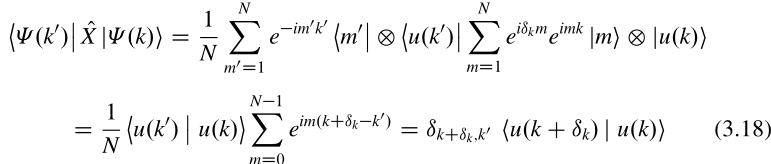
where ${\delta }_{k+{\delta }_k,k^{\mathrm{\prime }}}=1$ if $k^{\mathrm{\prime }}=k+{\delta }_k,$ and 0 otherwise.

其中$\frac{1}{N}\sum _{m=0}^{N-1}{e}^{im(k+{\delta }_k-k^{\mathrm{\prime }})}={\delta }_{k+{\delta }_k,k^{\mathrm{\prime }}}$的证明：根据为知傅里叶变换

知道：
得证。

利用（3.18）、（3.17），有：

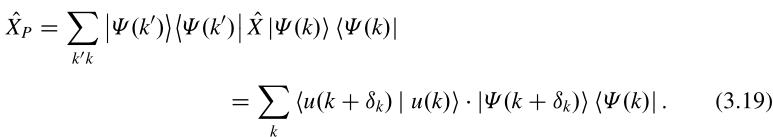
利用(3.19)的直接推论，我们可以求出${\hat{X}}_P$的本征值。即，将${\hat{X}}_P$提高到N次方，给出了一个算符，此算符正比于占据子空间中的单位算符:

其中比例常数$W\in \mathbb{C}$，其为：

这就是威尔逊圈。

请注意，W非常类似于离散Berry相位，不同之处在于$|W|\le 1$(尽管$\underset{N\to \mathrm{\infty }}{lim}|W|=1$)。

1.(3.20)证明：此式的证明是一个数学问题，我想了很久才证出来（开始想了很久没证出来，过了一天冷静下来之后又想了一小时才证出来），其实遇到问题不应该怕，不应该让情绪主导你，而应该冷静下来，仔细分析、慢慢思考有什么解决方法？这样才是解决问题之道！

注意（3.21）威尔逊圈的表达式中每个内积实际上都是一个数，可以任意换位置。
注意：以上（3.20）的证明过程中用到了rice-mele模型情况下，在N很大时，有布洛赫波函数的正交归一条件，此公式的证明：

2.“$|W|\le 1$(尽管$\underset{N\to \mathrm{\infty }}{lim}|W|=1$)”这个结论的证明：

因此，${\hat{X}}_P$的本征值谱由W的N次方根组成，

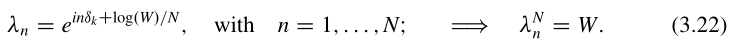
从（3.22）的证明过程知道，${\lambda }_n$的另一个表达式：
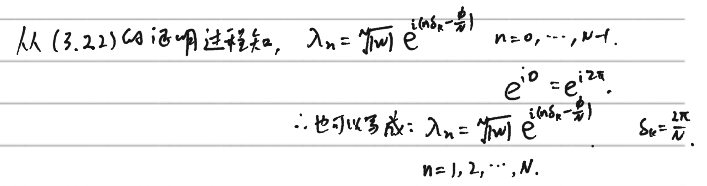（3.22.1）

从此知道：这些本征值具有相同的大小：$\left|{\lambda }_n\right|=\sqrt[N]{|W|}<1$，且相位$n{\delta }_k-\frac{\varphi }{N}$位于区间$[0,2\pi )$，各本征值的相位间隔排列，间隔为${\delta }_k$.          （3.22.2）

1.（3.22）证明：
先证明：$W=|W|e^{-i\varphi }$，其中$\varphi$是贝里相位。（作者ppt中有此结论）
根据（3.21）：$W=⟨u(2\pi )\mid u(2\pi -{\delta }_k)⟩\cdot \dots \cdot ⟨u\left(2{\delta }_k\right)\mid u\left({\delta }_k\right)⟩⟨u\left({\delta }_k\right)\mid u(2\pi )⟩$和环路的离散贝里相位的表达式：

相比可以知道$\varphi$是贝里相位。

此结论得证。
再根据数理方法书：

知道：

2.结论(3.22.2)证明：

因为根据（3.17）有：$⟨w(j)\left|{\hat{X}}_P\right|w(j)⟩=⟨w(j)|\hat{X}|w(j)⟩$，并根据（3.16）：$⟨x⟩=\frac{N}{2\pi }log⟨\mathrm{\Psi }|\hat{X}|\mathrm{\Psi }⟩$，故知道：${\lambda }_n$的大小告诉我们Wannier态的局域化性质，相位可以解释为位置期望值。

$⟨w(j)\left|{\hat{X}}_P\right|w(j)⟩=⟨w(j)|\hat{X}|w(j)⟩$中的$|w(j)>$取为${\hat{X}}_P$的本征态，其与万尼尔态有关系，见后面。
则：（此证明也有点疑问，（3.16）公式不一定对？（3.16）中有没有$Im$？还应该查，以后再说）

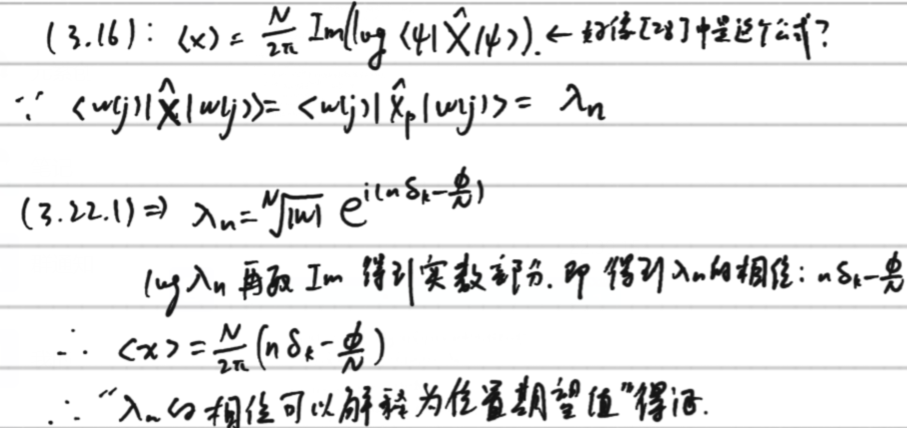
但“${\lambda }_n$的大小告诉我们Wannier态的局域化性质”此结论我不知道怎么证明，可能与（3.8d）有关？没时间

现在我们检查${\hat{X}}_P$的本征态是否满足Wannier态所要求的性质：式(3.8)。上面的关系${\left({\hat{X}}_P\right)}^N=W\hat{P}$表明${\hat{X}}_P$的本征矢量跨越在占据子空间(span the occupied subspace)。引入平移算符：$\hat{S}=\sum _{m=1}^N|(mmodN)+1⟩⟨m|\otimes {\mathbb{I}}_{\text{internal }}$。本征态通过平移联系在一起，因为

然而，本征态的正交性存在一个问题。我们将局域化的证明留给读者作为练习。

(3.23)等没时间证明。

对是否满足（3.8a）的说明：
投影的幺正位置算符${\hat{X}}_P$只在N趋于无穷的热力学极限下才是正规算符(Normal operator)。对于有限的N，它不是正规的，即它不能与它的伴随(adjoint)对易，因此它的本征态也不形成正交基。这可以看作是一个离散化错误。

没时间。
Normal operator
abstract: In mathematics, especially functional analysis, a normal operator on a complex Hilbert space H is a continuous linear operator N : H → H that commutes with its hermitian adjoint N*, that is:.
其中：Hermitian adjoint厄米共轭

abstract: In mathematics, specifically in functional analysis, each linear operator on a Hilbert space has a corresponding adjoint operator. Adjoints of operators generalize conjugate transposes of square matrices to (possibly) infinite-dimensional situations.

综上，${\hat{X}}_P$的本征态满足除了（3.8a）正交条件之外的Wannier态所要求的性质：式(3.8)
${\hat{X}}_P$的本征值${\lambda }_n$的大小告诉我们Wannier态的局域化性质，相位可以解释为位置期望值
${\hat{X}}_P$的本征值谱中的这些本征值具有相同的大小：$\left|{\lambda }_n\right|=\sqrt[N]{|W|}<1$，且相位$n{\delta }_k-\frac{\varphi }{N}$位于区间$[0,2\pi )$，各本征值的相位间隔排列，间隔为${\delta }_k$

3.3 空间反演对称性和极化

对于单分量、连续变量波函数$\mathrm{\Psi }(r)$，关于原点的反演(也称为宇称)具有效果：$\mathrm{\Psi }(r)\to \hat{\mathrm{\Pi }}\mathrm{\Psi }(r)=\mathrm{\Psi }(-r)$。表示反演的幺正算符$\hat{\mathrm{\Pi }}$的两个重要性质是：${\hat{\mathrm{\Pi }}}^2=1,$ and $\hat{\mathrm{\Pi }}{e}^{ikr}=e^{-ikr}$。如果$\hat{\mathrm{\Pi }}\hat{H}{\hat{\mathrm{\Pi }}}^{†}=\hat{H}$，则哈密顿量具有反演对称性。
在将空间反演算符推广到具有内部自由度的固体物理晶格模型时，我们必须记住两件事。
首先，在有限样本中，边缘一定会破坏关于原点的反演对称性(除了非常精细调整的样本制备)。因此，我们只关心体bulk的空间反演对称性，并要求它使得$|k⟩\to |-k⟩$。
其次，我们所考虑的晶格模型的每个晶胞也有其内部的希尔伯特空间，其会受到空间反演的影响。这包括自旋分量(未受空间反演影响)和轨道类型的变量(受空间反演影响)。一般而言，我们用一个幺正算符$\hat{\pi }$表示空间反演对内部Hilbert空间的作用。$\hat{\pi }$独立于晶胞。
在晶格模型的体哈密顿量上，空间反演算符用$\hat{\mathrm{\Pi }}$表示。它作用于${\mathcal{H}}_{\text{internal }}$的算符用$\hat{\pi }$表示。

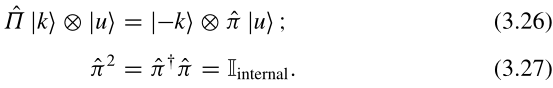
（3.27）是因为两次作用，不变。但为什么${\hat{\pi }}^{†}=\hat{\pi }$？因为空间反演算符是厄米算符，原因见曾书量子力学卷一5.4.3节。

空间反演算符对体动量空间哈密顿量的作用可以使用其定义读出，

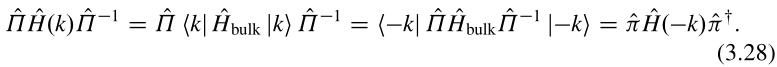
（3.28）怎么证明？以后再说

如果存在幺正、厄米算符$\hat{\pi }$作用于内部空间，以至于

则晶格模型在体上具有空间反演对称性。

根据为知时间反演对称性、空间反演对称性对布洛赫波、贝里矢势、贝里曲率的作用中曾书卷二（7.2.11）、（7.2.32）知道，应该是证明了$\hat{\mathrm{\Pi }}\hat{H}{\hat{\mathrm{\Pi }}}^{-1}=\hat{H}$则就证明了系统有空间反演对称性。但是，这里证明了$\hat{\mathrm{\Pi }}\hat{H}(k){\hat{\mathrm{\Pi }}}^{-1}=\hat{H}(k)$，为什么这说明了系统有空间反演对称性？没时间

如果所有被占据的能带在能量上都可以绝热分离开，那么我们可以聚焦在一个能带上，用波函数$|u(k)⟩$，空间反演对称性会有一个简单的结果。-k和k处的本征态由下式关联

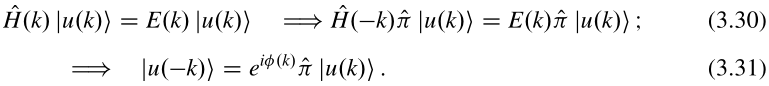
对于波数$k=0$ and $k=\pi$，即所谓的时间空间反演不变动量点（见changmingze的讲义），这意味着它们是具有确定的宇称的态，

不会证明，没时间

3.3.1 由于反演对称性的威尔逊圈的量子化

现在我们重写空间反演对称一维哈密顿量的能带的Wilson圈W，假设我们有一个离散化成2M个k状态，用$j=-M+1,\dots ,M$标记，为

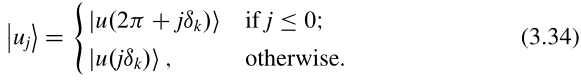
我们使用公式(3.31)，其形式为

空间反演对称的一维绝缘体能带的Wilson圈W只能取值±1。我们以M=3时为例说明这一点。

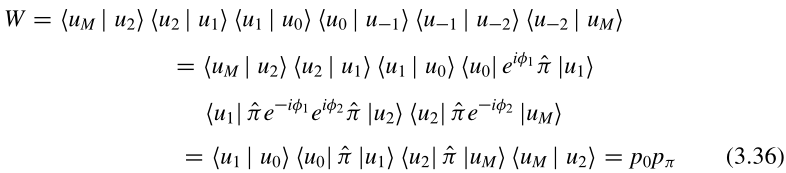
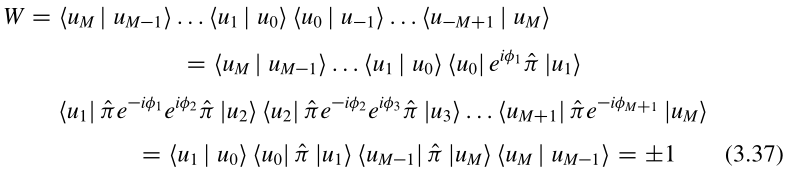
关于威尔逊圈的陈述可以使用公式(3.14)翻译为体极化。空间反演对称的一维绝缘体的每个能带对体极化有0或1/2的贡献。

根据和
可以知道（3.36）第一行确实是威尔逊圈的表达式。

（3.36）、（3.37）没时间证。

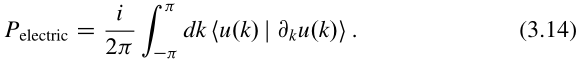
威尔逊圈类似离散贝里相位。这样就可以和（3.14）建立联系？

”空间反演对称的一维绝缘体的每个能带对体极化有0或1/2的贡献"怎么证？

习题

此章有许多不懂