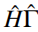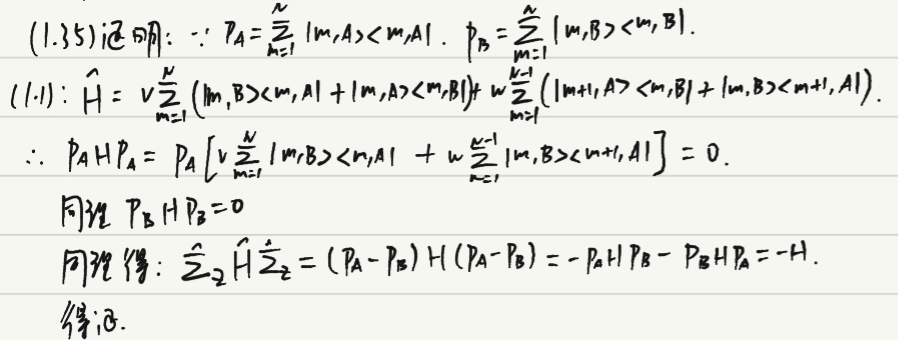##a short course书 第1章 SSH模型
a short course拓扑绝缘体 第1章 SSH模型
1.3节 边界态
1.完全二聚化极限
a.完全二聚化极限中的bulk有平带
b.完全二聚化极限中的边界态可以是零能态
2.远离完全二聚化极限
1.4节 手征对称性
a.没有幺正对称性
b.另一种不同类型的对称性
1.4.1 手征对称性对能量本征态的影响
子晶格对称性
对称谱
a.若,
b.若E=0,
1.4.2 SSH模型的子晶格投影和手征对称性
1.4.3 手征对称性的影响:SSH模型的体缠绕数
缠绕数是重解(重根)的个数
缠绕数是一个积分
SSH模型的缠绕数
1.5节 边界态的数目是拓扑不变量
绝缘哈密顿量的绝热变形
哈密顿量的绝热等价
拓扑不变量
边界态的数目是拓扑不变量
SSH模型中的体-边界对应
1.5.1 畴壁上的束缚态
1.5.2 边界态的精确计算
边界态的杂化
1.6节 总结
重要:体-边界对应:我们能使用体拓扑不变量(缠绕数)去预测在边界的低能物理
 :
:
将这里算能带的方法的法1、法2都和李正中书328、329页紧束缚算能带的法二很类似(其实差不多)。








>注意这里假设不同格点的原子轨道相互正交是合理的,见经验紧束缚法、实空间紧束缚法 - 初心如磐使命在肩! - 博客园 (cnblogs.com)中:
以上两种方法不太便于理解。其实最简单、最好懂的方法是使用每个原胞中包含多个原子轨道情况下的经验紧束缚方法【见经验紧束缚法、实空间紧束缚法 - 初心如磐使命在肩! - 博客园 (cnblogs.com)】:

>
> >
>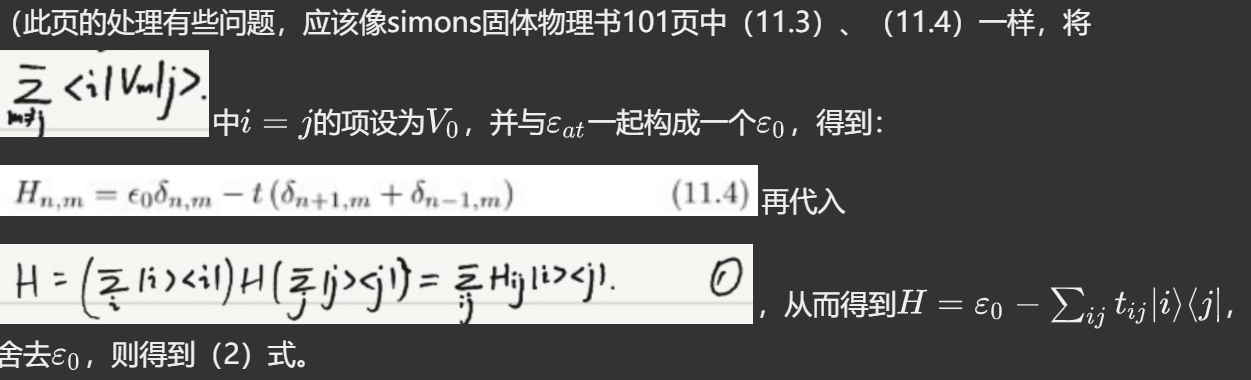
经验紧束缚法:

>注意在以上推导中利用了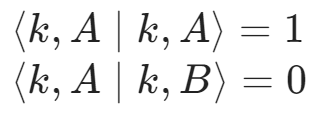 ,此公式可以通过近似假设不同轨道的原子波函数互相正交而得到,在经验紧束缚法、实空间紧束缚法 - 初心如磐使命在肩! - 博客园 (cnblogs.com)中解释过:
,此公式可以通过近似假设不同轨道的原子波函数互相正交而得到,在经验紧束缚法、实空间紧束缚法 - 初心如磐使命在肩! - 博客园 (cnblogs.com)中解释过:
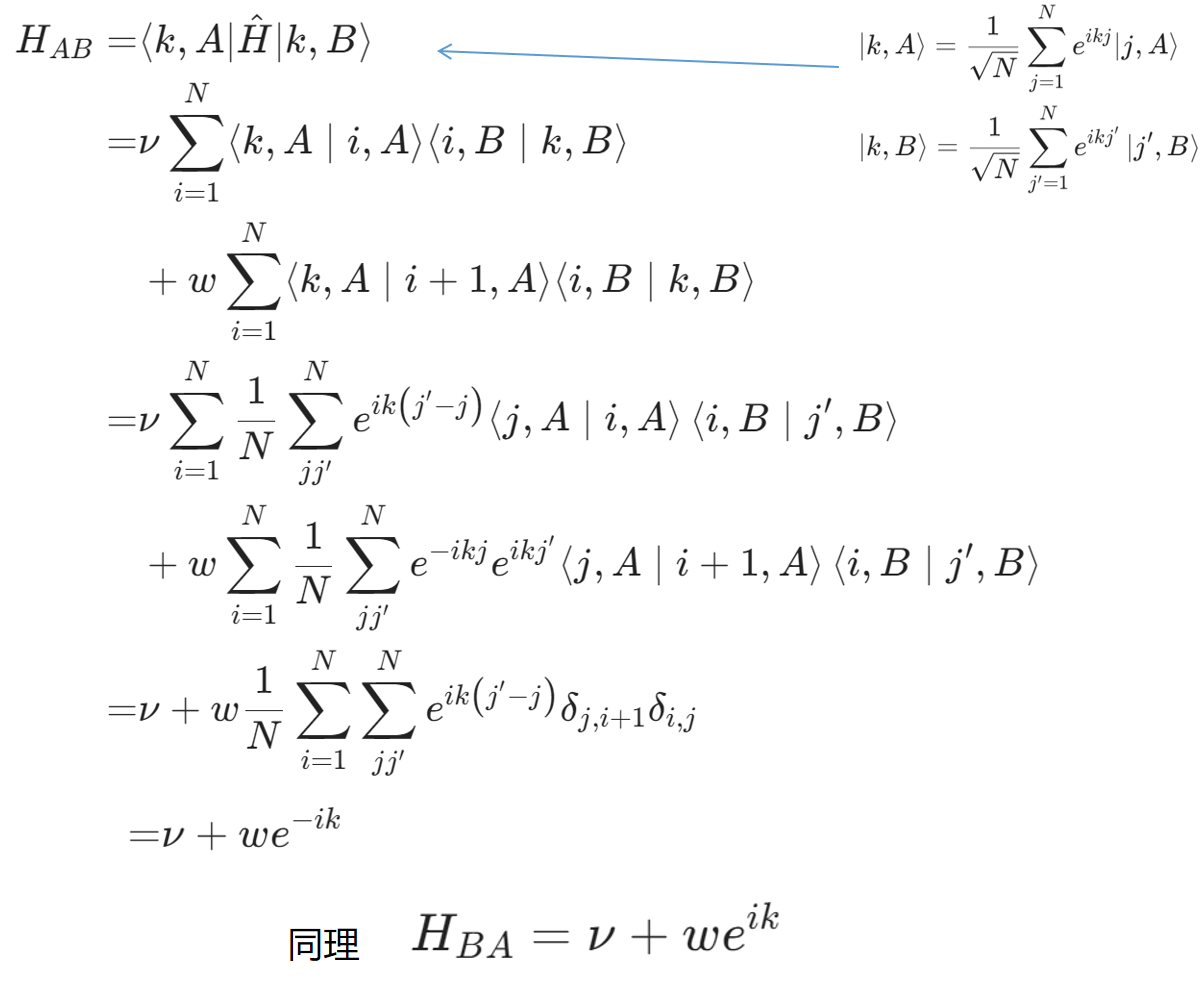

>以上方法是经验紧束缚法和实空间紧束缚法的杂糅。



1.3节 边界态
SSH哈密顿量不但有bulk部分,也有边界部分(称为边界)。bulk和边界之间的差别不是严格定义的。在大多数情况,bulk是平移不变的,但边界不是平移不变的。而且,我们能区别bulk state或edge state的能量本征态,通过它们在热力学极限下的行为来区别。我们将从所谓的完全二聚化极限开始,其中边界区域能明确地定义。然后我们离开这些极限,使用边缘态的实际定义。
1.完全二聚化极限
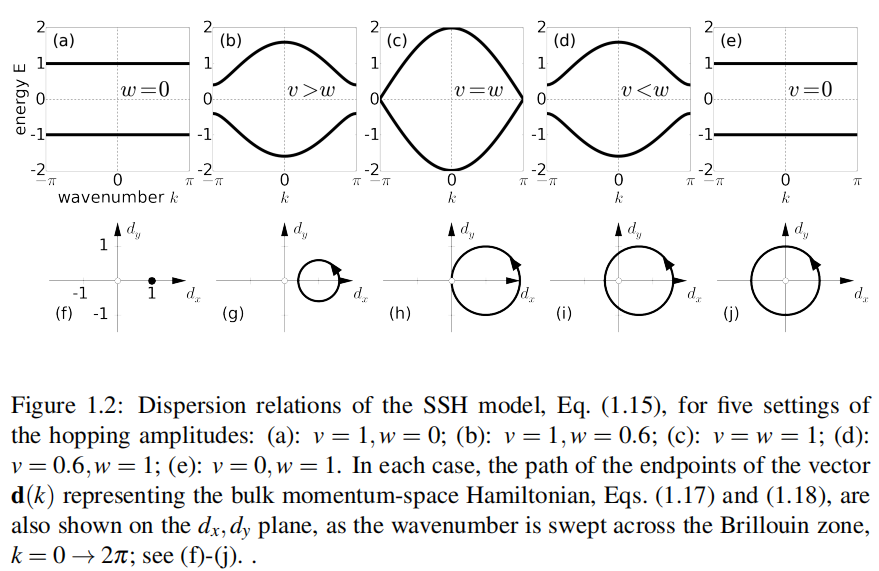
The ssh model becomes particularly simple in the two fully dimerized cases:if the intercell hopping amplitude vanishes and the intracell hopping is set to 1, v=1,w=0, or vice versa, v=0, w=1. In both cases the SSh chain falls apart to a sequence of disconnected dimers(一系列不连接的二聚物) as shown in Fig. 1.3。
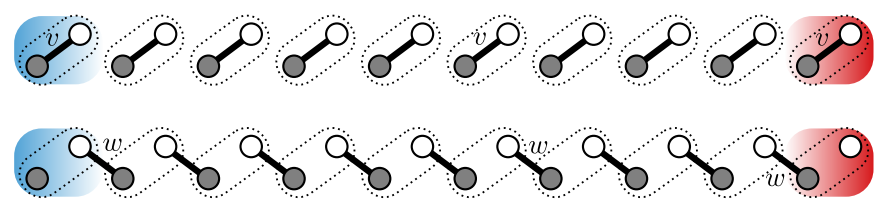
Figure 1.3:Fully dimerized limits of the Ssh model, where the chain has fallen ap disconnected dimers In the trivial case(top, only intracell hopping,v=l,w=0), every energy eigenstate is an even or an odd superposition of single-site basis states in the same unit cell. In the topological case, (bottom, only intercell hopping, v=0, w=1)dimers are shared between neighboring unit cells. Then there is a single isolated site on each edge, that must host one eigenstate(per edge), at zero energy, since there are no onsite potentials.(因为不会跳跃,而且势能取为零)
a.完全二聚化极限中的bulk有平带
在完全二聚化极限中,我们能为bulk哈密顿量选择一组能量本征态,此组能量本征态是限制在每单个二聚物中。
在v=1,w=0的情况,我们称为平庸的。

在v=0,w=1的情况,我们称为拓扑的。每个二聚物涉及两个相邻的晶胞。

在以上两种完全二聚化极限的情况,我们都能叠加以上定义的局域本征态(即(2)、(4)本征态)去组成布洛赫型能量本征态。
书中未证明
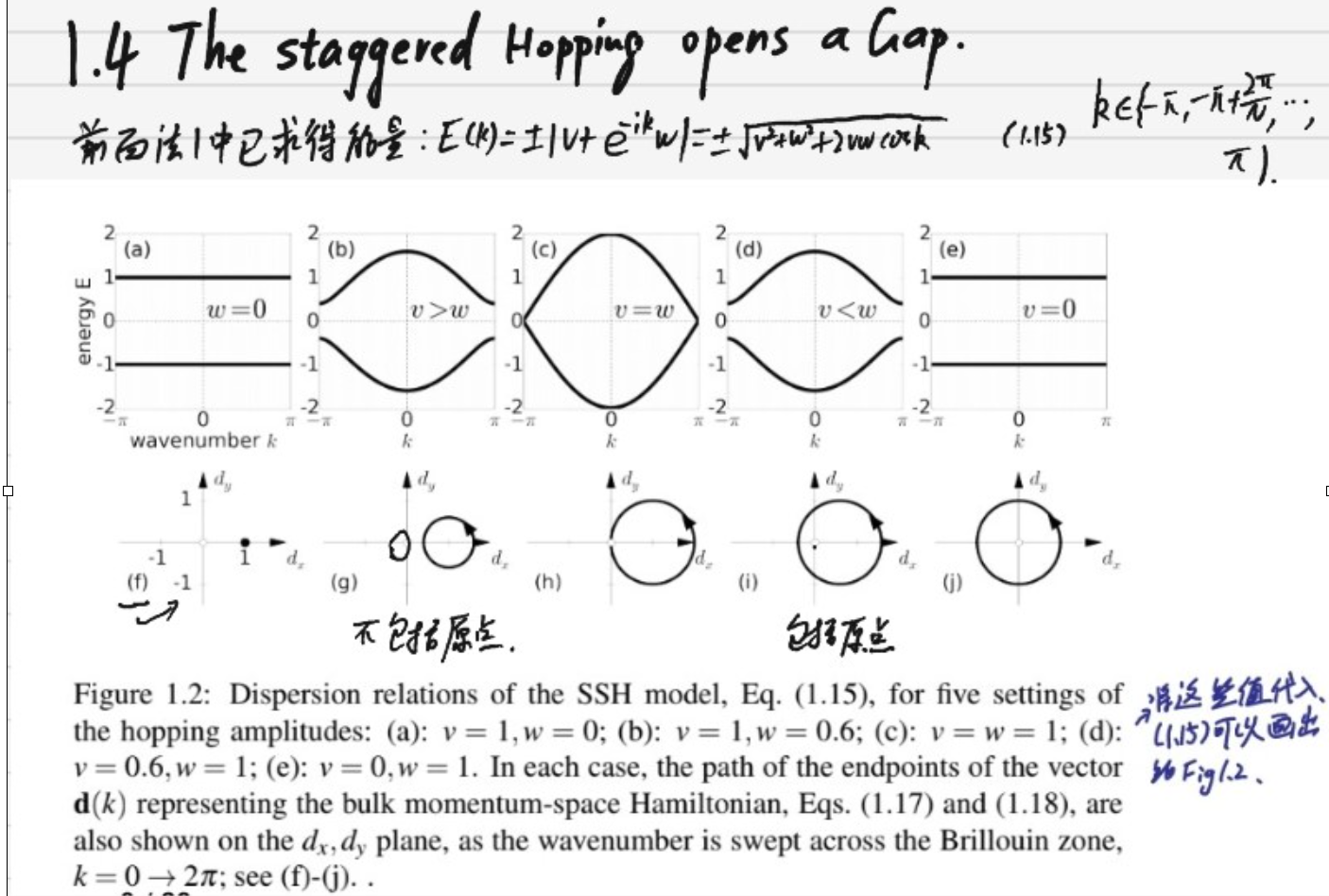
这些布洛赫本征态继承了相同的能谱, ,即我们有平带在这个情况,正如图1.2a和e。
,即我们有平带在这个情况,正如图1.2a和e。
由固体物理 布洛赫电子的准经典运动知:

对每个能带,群速度为0,故粒子不能沿着链运动。从物理上,由于v=0或w=0,粒子不能跳跃,故确实不能沿着链运动。
b.完全二聚化极限中的边界态可以是零能态
在平庸情况,v=1,w=0,SSH链的所有能量本征态由前面a部分的(2)给出。
而在拓扑情况,v-0,w=1,有比前面a部分的(4)更多的本征态。链的末端有单个在零能量的本征态,
 (1.21)
(1.21)

这两个本征态分别位于末端。它们的能量为零是因为其不能跳跃,只有势能,势能设为0(SSH模型哈密顿量中没考虑势能,设为0)。这些是边界态最简单的例子。
2.远离完全二聚化极限
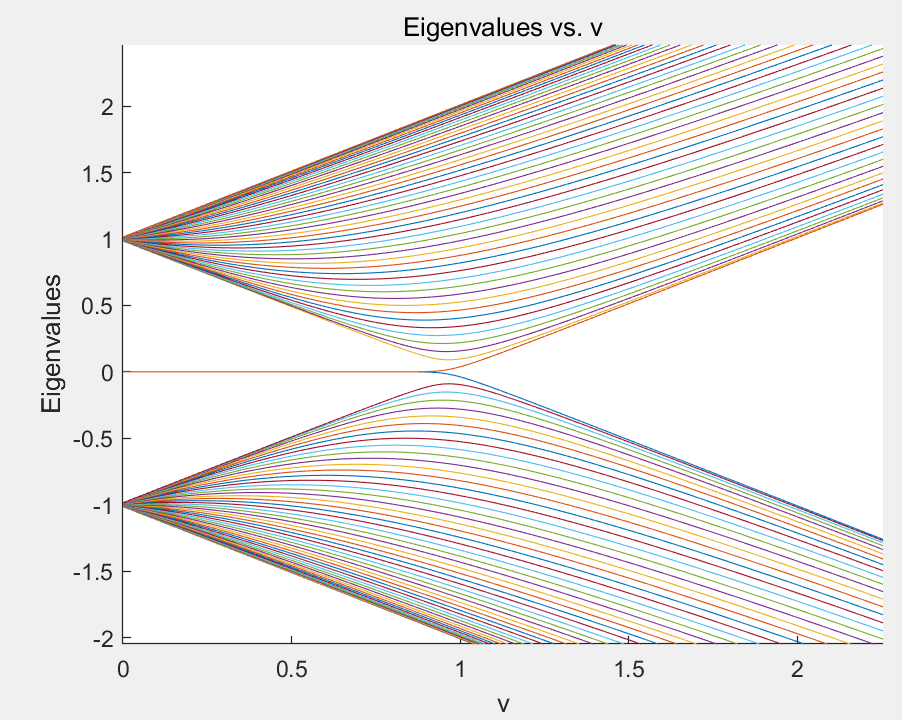
We now examine what happens to the edge states as we move away from the fully dimerized limit. To be specific, we examine how the spectrum of an open topological chain, v=0, w=l, of N= 10 unit cells changes, as we continuously turn on the intracell(胞内) hopping amplitude v. The spectra, Fig. 1.4a, reveal that the energies of the edge states remain very close to zero energy。
未证明
几乎为零能(即近零能)的边界态的波函数必须是指数局域在左/右边界,因为零能位于体能带能隙中,所以它不可能位于bulk中。
波函数的图见fig1.4b和c,揭示了几乎为零能的本征态是指数局域在左和右边界。 这是左、右边界态的指数地小重叠的结果。我们后面将在1.5.2节中证明,边界态能量也由这个重叠控制。并且是![]() 的量级,其中局域长度
的量级,其中局域长度![]() 。与这些边界局域近零能态相反,所有其他的态都是在整个链中是非定域化的,如图1.4d。
。与这些边界局域近零能态相反,所有其他的态都是在整个链中是非定域化的,如图1.4d。
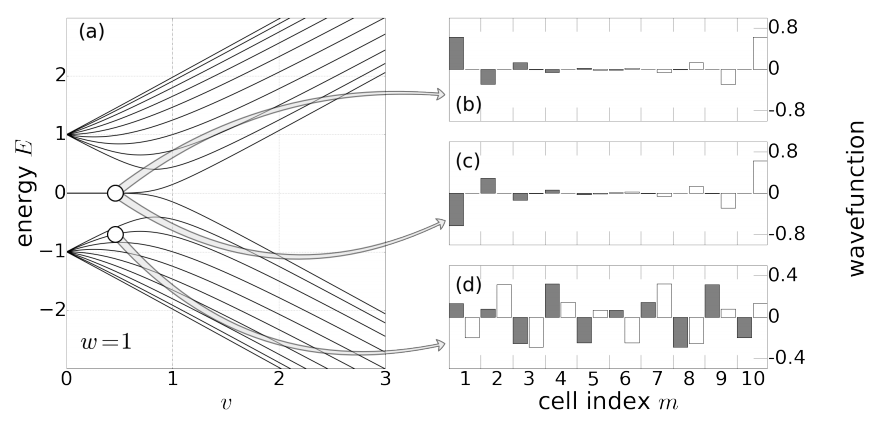
Figure 1. 4:Energy spectrum and wave functions of a finite-Sized SSH model. The number of unit cells is N=10.(a)Energy spectrum of the system for intercell hopping amplitude w= l as a function the intracell hopping amplitude v. v<1(v>1)corresponds to the topological(trivial) phases.(b)and(c) shows the wave functions of the hybridized edge states, while( d) shows a generic bulk wave function。b,c,d图中,黑色代表A格点,白色代表B格点。
v<1(v>1)corresponds to the topological(trivial) phases的原因:因为由图知,v<1时,有近零能边界态,故称为拓扑相,v>1时没有边界态,所以称为平庸相。

fig1.4的图怎么画出来的书中没说,后来参考了知乎拓扑凝聚态Chapter1. SSH(Su-Schrieffer-Heeger)模型, 绕数(Winding Number) - 知乎 (zhihu.com),就知道怎么画的:参考##a short course书 第1章 SSH模型 - 初心如磐使命在肩! - 博客园 (cnblogs.com) 中哈密顿量矩阵法,以及拓扑凝聚态Chapter1. SSH(Su-Schrieffer-Heeger)模型, 绕数(Winding Number) - 知乎 (zhihu.com)中mma代码,通过问cursor知道对应的matlab代码:
在Matlab中,脚本和函数应该分开存放,或者所有操作都应该在函数内部进行。我们可以将主要的操作部分封装成一个主函数,比如叫main,然后在这个主函数中调用其他函数。下面是修复后的代码,包括详细注释:function main % 主函数,执行程序的主要逻辑 N = 50; %所取的原胞的数量 end_val = 3; % 参数v的最大值 y = zeros(200, 2*N); % 初始化存储特征值的矩阵,注意由于哈密顿矩阵是2N维,故本征值也有2N个 % 计算特征值 for index = 1:200 v = index * end_val / 200; % 计算当前的v值,v是胞内hopping的强度 H_matrix = H(N, v, 1); % 计算哈密顿量, 胞间跃迁w=1 y(index, :) = sort(eig(H_matrix)); % 计算特征值并排序 end % 绘图 figure; hold on; for i = 1:2*N plot(linspace(0, end_val, 200), y(:, i)); end xlim([0, end_val]); ylim([-3, 3]); % 根据实际情况调整y轴范围 xlabel('v'); ylabel('Eigenvalues'); title('Eigenvalues vs. v'); hold off; end function b = basis(N, i, alpha) %N是原胞数量(函数中的局域变量),i是原胞指标,alpha是A或B,表示哪个原子 % 定义基底函数,就是原子轨道函数,与我博客中的哈密顿量矩阵法相同 b = zeros(1, 2*N); if alpha == 1 b(2*i-1) = 1; else b(2*i) = 1; end end function Hh = Hh(N, v, w) %v和w分别是胞内跃迁和胞间跃迁强度 % 定义哈密顿量的一半。注意,这里由于要使用的是博客中的哈密顿量,由于考虑边界态,所以使用开边界条件 Hh = zeros(2*N, 2*N); for m = 1:N Hh = Hh + v * (basis(N, m, 2)' * basis(N, m, 1)); %注意这里是外积 if m < N Hh = Hh + w * (basis(N, m+1, 1)' * basis(N, m, 2)); end end end function H = H(N, v, w) % 完整的哈密顿量 H_half = Hh(N, v, w); H = H_half + H_half'; %厄米共轭是先转置再取复共轭 end结果:当N=50时,
以上代码中哈密顿量的由来是:
不过由于这里考虑边界态,所以没有加上
这个周期条件。
【这里假设不同格点的原子轨道相互正交是合理的,原因见博客SSH模型】
注意这里是一个条带,所以根本没有波数k。
当纳米条所取的原胞数N越来越大时,得到的一系列离散的能量值(不过还是没有波数k),这些能量值会接近bulk哈密顿量得到的能带中所有能量的值。因为N越大,越接近bulk。
由fig1.4b和c知,边界态的重要性质:右边边界态只在B子晶格有非零分量(即右边边界态只在右边边界的几个晶胞中的B格点有非零分量),左边边界态只在A子晶格有非零分量。
我们将证明这些性质的一般性,并证明体缠绕数和边界态存在/缺失之间的联系,这称为体-边界对应。在SSH模型的情况,有一个重要性质:手征对称性。
1.4节 手征对称性
量子力学中,我们说一个哈密顿量有对称性是其由一个幺正算符来表示:
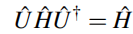 (1.22)
(1.22)
在一个对称性的情况,U和H能被同时对角化,因此,H没有矩阵元在U的两个不同本征值对应的本征态之间。这能被理解作为一个超级选择定则:如果我们将希尔伯特空间分成不同部分,即U的本征空间,这些本征空间是由对应的本征值标记的, then the dynamics as defined by H can be regarded separately in each sector.
最后这句话不知道什么意思
a.没有幺正对称性
如果我们限制自己到希空间的一部分,幺正对称性能简单地被设为消失。This is how we obtained the bulk momentum-space Hamil-tonian, in Sect. 1.2, where the symmetry was the lattice translation operator![]() , and the labels of the superselection (超级选择)sectors were the quasimomenta k。
, and the labels of the superselection (超级选择)sectors were the quasimomenta k。
在傅里叶变换后,晶格平移对称性在哈密顿量中不再显示。所以称为消失
b.另一种不同类型的对称性
“对称”这个词在凝聚态物理中也有不同的含义,例如手征对称性。如果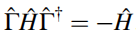 (1.23),则称此系统具有手征对称性。其中算符
(1.23),则称此系统具有手征对称性。其中算符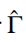 不仅是幺正的,还满足一些其他规则。右边的负号是重要的,后面会讨论。
不仅是幺正的,还满足一些其他规则。右边的负号是重要的,后面会讨论。
首先,为了排除通常的幺正对称性,手征对称性算符必须不仅是幺正的,而且是厄米的 此规则能简洁地写成:
此规则能简洁地写成: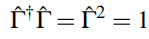 (1.24)
(1.24)
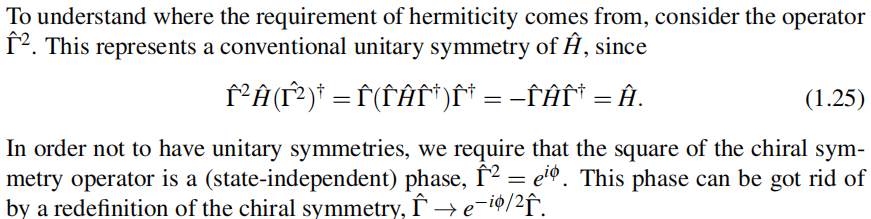
以上图片中的内容不懂,书中没说清楚
由张永德书112页,幺正算符的定义:可知(1.24)成立
第二,要求子晶格算符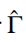 是局域的。假设系统由晶胞组成,在来自(不同晶胞)的格点之间的
是局域的。假设系统由晶胞组成,在来自(不同晶胞)的格点之间的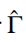 的矩阵元应该为零。在SSH链中,这意味着
的矩阵元应该为零。在SSH链中,这意味着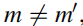 时,
时,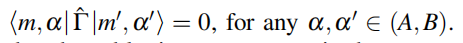 为了使事情简单,我们要求子晶格算符以相同的方式作用在每个晶胞中(即使严格来说这不是必要的),它的作用由一个幺正算符
为了使事情简单,我们要求子晶格算符以相同的方式作用在每个晶胞中(即使严格来说这不是必要的),它的作用由一个幺正算符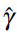 作用在一个晶胞的内部希空间来表示,即
作用在一个晶胞的内部希空间来表示,即
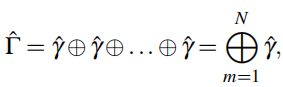 (1.26)
(1.26)
其中N是晶胞数目。
第三,要求手征对称性必须是强大的,这个要求不是精确陈述的。为了理解这个的含义,首先注意,在固体物理中,我们将此处理具有很多局域参数的哈密顿量,这些参数以一种控制或未控制的方式变化。例如SSH模型,其中跳跃振幅的值可能受到空间无序的影响。我们将所有这些参数放在一个形式矢量中,称其![]() 。这里
。这里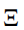 是一组所有无序的实现。 我们应该讨论一组哈密顿量
是一组所有无序的实现。 我们应该讨论一组哈密顿量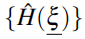 (对所有
(对所有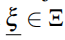 )的对称性而不是一个哈密顿量H的对称性。只要满足以下条件(1.27),则这一组(即
)的对称性而不是一个哈密顿量H的对称性。只要满足以下条件(1.27),则这一组(即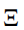 )有由Γ^表示的手征对称性。
)有由Γ^表示的手征对称性。
![]() (1.27)
(1.27)
其中对称算符Γ^独立于参数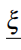 。这就是手征对称性的强大。
。这就是手征对称性的强大。
对各个参数,(1.27)都成立,这就是手征对称性的强大。
1.4.1 手征对称性对能量本征态的影响
由于定义(1.23)中的负号,所以此手征对称性的影响非常不同于传统的对称性的影响。
子晶格对称性
手征对称性也称子晶格对称性。给出了手征对称性算符Γ^之后,我们能定义正交子晶格投影:
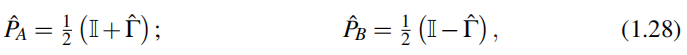
其中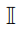 代表系统希空间中的单位元。由(1.28)得
代表系统希空间中的单位元。由(1.28)得![]() 及Γ^=P^A−P^B。
及Γ^=P^A−P^B。
子晶格对称性的定义(1.23)能写成以下等价的形式通过要求哈密顿量不会导致从一个子晶格的某一格点到相同子晶格的某一格点的转变(跳跃),(?不懂)

实际上,可以等价地通过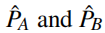 来定义手征对称性。
来定义手征对称性。
对称谱
定义:态![]() 的手征对称partner为
的手征对称partner为![]() 。
。
手征对称的哈密顿量的能谱是对称的。对于任何具有能量E的态,存在具有能量-E的手征对称partner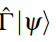 。
。
 (1.30)
(1.30)
(1.29)证明过程中有
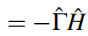
由以上可以知道,有手征对称性的体系,能带是上下对称的。
a.若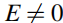 ,
,
则![]() 是具有不同能量本征值的本征态,故它们必须相互正交。 This implies that every nonzero energy eigenstate of H has equal support on both sublattices,(这意味着H的每个非零本征态对两个子晶格都有同等的支持)(?不懂)
是具有不同能量本征值的本征态,故它们必须相互正交。 This implies that every nonzero energy eigenstate of H has equal support on both sublattices,(这意味着H的每个非零本征态对两个子晶格都有同等的支持)(?不懂)
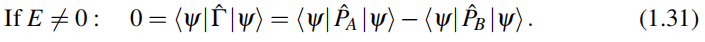
b.若E=0,
则零能本征态可以选择只在一个子晶格上有支持,(?不懂)
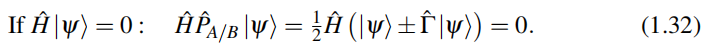
由(1.32)知,零能本征态可以选择为投影的零能本征态![]() ,其中
,其中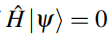 (即
(即 是零能本征态)。
是零能本征态)。
(1.29)证明过程中有
,由此可以证明(1.32)
这些投影的零能本征态![]() 也是Γ^的本征态,且
也是Γ^的本征态,且 ,
, 。
。
1.4.2 SSH模型的子晶格投影和手征对称性
The Hamiltonian of the SSH model, Eq (1.1)
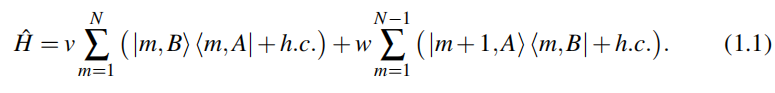
, is bipartite(两分的,两边的):the Hamiltonian includes no transitions between sites with the same sublattice index(此哈密顿量不会导致具有相同子晶格指标的格点之间的跳跃(因为只有最近邻跳跃)). The projectors to the sublattices read
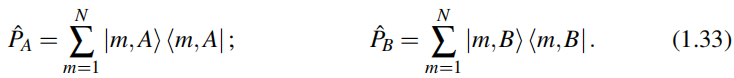
手征对称性由子晶格算符Σ^z表示,由(1.28)知,
(1.33)、(1.34)应该是定义出来的
注意此子晶格算符有手征对称性所要求的所有性质:此子晶格算符是幺正、厄米、局域的。
将(1.33)代入(1.34)即可以证明这些性质
SSH模型的手征对称性重申了哈密顿量是二分的这个事实,
 (1.35)
(1.35)

还可以证明(1.35)这个关系成立不管跳跃振幅是否依赖于位置,所以由Σ^z表示的手征对称性确实是强大的。
书未证此结论
1.4.3 手征对称性的影响:SSH模型的体缠绕数

由于手征对称性,![]() 被限制到位于
被限制到位于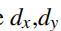 平面,
平面,
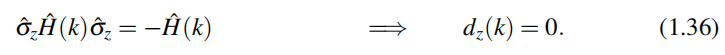

所以我觉得前面1.4.2节不应该用(1.1)哈密顿量,可能应该用第一部分中的(1.7)式体哈密顿量。
由(1.36),则d(k)的端点就是平面上的一个有向闭合环,因此关于原点有一个明确的整数的缠绕数。
缠绕数是重解(重根)的个数
一个从图中获得缠绕数的简单方法是数出d(k)与从原点到无穷远处的曲线的相交的次数。
1)由于d(k)的端点画出的是有向曲线,所以它有左边和右边。左边画为蓝色,右边画为红色,正如显示在fig1.5a中。
2)让有向曲线L从0到无穷。其实它不必一定是直线。一个简单的选择是半无限的线,![]() 。还有两个选择显示在图1.5a中。
。还有两个选择显示在图1.5a中。
3)找到d(k)与L的交点
4)每个交点有一个特征数:如果L从蓝色边遇到这个交点,则为+1,如果L从红色边遇到这个交点,则为-1.
5)缠绕数v等于特征数之和

Figure 1.5:(a) Endpoints端点 of the vector d(k) forming a loop, as k is swept through the Brillouin zone. Blue/red denotes the left/right side of the loop.(b) The loop(gray)is projected to the unit circle(dashed虚线). This projection (red) allows for the compact formula(1.38) expressing the winding number of the loop around the origin. We should display a few arrows showing the direction of the directed curves, both on (a) and(b).
现在我们考虑上面所定义的缠绕数v在L或d(k)的连续变形下如何变化。我们仅允许保持曲线在平面上的变形和保持L从原点到无穷的变形,并且不会产生d(k)=0的点。由于变形,L和d(k)的交点可以移动,但不会改变v。这些交点只能成对地出现或消失,即红色和蓝色的交点一起出现或消失,这样不会改变缠绕数v。例如,图1.5a中,L有两种选择,对应1和3个交点,但这两种选择对应的缠绕数都为+1.
图1.5a中,其实这相当于将一种选择的L旋转到另一种选择的L
缠绕数是一个积分
定义单位矢量:

由于![]() 故对所有的k,(1.37)对
故对所有的k,(1.37)对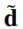 的定义都是良好的。
的定义都是良好的。
映射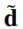 的图像是fig1.5b中的红色圈(电脑才是彩色,或手机):它是d(k)曲线(灰色圈)到单位圆(虚线)的投影。
的图像是fig1.5b中的红色圈(电脑才是彩色,或手机):它是d(k)曲线(灰色圈)到单位圆(虚线)的投影。
我们可以很容易地检验缠绕数v为:
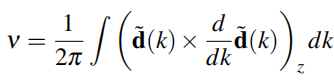 (1.38)
(1.38)
(1.38)的证明(此证明来自前辈@去那遥远的地方):从此证明才可以理解缠绕数的真正含义:

(1.38)的另一形式:
另一种计算缠绕数的方法:从体内部空间哈密顿量来得到:

可以很容易地检验,缠绕数为:
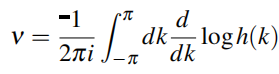 (1.40)
(1.40)
Here during the calculation of the integral, the branch cut for the logarithm is always shifted so that the derivative is always well defined.(?不懂这句话)



understanding basic concept论文中还有一种通过贝里矢势计算缠绕数的公式:
别人的补充,不知是否正确:
关于winding number ,补充几点:

有人补充说,缠绕数是定义在一维,陈数定义在二维。不知道这句话是否对
注意,1.6节总结中说:缠绕数是对平移不变bulk的情况来定义的(这是对非平移不变的情况的替代的定义)
SSH模型的缠绕数
对SSH模型,缠绕数是0或1,这取决于参数。
若胞内跳跃大于胞间跳跃,即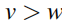 ,则是平庸情况,缠绕数为0.
,则是平庸情况,缠绕数为0.
若胞间跳跃大于胞内跳跃,即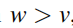 ,则是拓扑情况,缠绕数为1.
,则是拓扑情况,缠绕数为1.
证明:在平庸情况,由于在dx−dy平面,SSH模型中的v是圆心,w是半径,所以v>w时圆没有包括原点,故缠绕数为0.而在拓扑情况,则同理得缠绕数为1.
改变SSH模型缠绕数的方法有两种:如图1.6
(a)推动d(k)的路径通过dx−dy平面的原点
(b)将其提高到平面外,然后在放回到平面的一个不同位置
方法(a)要求关闭体能隙,方法(b)要求破坏手征对称性。
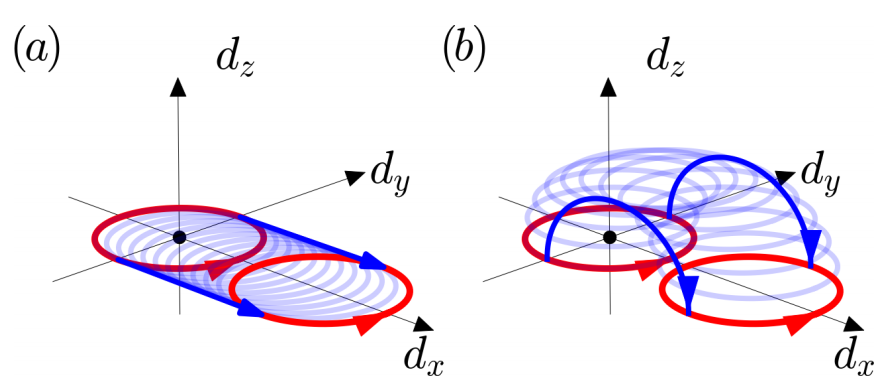
图1.6:: The endpoints端点 of the vector d(k) as k goes across the Brillouin zone (red or blue closed circles), for various parameter settings in the SSH model.
在(a)中,胞间跳跃保持常数w=1,(即圆的半径保持常数),而胞内跳跃v从0增加到2.3. (即圆心从0变到2.3),在这个过程中,体能隙先关闭后再打开,(因为v=w时体能隙才会关闭(如fig1.2,是在一些k,bulk能隙关闭),也就是当圆圈的左边正好在原点时体能隙关闭),缠绕数从1变到0.
在(b)中,胞间跳跃保持常数w=1,而胞内跳跃v从0增加到2.3, 但通过引入子晶格势 来避免关闭体能隙。为了避免关闭体能隙,我们调节参数θ从0到π,并设置
来避免关闭体能隙。为了避免关闭体能隙,我们调节参数θ从0到π,并设置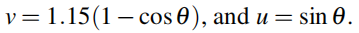 在θ=π时,u=0,没有子晶格势,所以手征对称性恢复。缠绕数从1变成0.
在θ=π时,u=0,没有子晶格势,所以手征对称性恢复。缠绕数从1变成0.
我未证明这种方法可以避免关闭体能隙,没时间
1.5节 边界态的数目是拓扑不变量
绝缘哈密顿量的绝热变形
定义:如果满足以下三个条件,则绝缘哈密顿量是绝热变形:
- 其参数是连续地改变
- 系统的重要对称性仍然保持
- 在E=0附近的体能隙保持打开
绝热变形是假想的过程,实际不会存在。但是如果我们确实将其认为是实际中的过程,绝热定理[1]告诉我们,从多体基态(其与激发态通过一个能隙区分开来)开始,进行足够缓慢的变形,则对于系统的bulk部分来说,最后仍处于基态;但是系统的边界会发生改变。需要说明的是,绝热变形是慢的,但又不是太慢,因此边界仍然应该与bulk区分出来考虑。我们将在第4章回到这一点。
哈密顿量的绝热等价
如果有一个绝热变形将两个绝热哈密顿量连接起来,这两个绝热哈密顿量就被称为绝热等价或绝热连接,这respect(考虑)了重要对称性。例如,SSH模型的相图1.7中,对应于拓扑相(w > v)的两个黑点的两个哈密顿量是绝热连接的,因为可以在它们之间画一条不穿过无能隙拓扑-平庸相边界w = v的路径。
例子中的过程满足绝热变形定义中的三个条件,所以是绝热等价的

图1.7 SSH模型的相图。左上方缠绕数为1,右下方缠绕数为0,通过这种缠绕数的区别定义了拓扑相和平庸相。两个相的分界线v=w,此时体能隙在一些k闭合。在相同的相中的两个哈密顿量是绝热等价的。
拓扑不变量
如果一个描述绝缘哈密顿量的整数在绝热变形下不会改变,则称此整数为拓扑不变量或绝热不变量。
注意绝热变形意味着拓扑不变量的两个性质:
(1)它只在热力学极限中很好地定义。
(2)它依赖于需要被考虑的对称性。
拓扑不变量的一个例子:SSH模型的缠绕数。
热力学极限:在保持n=N/V不变的情况下,使得粒子数N、体积V趋于无穷。为什么拓扑不变量需要定义在热力学极限?不知道
如果两个绝缘哈密顿量的拓扑不变量不同,则它们不是绝热等价的。
证明:因为拓扑不变量不同,所以有拓扑不变量的定义知,这两个哈密顿量不可能通过绝热变形连接起来(因为如果能通过绝热变形连接,则拓扑不变量应相同),所以由绝热等价的定义知,这两个哈密顿量不是绝热等价的。得证。
考虑一个例子,fig1.7SSH模型中分别位于拓扑相和平庸相的两个哈密顿量,它们拓扑不变量不同,所以它们不是绝热等价的;从绝热等价的定义来看,它们不能通过绝热变形联系起来,所以确实不是绝热等价的(注意绝热变形的定义中能隙保持打开);但有人可能认为,在保持手征对称性的同时,通过增加额外的项,连续地改变bulk哈密顿量,这样能连接这两个哈密顿量,这样这两个哈密顿量是绝热等价的。但是毕竟这两个哈密顿量的缠绕数不同,而由“拓扑不变量的定义”知,在绝热变形下缠绕数不会改变,所以上面这个增加额外项连接这两个哈密顿量的过程不可能是绝热变形。故,总之,这两个哈密顿量不是绝热等价的。
边界态的数目是拓扑不变量
从1.3.2节我们已经看到,在SSH模型一端的边界态的数目是一个整数,而且此整数在特定类型的绝热变形下不会改变。我们现在一般化这个例子。
1.3.2节并没有说上面这个结论
考虑在热力学极限,在有能隙手征对称的一维哈密顿量的左端的能量本征态(即 with length N → ∞, in an energy window from -ε < E < ε, with ε in the bulk gap)。在这个能量窗口中可以有非零能量的边界态,也可以有零能量的边界态。每个非零能量态必须有一个手征对称partner,这个态和它的手征对称partner占据相同的晶胞(手征对称算符是局域、幺正的)。零能态的数目是有限的(由于bulk中的能隙),它们中的每个都能被限制到一个单个子晶格。有NA个零能态在子晶格A,NB个零能态在子晶格B。
以上结论不知道为什么
考虑以连续参数d: 0→1为指标的哈密顿量的绝热变形对NA−NB的影响。哈密顿量respect(保持)了手征对称性,它的体能隙超过2ε,对于所有d的值来说。
此变形能产生零能态,通过将一个非零边界态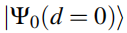 变成零能,
变成零能,
在这种情况,

因此,NA−NB的值不变。
此变形也能将零能态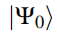 变成能量E>0,在一些
变成能量E>0,在一些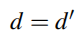 。
。
此变形能将非零态移动进或出 -ε < E < ε 能量窗口。这明显地对NA−NB的值没有影响。
由于此变形,零能本征态的波函数会发生变化,从而使其在bulk中越来越深地扩展。然而,由于绝热变形定义中的有能隙这个条件,零能态必须具有以指数方式向bulk衰减的波函数,因此这个过程不能将它们从边界移开。所以NA和NB不能以这种方式被改变。
上面的论点显示了在左边边界,在子晶格A上的边界态的净数目NA−NB是拓扑不变的。(?为什么是子晶格A,书中这个结论是否有问题)
以上对结论的证明没写清楚,没有用数学证明,我觉得其实说清楚的话应该非常复杂
SSH模型中的体-边界对应
我们已经对SSH模型引入了两个拓扑不变量:缠绕数(1.38)、净边界态数NA−NB。缠绕数仅仅从体哈密顿量得到,净边界态数通过看左边边界的低能部分得到。在SSH模型的平庸情况,v>w,两个拓扑不变量都是0;在拓扑情况,v<w,两个拓扑不变量都是1.
怎么证明净边界态数在两种情况中的值?
这显示了我们能使用体拓扑不变量(缠绕数)去预测在边界的低能物理。这是体-边界对应的一个简单例子。在后面的章节中,体-边界对应将经常出现。
1.5.1 畴壁上的束缚态
边界态不仅出现在开链的两端,也会出现在相同链的不同绝缘区域(绝缘畴)之间的畴壁上。这能通过完全二聚化极限来理解。在fig1.8中的例子有两种类型的畴壁:一种包含单个孤立格点,它有一个零能态(无格点上的势能,所以是零能态);另一种包含一个三聚体。在三聚体中,两个端点的奇叠加组成了零能本征态。在图1.8的例子中,此零能本征态为:

书1.3.1.1节说了奇叠加的含义是这两个态的中间是负号,例如(1.41)
注意,就像链末端的边界态一样(如图fig1.4),畴壁上的这些零能态是只在一个子晶格上具有非零值的波函数。
从一个没有畴的完美的二聚化相,它只可能germinate(产生,萌生)偶数个畴壁。这意味着如果遇到一个”具有在一个子晶格上的局域态“的畴壁,则在系统的某处会有另一个畴壁——可能是在系统的边界有这另一个畴壁,它具有在与前面子晶格不同的另一个子晶格上的局域态。

图1.8:一条长、完全二聚化的SSH链,有3个畴。畴之间的边界,即“畴壁”,拥有零能本征态(黄色阴影)。这些可以局域在单个格点上,例如在m = 3处的畴壁,或者局域在格点的叠加上,例如在m = 6和m = 7晶胞之间共享的三聚体的端点的奇叠加。
考虑不是完全二聚化极限的SSH系统中的一个畴壁。在畴壁上的边界态的波函数将以某个小的深度渗透到bulk中,末尾呈指数衰减。对于两者之间距离为M个晶胞的两个畴壁,在这两个畴壁上的两个边界态将杂化,形成”成键“和“反键”态。在半满情况,只有负能本征态被占据。这个态拥有单个电子,然而,它的波函数是局域的,且波函数在两个畴壁上有相等的权重。因此,每个畴壁,当与其他畴壁、链的末端很好地分开时,将携带半个电子电荷的电荷量。此效应有时称为电荷的“分数化”。
1.5.1这节没有数学证明
1.5.2 边界态的精确计算
即使在不存在平移不变性的情况下(即不考虑周期性边界条件),也可以精确地计算出SSH模型的零能边界态。考虑具有N个晶胞的SSH模型,它具有复数的胞内、胞间跳跃振幅,
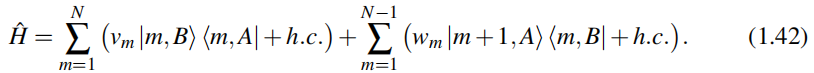
(1.42)不是bulk哈密顿量
(1.42)是(1.1),是没有考虑周期性边界条件的哈密顿量,它不是bulk哈密顿量
寻找此哈密顿量的一个零能本征态,
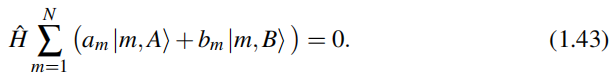
这给了我们2N个线性齐次方程,关于2N个振幅am和bm,
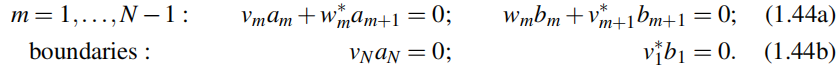

(1.44a)是对都成立。
(1.44a)由累乘法得:

而由(1.44b)得:

由(1.45)、(1.46)、(1.47)得:
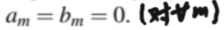
即此哈密顿量的零能本征态不存在。
虽然没有零能本征态,但是在热力学极限N → ∞下,如果平均胞间跳跃比平均胞内跳跃更强(其实准确来说应该是(1.48)中的![]() >
>![]() ),则该问题存在两个近似解。证明:
),则该问题存在两个近似解。证明:
先定义“bulk平均值”:
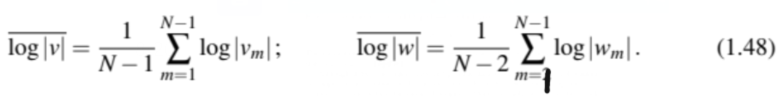
为什么这样定义以及整个过程的解释见后面
对(1.45),令m=N;对(1.46),令m=1,得:
 (1.49)
(1.49)
其中局域长度:

我认为称为近似解的原因是,注意到此时(1.49)在热力学极限下与(1.47)近似等价,所以这种解称为近似解。
如果在热力学极限下,bulk平均值(1.48)有意义,且ξ>0,则我们有两个近似零能解,
 (1.51)
(1.51)

其中am,bm由(1.45)、(1.46)得到,而只有得到a1和bN才能由(1.45)、(1.46)得到am,bm;a1和bN分别用来确定![]() 和
和![]() 的模。
的模。
(其实我认为a1和bN可以人为任意选取,因为a1和bN任意选取都可以使得(1.47)近似成立、(1.45)、(1.46)成立;即a1和bN任意选取都可以使得![]() 是近似零能解。不过数值计算中可能是取使得(1.47)近似成立比较好的a1和bN。)
是近似零能解。不过数值计算中可能是取使得(1.47)近似成立比较好的a1和bN。)
a.因为其近似满足(1.45)、(1.46)、(1.47),所以它是近似为零能的解。但这样说不严谨,怎么严谨证明它是近似为零能的解,可能要通过解薛定谔方程来证明,没时间。
b,ξ>0这个条件是使得(1.49)近似符合(1.47)。热力学极限是因为(1.49)证明过程中用到了热力学极限这个条件。
c.重要问题:为什么选取(1.51)这种分别去掉了bm和am项的形式?其他的近似零能解的形式会考虑吗?
原因:


边界态的杂化

注意(1.53)、(1.54)说明杂化态的能量随系统尺寸是指数小的,系统尺寸指的是晶胞数目N。注意理解上面这句话的意思是说,系统尺寸(晶胞数目N)越大,杂化态的能量越小。
边界态的杂化这部分书中没说清楚
1.6节 总结
一维手征对称的晶格绝缘体的两端可以有拓扑保护的零能边界态,这可以由bulk的缠绕数来预测。
手征对称的晶格绝缘体:
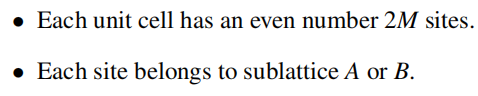

最后这个不懂
边界态:
- 波函数局域在边界,向bulk中指数衰减
波函数指数衰减这个未证明,书中没写
- 波函数仅支持一个子晶格(两个边界分别有两个不同的子晶格)
- 能量在系统随系统尺寸(晶胞数目N)是指数小的,
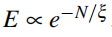 。
。
缠绕数:
- 缠绕数是对平移不变bulk的情况来定义的(这是对非平移不变的情况的替代的定义)
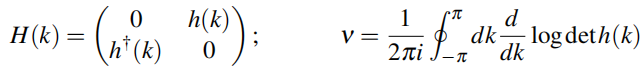 (1.55)
(1.55)
最简单的例子是SSH模型,
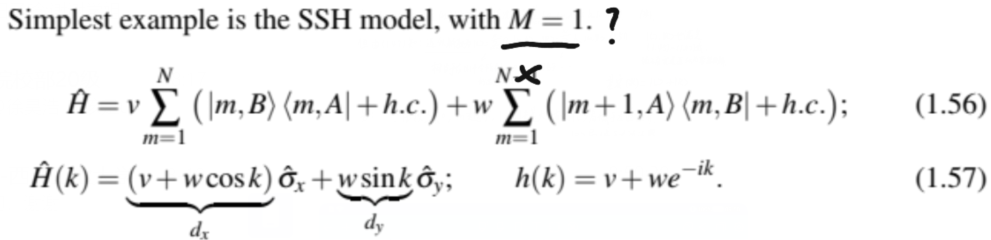
- 若v>w,平庸
- 若v<w,拓扑

- 这种情况的缠绕数:
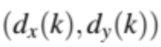 端点的缠绕。
端点的缠绕。
重要:体-边界对应:我们能使用体拓扑不变量(缠绕数)去预测在边界的低能物理
附件列表