##nolting多体物理第二章多体模型系统2 晶格振动

2.2节晶格振动
1.简谐近似
1）离子子系统的动能、势能
2）原子力常数矩阵
3）位移u的方程（2.127）
4）极化矢量

ε_{s}^{(r)} (q)

、位移u的方程（2.127）的通解（2.142）、色散关系、简正坐标（2.143）
2.声子气
1）离子子系统哈密顿量（2.152）
2）简正模（每个简正坐标对应一个振动模式，即简正模）。一个简正模的能量（即一个振动模式的能量）、系统能级的表达式
任一原子的通解是这3nN个特解的叠加！
3）量子化
4）量子化后，哈密顿量的表达式：
5）简正坐标随时间变化公式、产生湮灭算符随时间变化公式
6）声子、声子气体(即无相互作用的声子组成的气体）
3.李正中书的内容：
4.callaway书的内容：
注意归一化的n声子态的公式：

量子化得到声子的过程有两种，一种是callaway书中的量子化的过程及公式，一种是nolting书、李正中书的过程及公式.
我觉得很奇怪，nolting是一个写书很严谨的人，为什么我不能从书中说的“从（2.157）证（2.166）”？也许nolting书错了？不知道
nolting书这一节的公式其实和李正中书的公式完全一样，以后学李正中书！
nolting书这一节和M. T. Dove,Introduction to lattice dynamics书第4、6章讲晶格振动很类似。Dove书写得更多内容，写得好，但可能没时间。而callaway书中文版写得也和nolting书这里完全类似，写得好，晶格振动以后一定学callaway书，这本才是固体理论书。

此固体理论讲义写的晶格振动、声子也参考了callaway的书，好像也很好。

2.2节晶格振动

在第2.1节中，假设晶格离子是静止的，只研究了电子系统的激发。按照(2.6)中的程序，我们现在要更详细地讨论离子子系统；即(2.3)的哈密顿量现在将是关注的中心。

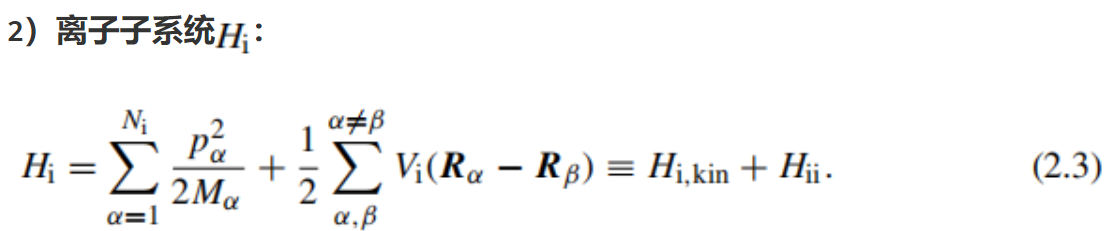
如果能量被转移到单个晶格离子，例如通过粒子碰撞，由于强烈的离子-离子相互作用，它将迅速分布在整个晶格上。局域激发将转变为集体激发，最终所有晶格格点都参与其中。因此，在数学描述中使用仍待定义的集体坐标来代替离子坐标是有利的。在这个表象中，晶格振动可以被量子化。相应的量子称为声子。

1.简谐近似

1）离子子系统的动能、势能

晶格振动所需的恢复力( restoring forces)是结合力(bonding forces)，它可以有相当不同的物理来源。然而，定性地说，对势（pair potential） $V_{i} (∣ R_{α} - R_{β} ∣)$ 总是具有相同的形式。势能最小值定义了平衡距离 $R_{α β}^{(0)}$ 。所谓的简谐近似包括将势能曲线的末端近似视为抛物线，这对于偏离平衡距离较小的偏移量似乎是合理的。接下来我们将更定量地讨论这一点。
我们的起点将是一个【基矢包含p个原子】的Bravais格子（即复式格子），正如我们在(2.9)中描述它：

其中 $s = 1, 2, \dots, p$ and $m \equiv (m_{1}, m_{2}, m_{3}); m_{i} \in Z,$

（其中的 $R_{α}^{(0)}$ 是离子平衡位置）

根据此注释中（2.9）知道，（2.118）中的 $R_{s}^{m}$ 其实是离子平衡位置。
令：
$x_{s}^{m} (t)$ ：是第 $(m ， s)$ 个原子的瞬时位置，
$u_{s}^{m} (t)$ ：是第 $(m ， s)$ 个原子偏离平衡的位移。
结果我们发现：

晶格离子的动能由下式给出：

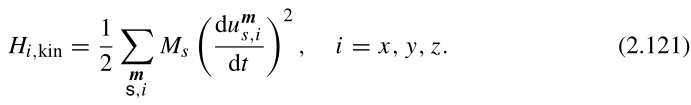
根据动能表达式 $E = \frac{1}{2} m v^{2}$ 知道此式确实成立。

对于势能，我们写道：

其中，
表示所谓的结合能(binding energy).

结合能 $V_{0}$ ：是离子处于平衡位置时的势能。
离子-离子之间的势能是指库伦相互作用的势能+泡利原理产生的排斥势，其中电势能的表达式见固体物理笔记本”离子晶体“一节，见北大固体物理65页（3.0.1）：
（此哈密顿量少了泡利原理产生的排斥势等）
固体物理笔记本：

对非极性分子晶体，还有非极性分子间的瞬时电偶极矩相互作用（范德瓦尔斯相互作用等），见固体物理笔记本。

我们在平衡位置附近展开V(图2.4)：

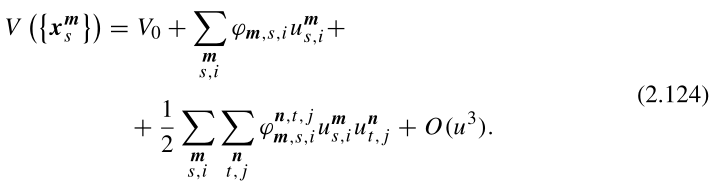
因为势能V与所有原子都有关（因为对势），根据多元函数泰勒展开，就得到(2.124)式。

图2.4 固体中对势(pair potential)的简谐近似图示

此图的原因查课件等，没时间

简谐近似现在包括忽略余数 $O (u^{3})$ 。位移u通常小于晶格间距的5%，因此简谐近似是非常合适的。因此，高阶项，即所谓的非谐项，最初是不感兴趣的。
对于(2.124)中的偏导数 $ϕ$ ，我们发现：

这就是平衡位置的定义。

因为平衡时势能取极小值，故（2.125）成立。类似课件：

2）原子力常数矩阵

二阶导数形成一个原子力常数矩阵

为了更好地理解这一重要矩阵，以下陈述非常有用：
$- φ_{m, s, i}^{n, t, j} u_{t, j}^{n}$ ：是 $i$ 方向的力，它是【在当第 $(n ， t)$ 个原子在 $j$ 这个方向上移动了 $u_{t, j}^{n}$ 位移，而所有其他原子保持不变时】，作用在第 $(m ， s)$ 个原子的力。

此陈述的原因：M. T. Dove,Introduction to lattice dynamics书83、84页(这两页看起来有些东西没解释，其实是因为在前面章节解释过了，所以应从前面一些章节开始学）等，介绍了原子力常数和（2.127）式等，适合初学者，有时间才学：

原子力常数这些内容在三维晶格振动的内容中有，故可能在黄昆晶格动力学（有中文版）等书也可能有.
我自己对此陈述的一个理解：

3）位移u的方程（2.127）

因此，简谐近似对应于线性作用力定律，如在谐振子中：

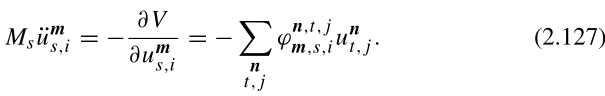
根据牛顿定理f=ma和上面的陈述知此式成立。李正中书说此式也可以由哈密顿量正则方程得到，证明见李正中书。

力常数矩阵有几个明显的对称性。它直接根据其定义（2.126）得出以下结论：

平移整个固体 $Δ x = (Δ x_{1}, Δ x_{2}, Δ x_{3})$ ，力自然保持不变。因此，它是从

得到以下公式成立：

最后，平移对称性得到：

（2.129）、（2.130）证明：

4）极化矢量 $ε_{s}^{(r)} (q)$ 、位移u的方程（2.127）的通解（2.142）、色散关系、简正坐标（2.143）

为了解(2.127)，我们首先采用以下形式的试解：

代入(2.127)，得到本征值方程：

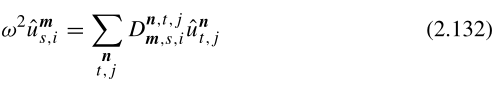
其中实对称矩阵：

（2.132）、（2.133）证明:

它（指的是（2.133））有3pN个实本征值 ${(ω_{s, i}^{m})}^{2}$ ，因此本征值 $ω_{s, i}^{m}$ 同样是实数或纯虚数。只有实本征值才代表物理解。利用平移对称性(2.130)，特征值问题的维数从3pN降低到3p：

这里，我们使用了以下定义：

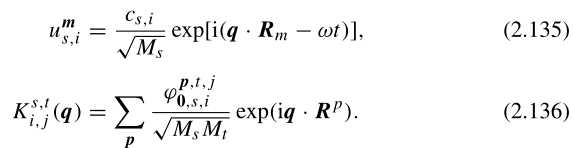
设为（2.135）形式的原因见Dove书第六章（6.18）和第四章也有写原因等，有写，但我没时间读。其实原因应该见李正中书

等式(2.134)是具有3p个特征值的矩阵K的特征值方程，这3p个本征值为：

晶体是各向异性的。因此，对于每个方向 $q / | q |$ ，必须将这些色散分支 $ω_{r} (q)$ 确定为 $q = | q |$ 的函数。有关双原子线性链的标准例子的详细信息，可以在固体物理教科书文献中找到。我们可以在那里找到(习题2.2.1)：
$\begin{aligned} 3 支声学支 & ⟺ ω (q = 0) = 0 \\ 3 (p - 1) 支光学支 & ⟺ ω (q = 0) \neq 0 . \end{aligned}$

固体物理笔记本中写了，3p支中有3支声学支，3(p-1)支光学支。一维双原子链的色散关系见笔记本图，即知道上面的结论。

由于周期边界条件，波数 $q$ 是离散的。如果 $G$ 是倒易格子中的任意向量，则由于 $\exp (i G \cdot R^{m}) = 1$ ，我们有：

这意味着人们只需要考虑第一布里渊区内的波数 $q$ 。运动方程的时间反转不变性最终导致：

（2.138）证明：

（2.139）证明：我之前写的一个（2.139）的证明（此证明错误）:

K矩阵不变，则根据久期行列式为0而得到的色散关系不变，故得：，因为频率取正实数，故（2.139）得证。
但是后来我发现上面这个证明错误，因为上面证明过程中这句话错误，因为

故上面这个证明错误。
正确证明是根据callaway书中的证明来证：
callway书第4页：

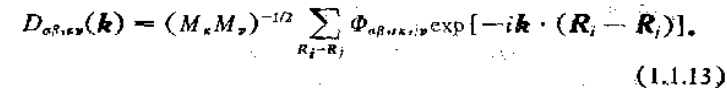
(此证明中有一些过程省略了，比如其实需要证明K矩阵（类似callaway书中的D矩阵）是厄米矩阵，可能可以通过石墨烯格子特殊值法来证，比较复杂，我未证明，还有一些证明过程，没时间省略。）
故根据以上callaway书的证明过程，完全类似地就可以得到，因为频率取正实数，故（2.139）得证。

注意完全类似callaway书(1.1.21)的证明过程，可以得到一个较重要的结论:（2.139.1）

对于 $3 p 个 ω_{r}$ 中的每一个 $ω_{r}$ ，方程(2.134)有一个解：

因为i可以取x，y，z，故其实 $ε_{s}^{(r)} (q)$ 是一个矢量，在李正中书中称此为极化矢量 $ε_{s}^{(r)} (q)$ .

（2.140）可以选择为使得正交关系成立：

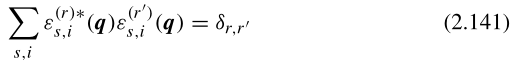
怎么证明存在使得正交关系成立的解？没时间。callway书说了这个完备性和正交性条件可以得到，但没写出过程。应该见李正中书
callaway书：

因此，运动方程(2.127)的通解最终被发现为：
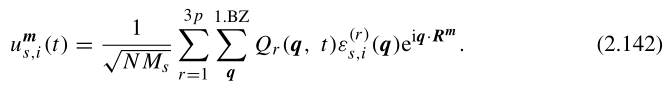（任一原子的通解是这3pN个特解的叠加，见证明过程）
这里，我们将时间因子 $\exp (- i ω_{r} (q) t)$ 包括在叠加系数 $Q_{r} (q, t)$ 中。
使用求出简正坐标 $Q_{r} (q, t)$ ：

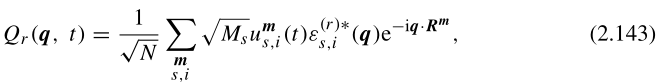
其遵守谐振子运动方程：

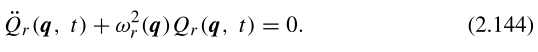
（2.142）、（2.143）、（2.144）证明：
根据课件中：任一原子的通解是这3pN个特解的叠加

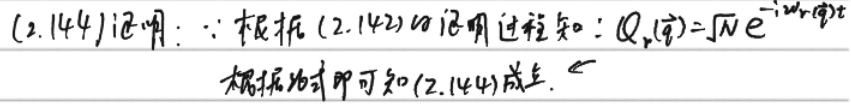
后来我发现上面这些证明过程中写的错误，因为通解是特解的线性叠加，还有叠加系数，我漏了叠加系数，加上叠加系数就应该是：。（为什么叠加系数没有含t？我觉得可能是一种假设，为了符合实验，或者有其他原因，没时间，算了）
（2.144)还可以用哈密顿量正则方程来证明，见李正中书。

注意，实际上（2.142）证明过程中得到的简正坐标表达式：（2.165）很重要。

2.声子气

1）离子子系统哈密顿量（2.152）

前面几节的简谐近似给出了离子系统的拉格朗日函数L=T−V的以下表达式：

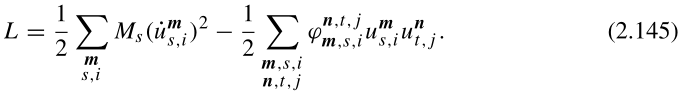
根据（2.124）：
，若忽略结合能，则得到（2.145）。

我们希望用简正坐标表示L。我们重新安排，利用：

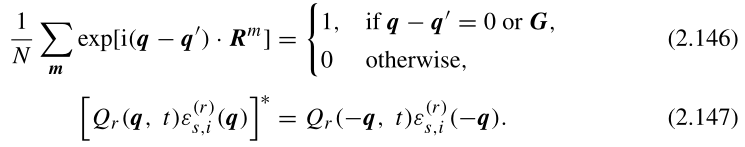
(2.147)证明：为使得位移 $u_{s, i}^{m}$ 是实数，根据（2.142）的共轭复数等于其本身可以知道(2.147)式必须成立。
（2.146）证明：在为知傅里叶变换：

动能：

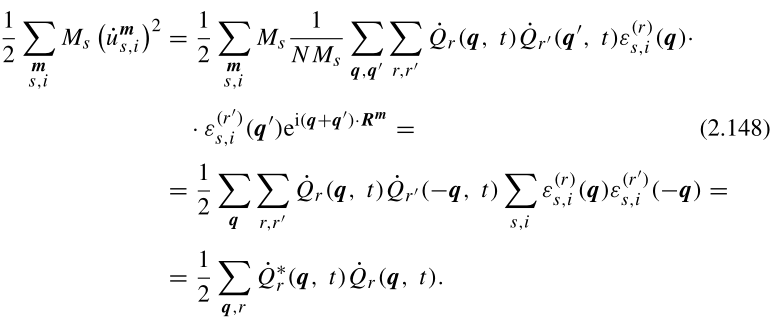
（2.148）证明：
（这里取系数c=1严谨吗，不知道，在callaway书证明(1.1.21)时也用了一个取c=1的方法，我也不知道合理吗，没时间，算了，也许就是为了符合实验？没有为什么？）

以类似的方式，我们找到势能：

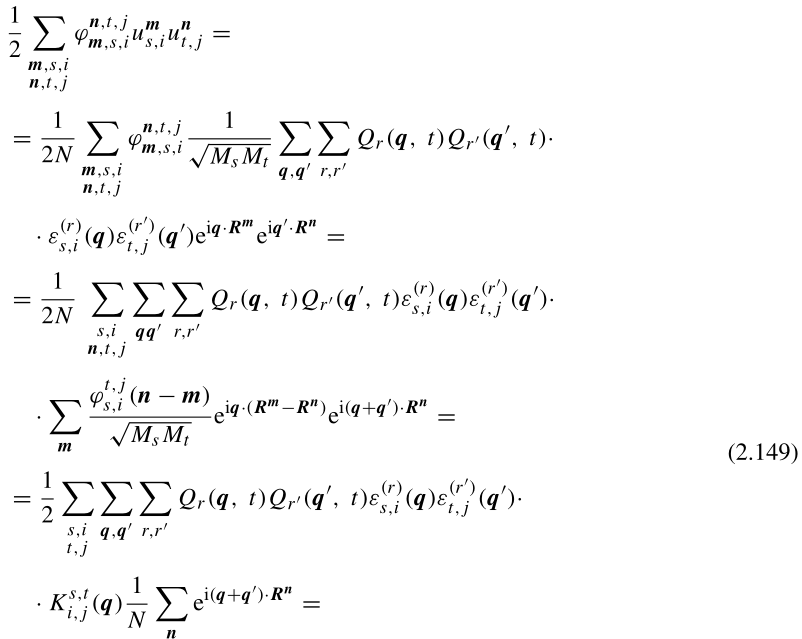
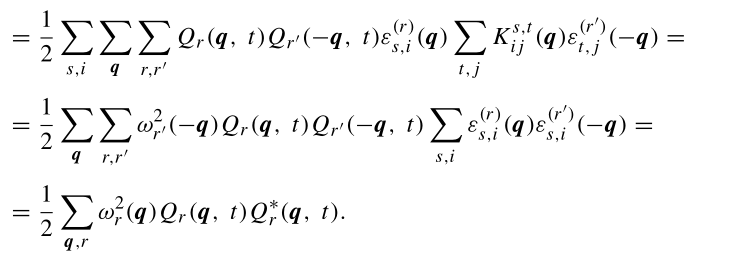
（2.149）证明：没时间，省略，其中倒数第三行到倒数第二行的证明是：

综上，拉氏量：

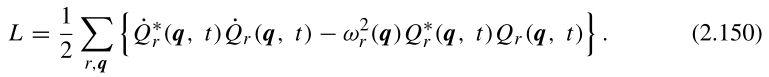
正则动量：

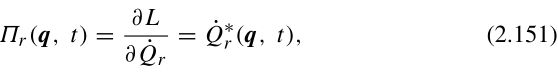
这样算正则动量的原因见为知量子场论笔记。

哈密顿量H=T+V：

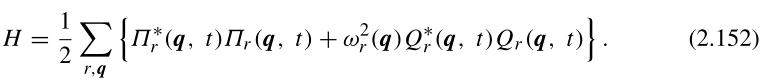
这是一个值得注意的结果，因为通过变换到简正坐标，我们已经证明哈密顿量分解成3pN个非耦合线性谐振子的和。

但是根据李正中书32页，此说法不对。李正中书：

根据李正中书知道，应该是哈密顿量（2.164）才代表3pN个无耦合谐振子：

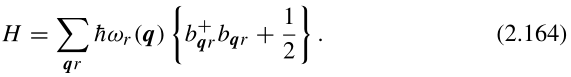
经典谐振子的哈密顿量是 $\frac{1}{2 m} p^{2} + \frac{1}{2} k x^{2}$ .

2）简正模（每个简正坐标对应一个振动模式，即简正模）。一个简正模的能量（即一个振动模式的能量）、系统能级的表达式

固体物理课件中有一些补充内容：每个简正坐标对应一个振动模式，即简正模。一个简正模的能量（即一个振动模式的能量）、系统能级的表达式见课件。
这些课件内容重要，一定应复习：

任一原子的通解是这3nN个特解的叠加！

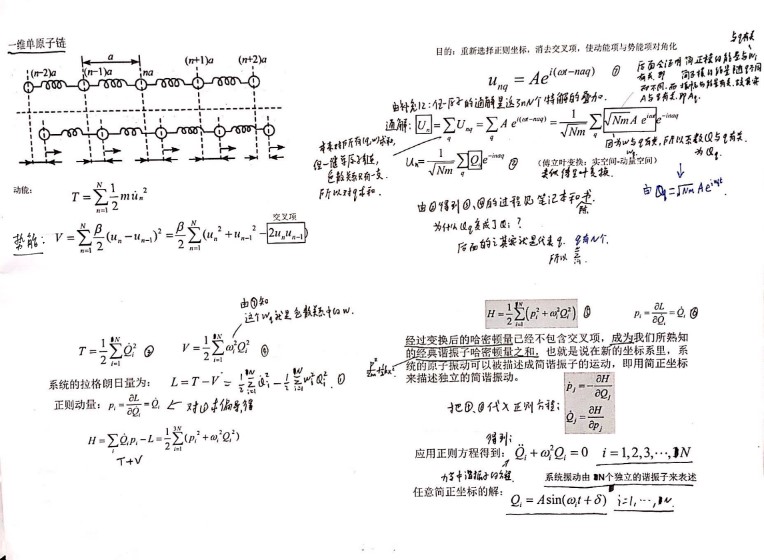
声子：

3）量子化

下一步是对经典变量进行量子化。位移 $u_{s, i}^{m}$ 和动量 $M_{s} {\dot{u}}_{s, i}^{m}$ 现在变成了具有基本对易关系的算符：

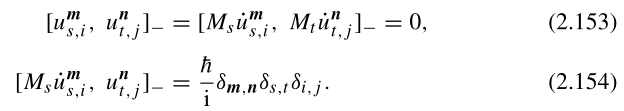
通过代换，我们得到了简正坐标及其正则共轭动量的对易关系：

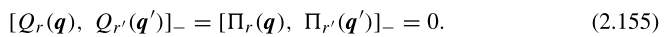
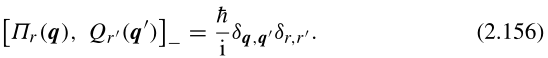
证明：使用(2.143)和(2.153)，我们立即获得：

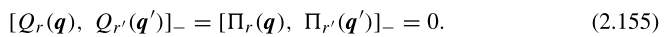
对于第三个关系，我们使用(2.154)从而得到：

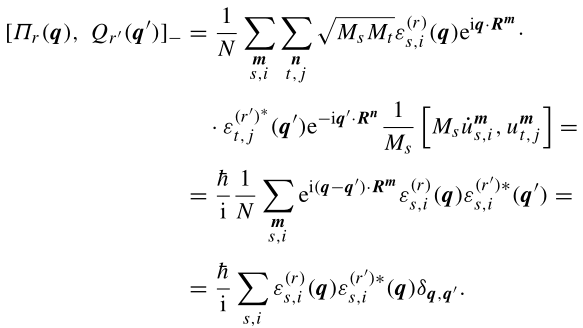
利用(2.141)，最终得出以下结论：

引入产生湮灭算符 $b_{q r}$ 和 $b_{q r}^{+}$ ：

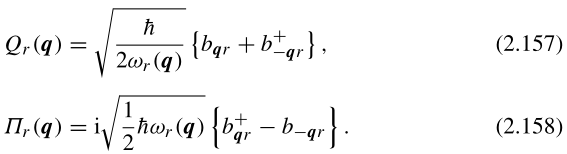
从以上两个公式可以直接得到：
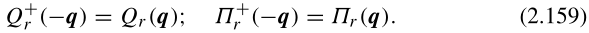（从此式知，简正坐标和其共轭动量不是厄米算符）
及产生湮灭算符：

1.（2.157）、（2.158）这里并不是类似量子化KG场论.md中量子化复KG场时引入两种产生湮灭算符a和b，而是只引入了一个b，可能是因为拉氏量（2.150）和复KG场拉氏量不同。
2.（2.159）的另一种证明方法：这里简正坐标Q和其共轭动量 $Π$ 是复数，故量子化后不需要它们是厄米算符这个条件。在量子力学笔记本中有：实验上对任一被测态可观测的力学量，当然要求平均值是实数，相应的力学量算符要求为厄米算符。故位移算符 $u_{s, i}^{m}$ 是厄米算符。再根据（2.143）：
和（2.139.1）知道：

（2.159）得证。
3.（2.157）、（2.158）这样构造和引入产生湮灭算符的原因：
（2.157）、（2.158）这样构造和引入产生湮灭算符，有 $q$ 和 $- q$ ，好像有点奇怪，但我认为其原因可能就是：前面2.中已经用另一种方法证明了（2.159）： $Q_{r}^{+} (- q) = Q_{r} (q); Π_{r}^{+} (- q) = Π_{r} (q)$ ，此式中就有 $- q$ ，故为了满足（2.159），且完全类比量子力学笔记本中谐振子升降算符解法中：
的系数，并且为了得到只含q的哈密顿量表达式（2.164），就猜测地构造了（2.157）、（2.158）。（在量子化KG场的笔记中也是猜测地构造了场算符用产生湮灭算符来表示的表达式）
4.callaway的书中量子化的过程和这里有点不同，其产生湮灭算符的表达式（1.4.13）和这里的（2.160）（2.161）稍微有些差别在于简正坐标和共轭动量上的共轭符号；但最后得到的哈密顿量表达式都相同，都是（2.146）这个公式。callaway书的内容见后面，其中提到callaway书中得到声子的二次量子化的详细讨论有schweber(1961)给出。
5.李正中书量子化得到声子的公式都和这里的相同

产生湮灭算符的对易关系：

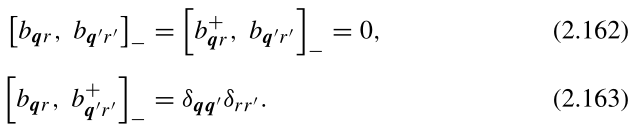
因此它们是玻色子算符。

证明：

4）量子化后，哈密顿量的表达式：

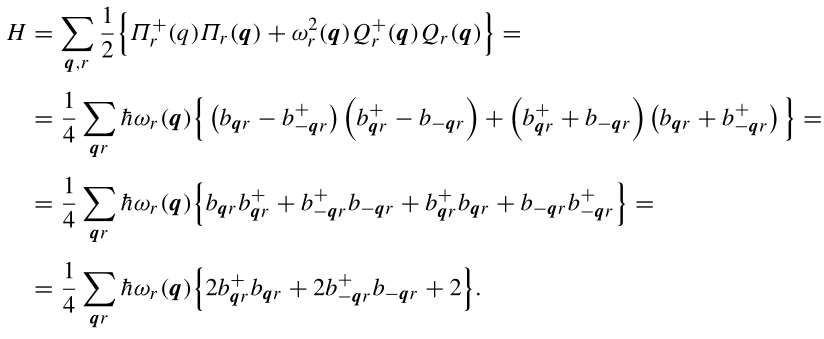
我们还可以利用(2.139)：，然后在简谐近似下获得离子晶格的量子化振动的哈密顿量( Hamiltonian for the quantised vibrations of the ion lattice)：

我们在这里处理的是一个3pN个非耦合谐振子的系统。

5）简正坐标随时间变化公式、产生湮灭算符随时间变化公式

在(2.157)和(2.158)中，我们抑制了简正坐标 $Q_{r}$ 及其正则动量的时间依赖性。如(2.142)所述，它简单地通过以下方式给出：

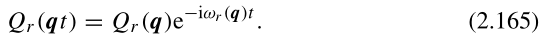
（2.142）相关内容：

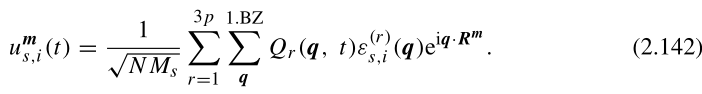
这意味着，根据(2.157)可以知道：

我不知道怎么根据（2.157）证(2.166)，我计算了，发现无论是根据（2.157）还是（2.160），都无法证明（2.166），所以我认为（2.157）（2.158）（2.160）（2.161）这些公式中也许有问题，但或者没有问题，而是可能从一开始的（2.151）式共轭动量：就错误，而callaway书中Q的共轭动量取为（这种取法只是为了符合实验吧，或者有其他原因，callaway书没说）：,此式中并没有复共轭，因为没有复共轭，故就可以根据callaway书中产生湮灭算符表达式（1.4.13）来证明这里的（2.166）.
但是李正中书中对声子的处理和公式和nolting书这里公式都一样，所以nolting书应该也有正确性。
后来我查到了李正中书，在海森堡绘景，算符随时间变化，态不变；注意量子化KG场论.md中海森堡绘景：

故在考虑（2.165）、（2.166）之前，此节的量子化过程是正则量子化（也称等时量子化，在t=0时刻进行量子化）；现在考虑（2.165）、（2.166）就是海森堡绘景。
李正中书：

故（2.166）得证。

我们希望证明这一结果（2.166）与
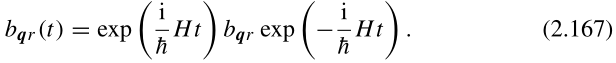一致。

（2.167）证明：法1：其实（2.167）就是海森堡绘景中算符表达式，见金老师高量讲义或量子化KG场中：
故得证。
法2：我们首先证明这一断言：

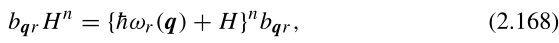
使用完全归纳法：

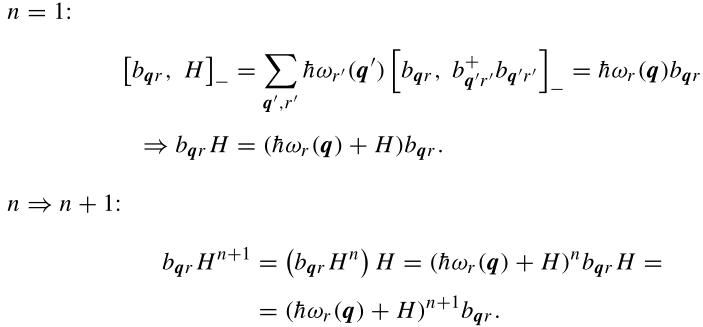
（这里是假设n时（2.168）成立，再推导出n+1的情况）
故（2.168）得证。
故：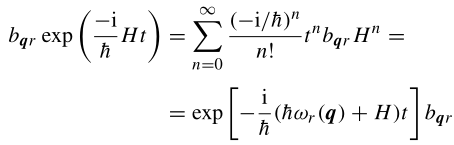
将此式代入（2.167），就得到（2.166），故（2.167）和（2.166）一致。

6）声子、声子气体(即无相互作用的声子组成的气体）

这一部分的基本结果是(2.164)。这清楚地表明晶格振动的能量是量子化的。基本量子 $ℏ ω_{r} (q)$ 被解释为准粒子声子的能量。具体地说，人们会联系推广到以下几个方面：
$b_{q r}^{+}$ ：【一个 $(q, r)$ 声子】的产生算符,
$b_{q r}$ : 一个 $(q, r)$ 声子的湮灭算符,
$ℏ ω_{r} (q)$ : 【一个 $(q, r)$ 声子】的能量.

这些推广的证明过程见* 李正中书33-35页

因为产生湮灭算符满足玻色子对易关系，故声子是玻色子！因此，每个振动状态都可以被任意多个声子占据。

这一节的基础是简谐近似，它将离子晶格建模为无相互作用的声子气体。在位势V的级数展开式(2.124)中被忽略的位移 $u_{s, i}^{m}$ 中为三阶或更高阶的项(这些项是晶格的非谐性)，这些项可以被解释为耦合，即声子之间的相互作用。它们对于描述热膨胀、热平衡的方法、热导率、 $c_{p}, c_{V},$ 的高温行为等效应是很重要的。
简谐近似下，是无相互作用声子气体（玻色子气体，玻色子和玻色子之间无相互作用，此无相互作用玻色子系统（声子气体）中的每个玻色子（声子）的能量为 $ℏ ω_{r} (q)$ ）的原因：

在金老师讲义二次量子化中，对无相互作用玻色子系统，哈密顿量表达式就类似（2.4.22）[（2.4.22）只是多了一个零点能]（注意以上李正中书的几个公式中 $σ$ 不是自旋，而是色散关系的支的指标 $r$ ）
，将此能量表达式对比（2.4.23）知道，无相互作用玻色子系统（声子气体）中的每个玻色子（声子）的能量为 $ℏ ω_{r} (q)$ .