物理学中的群论 第二章 基本概念
第二章 基本概念
1.1节 群及其乘法表
1.对称变换集合的一般性质
1)系统的对称性:指它对某种变换保持不变的性质。
2)对称变换:保持系统不变的变换。(背)
3)变换的乘积法则:相继做两次变换
4)系统的对称变换群
5)例:
2.群的定义
群的例子:
GL(n,C)群:全体 n 维非奇异矩阵的集合。
GL(n,R)群:全体n维非奇异实矩阵的集合。
U(n)群:全体n维幺正矩阵的集合。
O(n)群:全体n维实正交矩阵的集合。
3.群的定义的补充说明
6)乘积的逆:
7)阿贝尔群:元素乘积都可以对易的群
8)有限群:元素数目有限的群
9)有限群的阶:有限群中的元素数目
10)有限群群元素的阶:有限群任一群元素 R 自乘若干次后一定可以得到恒元,满足的最小正整数n称为元素R的阶。(背整个这句话)
11)无限群:元素数目无限的群
12)无限分立群:元素数目可数(即可以数出其中几个)的无限群。
13)连续群:元素可以用一组连续变化的参数来描写的无限群。
4.循环群及其生成元
1)循环群:由一个元素 R 及其幂次构成的有限群,记作。(背)
a.n阶循环群的一般形式:
b.循环群的性质:
c.绕空间固定轴转动角的变换R生成的群
d.n次固有转动轴
5.有限群的生成元和秩
1)元素R 的周期:由有限群的任一元素 R 及其幂次生成的集合。
2)有限群的生成元:有限群的群元素可以由最小数目个群元素的乘积生成,这些最小数目个群元素 (背)
3)有限群的秩:生成元的个数
4)有限群生成元的选择并不唯一,但秩不变。
6.有限群的重排定理
1)复元素:把有限群部分元素的集合看作一个整体
2)重排定理(考试简答题)
7.同构
同构的定义:
8.有限群的乘法表
1)乘法表:
2)乘法表的性质:
3)循环群的乘法表
4)四阶群(即有4个元素的有限群)只有两种:若四阶群中含四阶元素,则为群、若四阶群中不含四阶元素,则为群
群:一个恒元加3个2阶元素。其为:
5)准确到同构,六阶群只有两种:若含六阶元素,则是群、若不含六阶元素,则是群。
群(正三角形对称变换群)
群是最简单的非阿贝尔群。
6)正N边形对称变换群——群
群的乘法表
1.2节 群的各种子集
1.子群
1)定义:群 G 的子集 H,若按照原来的元素乘积规则,也满足群的四个条件,则称为群G的子群。(背)
2)判断有限群的子集是否构成子群,只需检验子集是否满足封闭性即可:
3)任何群都有两个平庸的子群:恒元和整个群。
4)任一元素的周期构成循环子群,与阶数相同的循环群同构。
5)寻找有限群的子群的最好办法:(背)
a.列出全部循环子群
b.把若干个循环子群并起来
c.看它们是否满足封闭性(判断是否满足封闭性:判断其中每一个元素的周期是否都在里面,再判断某两个元素的乘积是否会出去)。恒元、拉定理、封闭性。
6)常见群的子群的例子
2.陪集和不变子群
1) 左陪集 和 右陪集
2)陪集的性质
3)拉格朗日定理:群G的阶数g是其子群H阶数h的整数倍(即子群的阶数是群G的阶数的因子(背,考试简答题)),g=dh,其中d称为子群H的指数。
4)不变子群
5)不变子群的性质
a.阿贝尔群的所有子群都是不变子群(背)。
b.指数为2的子群一定是不变子群(背)。
c.不变子群与类的关系:不变子群必然由若干个完整的类组成 (背)。由若干个完整的类组成的若是一个子群,则必然是不变子群。(这个性质可以用来判断不变子群)
6)商群
7)从乘法表找子群的陪集:
(考试和作业中经常有这个题,随便给一个群进行分析,记住这个例题的过程)求群的所有子群及其陪集,判断不变子群:
3.共轭元素和类
1)共轭
定义:对群G中的两个元素和,如果在群G中存在一个元素S,使得和可以通过联系起来,则称和共轭,记为 (背)
共轭的性质:
2)类
a.定义:所有相互共轭的元素形成的集合,记作
b.类的性质
3)相逆类、自逆类
4)用乘法表判断两元素是否共轭、用乘法表找出类:
5)系统对称变换群群的类
a.等价轴:一般地,若两个同次轴的正方向可以通过对称群中的元素联系起来,则这两个转动轴称为等价轴。(背)
b.双向轴(非极性轴):
c.等价轴、双向轴的性质:
d.举例:D3 群、D4群的类:通过(1)分析轴是几次的、(2)轴是双向轴还是等价轴,(3)再通过等价轴、双向轴的两个性质就能判断类。
6)寻找有限群的类和不变子群的步骤
a.不变子群与类的关系:不变子群必然由若干个完整的类组成 (背)。由若干个完整的类组成的若是一个子群,则必然是不变子群。(这个性质可以用来判断不变子群)
b.寻找有限群的类的步骤:
c.寻找有限群的不变子群的步骤:
7)系统对称变换群群的类和不变子群
1.3节 群的同态关系
1.群的同态:
同态的性质:
2.同态核定理:若G‘与G同态,即G‘~G,则与G‘恒元对应的G中元素的集合H构成群G的不变子群,与G’其它每一个元素相对应的G中元素的集合构成H的陪集,即群G’与群G关于H的商群同构,,H称为同态对应的核。
3.集合G‘与群G的同构或同态
1.4节 正多面体的固有对称变换群
1.固有转动:三维空间中保持坐标原点不变、保持手性不变、保持任意两点间的距离不变的转动称为固有转动。
2.非固有转动:若转动后再做空间反演,则坐标系的手性会发生改变,
3.点群:让体系的一个点保持位置不变的操作构成的变换群。
4.固有点群:由固有转动的集合构成的有限群称为固有点群,包括群、群及正多面体固有对称变换群。
5.非固有点群:由固有转动和非固有转动的集合构成的有限群称为非固有点群。即包含非固有转动的群。
6.正多面体
1)定义:各个面都是全等的正多边形的多面体
2)可能的正多面体及其参数
3)对偶正多面体:将正多面体各个侧面的中心作为顶点联结起来构成的图形也是正多面体,称为原正多面体的对偶正多面体。
a.如果两个正多面体互相对偶,则它们的对称变换群相同。(背)
b.T群、O群、I群
c.正N面体的固有点群的阶数为2L。L:棱数
7.正四面体固有点群—T群
8.立方体和正八面体固有点群—O群
9.正十二 、 二十面体固有点 群—I 群
1.1节 群及其乘法表
1.对称变换集合的一般性质
1)系统的对称性:指它对某种变换保持不变的性质。
保持不变的变换越多,系统对称性越高。
2)对称变换:保持系统不变的变换。(背)
系统的对称性质由对称变换的集合来表示。
3)变换的乘积法则:相继做两次变换
封闭性:两个对称变换的乘积仍为系统的对称变换。
结合律:三个对称变换的乘积满足结合律,如
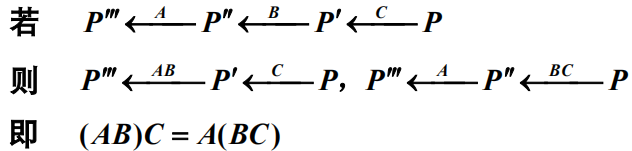
因为对称变换是保持系统不变的变换。
恒元:恒等变换也是一个对称变换,它与任何一个对称变换的乘积仍是该对称变换。
逆元:系统对称变换的逆变换也是该系统的一个对称变换。
4)系统的对称变换群
故系统对称变换的集合构成群(乘法为相继做两次变换),称为系统的对称变换群
5)例:
正三角形所有对称变换的集合构成群,![]() ,所有对称变换只有6个:
,所有对称变换只有6个:

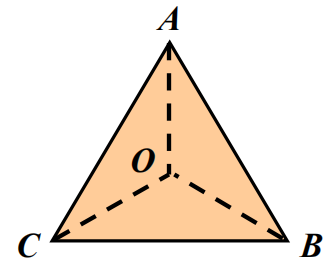
正n边形构成的是群,正4边形对称变换构成的是群,有8个元素。
2.群的定义
群是一个集合,其中定义了元素的“乘积”法则,这个集合G满足4个条件:封闭性、结合律、存在恒元、逆元,这个集合就称为群。(背)
1)封闭性:任何两个元素相乘还在这个集合中(背)
![]()
2)结合律:乘积满足结合律
![]()
3)存在恒元:恒元左乘任意元素,该元素不变。(由后面补充定义知,任意元素乘恒元等于这个元素(背))
![]()
这里只定义了左乘,是否能右乘还需要证明。
4)逆元:存在逆元;元素乘逆元等于恒元。(背)
![]()
只定义了
,是否
成立还需要证明。
群的例子:
验证是群就是要验证4个条件。

例:定义元素的乘法为矩阵乘法,则
GL(n,C)群:全体 n 维非奇异矩阵的集合。
GL(n,R)群:全体n维非奇异实矩阵的集合。
U(n)群:全体n维幺正矩阵的集合。
幺正:
O(n)群:全体n维实正交矩阵的集合。
正交:
,实正交:矩阵元是实数
若限定行列式为1,则上述矩阵的集合分别构成SL(n,C)群、 SL(n,R) 群、 SU(n)群、SO(n)群。
GL:general,C:复数空间,R:实数空间
s:special,O:正交orthogonality,U:幺正
3.群的定义的补充说明
1)群的元素可以是任何客体,如数、矩阵、线性变换、对称操作等;元素的乘法也很宽泛,可以是数的乘法、矩阵的乘法、数的加法、相继的两次变换、相继的两个物理动作等等。
2)物理中常见的群大多是线性变换群、线性算符群或矩阵群,若无特别说明,当元素是线性变换或线性算符时,元素乘积定义为相继做两次变换,当元素是矩阵时,元素乘积取矩阵乘积。
3)右恒元存在且等于左恒元:即成立,即可以左乘
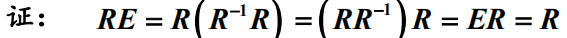
4)右逆元存在且等于左逆元:即成立
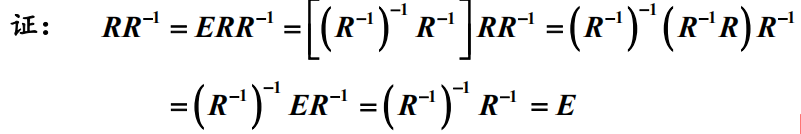
此证明过程也说明的逆元就是R
5)恒元、逆元都是唯一的
证:设一个恒元为E,另一个恒元为T,R为任意一个元素,
则,故只有一个恒元。
同理证:,逆元是唯一的。
6)乘积的逆: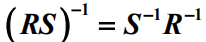
证明:构造
,有
7)阿贝尔群:元素乘积都可以对易的群
(也即交换律成立的群)
非阿贝尔群:能找到两个元素不对易,即除了阿贝尔群之外的群都是非阿贝尔群。
8)有限群:元素数目有限的群
9)有限群的阶:有限群中的元素数目
10)有限群群元素的阶:有限群任一群元素 R 自乘若干次后一定可以得到恒元,满足的最小正整数n称为元素R的阶。(背整个这句话)
一定要理解:R自乘若干次后一定得到恒元,否则就会跑出有限群,就无封闭性,或者对于无限群,可以不用得到恒元。
11)无限群:元素数目无限的群
12)无限分立群:元素数目可数(即可以数出其中几个)的无限群。
13)连续群:元素可以用一组连续变化的参数来描写的无限群。
4.循环群及其生成元
1)循环群:由一个元素 R 及其幂次构成的有限群,记作。(背)
注意是有限群
记住,指的是n阶循环群
n:循环群的阶,即有限群的元素个数。
R:循环群的生成元,因为R可以生成其他元素。
a.n阶循环群的一般形式:
![]()
由此形式知,
b.循环群的性质:
- 循环群的阶和其生成元的阶相等。
生成元的阶是满足
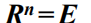 的最小正整数n。
的最小正整数n。 - 循环群都是阿贝尔群(阿贝尔群不一定是循环群)。
元素都是幂次,且结合律,故是元素乘积都可以对易的群。

- 循环群生成元的选择并不唯一,比如 R 和 都可作为群的生成元。但并不意味着谁都可以作为生成元。

c.绕空间固定轴转动角的变换R生成的群
绕空间固定轴转动角的变换R生成的群是一个n阶循环群群![]() 。
。
(这里没有说R是对称变换)
因为由R生成,而验证一个群是循环群还要验证是否
,这里R是转动,确实满足
,故R可以作为生成元,这样的群是一个循环群。
d.n次固有转动轴
n次固有转动轴:若绕空间固定轴转动角的变换R是系统的对称变换,则轴称为n次固有转动轴(n次轴),此时转动R称为n次转动。
说明变换R是保持系统不变
但马书第三版中:”循环群的一个典型例子是由绕空间固定轴转动变换构成的群.按右手螺旋法则,绕轴的正向旋转2n/N角的转动记为Cn.由CN生成的循环群,记为CN.此轴常称为N次固有转动轴,简称N次轴,CN称为N次固有转动,简称N次转动.对二次轴不必规定轴的正向,因为Ch=C^\N次转动和空间反演a的乘积记为SN,SN=aCN=CNa,称为N次非固有转动.由SN生成的循环群记为有时也记为SN,它的阶数g根据N是偶数或奇数,分别是N或2N.此转动轴称为N次非固有转动轴. “
并没有说固有转动轴必须是对称变换,所以ppt中的这个定义可能有问题。
轴的方向:转动R由右手螺旋法则得到,大拇指指向轴的正方向。
二次轴不必规定轴的方向。
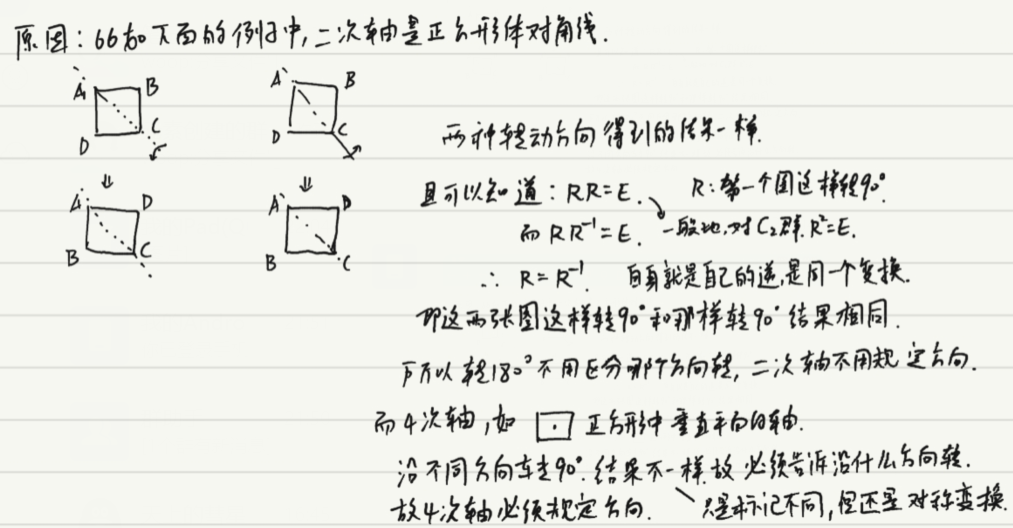
正方形四个角ABCD只是标记,实际上旋转180度后依然是正方形不变(对称变换的定义就是这样,对称变换和ABCD这样的标记无关),并不是说标记变了就是系统变了,故旋转180度的变换R是对称变换。
总结:整个解释好像有些奇怪,没时间,算了。
例:过中心且垂直正方形所在平面的轴是其四次轴,正方形的对角线是其二次轴。
5.有限群的生成元和秩
1)元素R 的周期:由有限群的任一元素 R 及其幂次生成的集合。
循环群由一个元素的周期充满。
一个元素的周期构成的是循环群。
2)有限群的生成元:有限群的群元素可以由最小数目个群元素的乘积生成,这些最小数目个群元素 (背)
称为有限群的生成元。例子见4)
注意最小数目个、群元素
3)有限群的秩:生成元的个数
循环群的秩为1
4)有限群生成元的选择并不唯一,但秩不变。

群的生成元不能是,因为它不能生成群。

群:正三角形的对称变换群。
可以通过画正三角形来验证比如第一行的等式
确实成立。故群的群元素可以由最小数目个群元素D、A的乘积生成,故此有限群群的生成元可以选为D和A,有限群群的秩为生成元的个数2.
但是很重要的一点是:在验证B=DA这种关系时,正三角形的三个字母必须画成:
这种情况,才能验证。若画成
则可以发现验证不了。
6.有限群的重排定理
(考试经常考,简答题,叙述有限群重排定理)
1)复元素:把有限群部分元素的集合看作一个整体
群是一个集合,从这个集合中取一些元素出来再组成一个集合,将这个新集合称为复元素。
- 复元素不考虑所含元素的排列次序,且重复的元素只取一次。
- 两复元素相等的充要条件是它们所包含的元素相同。
- 普通元素与复元素相乘仍为复元素:
设一个普通元素T,复元素,则左乘和右乘都仍为复元素(这个新的复元素仍然属于原来那个有限群,因为群的封闭性):
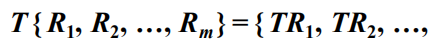
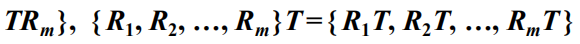
2)重排定理(考试简答题)
设T是群G = {E, R, S, …}中任一确定元素,则下面三个集合与原群G相同 (背)

即(背)
复元素的逆是每个元素取逆
证:集合TG中的所有元素都是群G的元素,故
(这是由于群的封闭性),注意是包含于,所以TG可以比G小。
由于群存在逆元,故在G中,而R也在G中,故也在G中,故
在TG中,是TG中的元素,故
。
综上,TG = G。其它几个关系式可类似证明。
7.同构
在群的定义中,群元素是什么客体并不重要,重要的是它们的乘积规则,也就是它们以什么方式构成群。若两个群它们的元素之间可以用某种适当给定的方式一 一对应起来,而且元素的乘积仍以此同一方式一 一对应,则从群论观点看,这两个群完全相同。
同构的定义:
元素是对应的,在这种对应规则下,元素的乘积也是对应的。群G和同构,
记为。(背)
例:以数乘为乘法的群![]() 同构。
同构。

例:正实数乘法群与实数加法群同构。
如果对应规则选择不适当,则元素的乘积可能不按此规则一一对应,但只要对某一对应规则,两个群符合群同构的定义,它们就是同构的。
8.有限群的乘法表
1)乘法表:
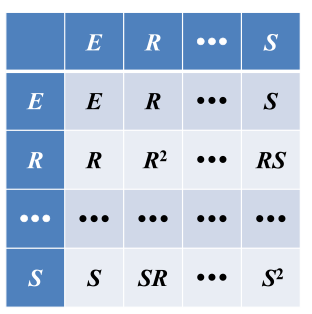
把群元素的乘积全 部 列 出 来 , 构成一个表 , 称为群的乘法表。
对RS=T,称R为左乘元素,S为右乘元素,T为乘积元素。

设群的阶是g,则表内是g×g方阵,每格内填写其所在行的左乘元素与所在列的右乘元素的乘积。
2)乘法表的性质:
- 乘法表完全描写了有限群的性质。
这是因为群的关键就是乘积法则。
- 乘法表相同的两个群同构(若排列次序选择不当,同构的两群可能有看似不同的乘法表)。
因为所有的元素的乘积都包括在其中。
- 由重排定理知,乘法表内各行、各列都是群元素的重排,无重复元素。
3)循环群的乘法表
:群与群同构。故群也称群。
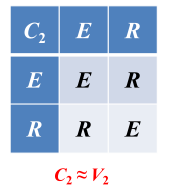
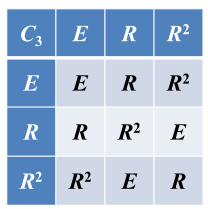



4)四阶群(即有4个元素的有限群)只有两种:若四阶群中含四阶元素,则为群、若四阶群中不含四阶元素,则为群
准确到同构(即从同构的角度看),四阶群(即有4个元素的有限群)只有两种:
- 若四阶群中含四阶元素,则是四阶循环群群;
四阶元素说明,又由于4阶群只有4个元素,故此时只能是四阶循环群群。
- 若四阶群中不含四阶元素,则此群中也不可能含三阶元素;

后面会讲,群中元素的阶一定是这个群的阶的因子,故这里不可能有3阶元素。 - 若四阶群中不含四阶元素,此4阶群只能是一个恒元加3个2阶元素,即此群是群。
一个群中只能有一个1阶元素,即E,所以剩下3个元素一定是2阶元素,故此4阶群只能是一个恒元加3个2阶元素。
综上,四阶群(即有4个元素的有限群)只有两种:群、群。
群:一个恒元加3个2阶元素。其为:

群的乘法表:

由于是二阶元素,故
5)准确到同构,六阶群只有两种:若含六阶元素,则是群、若不含六阶元素,则是群。
- 若含六阶元素,则是群;
- 若不含六阶元素,则不可能含五阶、四阶元素;
后面会讲,群中元素的阶一定是这个群的阶的因子,故这里不可能有4、5阶元素。
- 若不含六阶元素,从群含的三阶元素的个数分类:
- a.含零个三阶元素,即群只含一个恒元加5个二阶元素。这种情况不成立。


作业第3题:
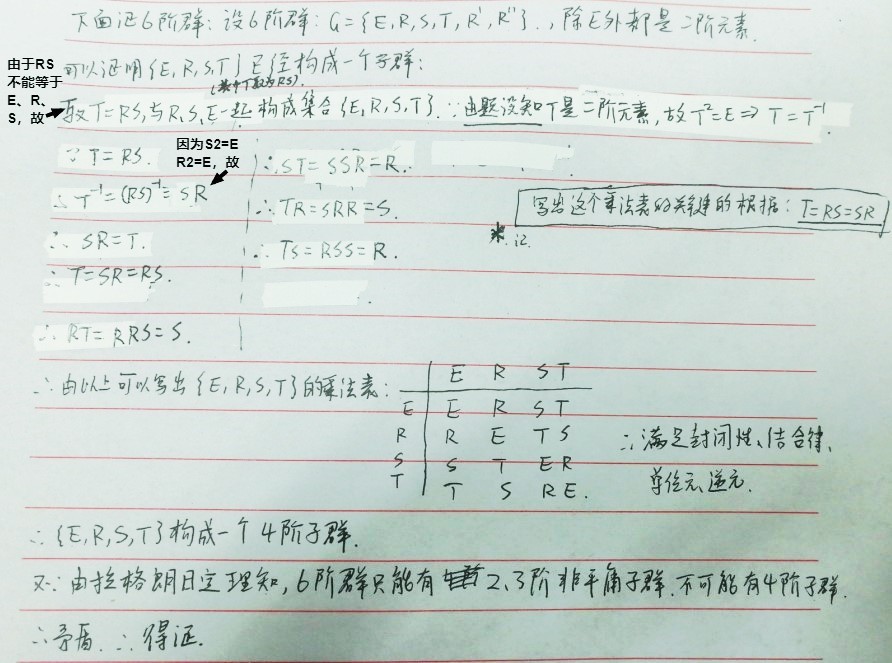
- b.含两个三阶元素,三个二阶元素,1个恒元。
含2个三阶元素是因为若含1个三阶元素,则一定至少含2个三阶元素。且群只能含偶数个三阶元素。
在b.的情况下,该群是群(正三角形对称变换群):一个恒元加两个三阶元素加三个二阶元素;
“若含1个三阶元素,则一定至少含2个三阶元素。且群只能含偶数个三阶元素。”是因为:

- c.含四个三阶元素,一个二阶元素,一个恒元。这种情况不成立。

- a.含零个三阶元素,即群只含一个恒元加5个二阶元素。这种情况不成立。
综上,六阶群只有两种:群、群。
群(正三角形对称变换群)
其乘法表:

此乘法表的得出和a.情况中讨论的群的乘法表的得出类似
群是最简单的非阿贝尔群。
二阶群只有群,三阶群只有群、四阶有两个:群、群、五阶群只有群,由这些群的乘法表知(乘法表沿对角线对称),二阶、三阶、四阶、五阶的群都是阿贝尔群。
而由上面群的乘法表知,元素乘积存在不对易,故是最简单的非阿贝尔群。最简单指的是阶数最少。
6)正N边形对称变换群——群
对称变换轴:1个N次轴,N个二次轴。
1个N次轴是指垂直于正N边形所在平面的一个轴,N个二次轴是指在正N边形所在平面内的轴。
举例说明:正四边形,有1个四次轴,4个2次轴。
在N分别是奇数偶数时,二次轴的情况不同:

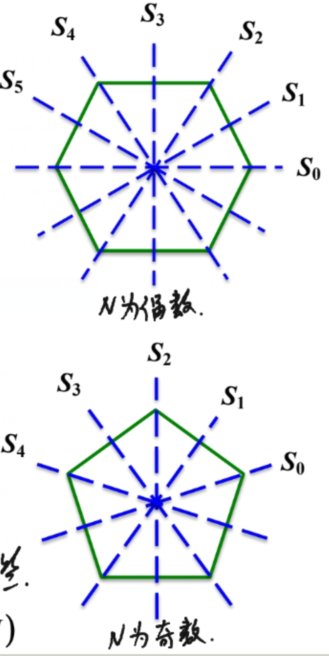
绕N次轴转动的对称变换的集合:

N次轴:垂直于正N边形所在平面的一个轴。
绕N次轴转动的对称变换的集合构成一个周期(N阶循环群)。
这个集合有N个元素。
绕N个二次轴转动的对称变换的集合:
这个集合有N个元素。
由于以上两个集合都各有N个元素,故群有2N个元素。
群的乘法表
为求乘法表,先证明![]()
![]()
举例说明:对上面图中的正五边形,T:转,:关于这个轴翻180度。
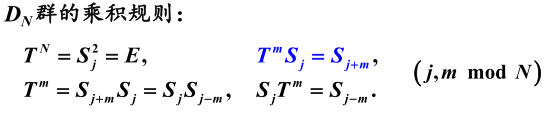
只需要知道公式(1)和(2)就能推导出另外两个乘积规则的公式。所以只要背乘积规则中的前两个公式、,就能推导出另外两个乘积规则的公式。(背)
群的阶为2N,秩为2,生成元可取T,
由前面乘积规则知,有T,就能得到其他所有元素
2N个元素,故群的阶是2N;两个生成元,故秩为2;
由上面乘积规则可以得到乘法表:

1.2节 群的各种子集
1.子群
1)定义:群 G 的子集 H,若按照原来的元素乘积规则,也满足群的四个条件,则称为群G的子群。(背)
如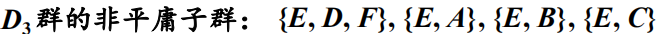
可以验证这些是群。
2)判断有限群的子集是否构成子群,只需检验子集是否满足封闭性即可:
子集元素采用原群的乘法,结合律显然满足;若子集对元素乘积封闭,则它必包含子集中任一元素的周期,从而包含恒元和逆元。任何群都有两个平庸的子群:恒元和整个群。
3)任何群都有两个平庸的子群:恒元和整个群。
4)任一元素的周期构成循环子群,与阶数相同的循环群同构。
比如群中的
5)寻找有限群的子群的最好办法:(背)
a.列出全部循环子群
b.把若干个循环子群并起来
c.看它们是否满足封闭性(判断是否满足封闭性:判断其中每一个元素的周期是否都在里面,再判断某两个元素的乘积是否会出去)。恒元、拉定理、封闭性。
原因:寻找子群就是要满足封闭性,满足封闭性最重要的就是要包括每一个元素的周期,即循环子群,但还应判断某两个元素的乘积是否会出去。故以上方法成立。
6)常见群的子群的例子
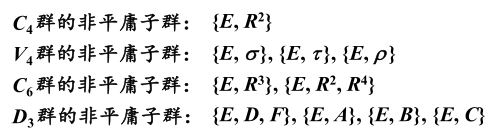
我通过上面“寻找有限群的子群的最好办法”求出了确实这些群的子群是这些。
2.陪集和不变子群
1) 左陪集 和 右陪集
设 群G 的阶 为g ,子 群H 的阶 为h ,子 群H 记 为
![]()
任取群G中不在子群H中的元素,把它左乘或右乘到子群H上(背),得到群G的两个子集

左陪集:![]()
右陪集:![]()
左陪集和右配集中第一个元素都是
2)陪集的性质
- 陪集中没有恒元,所以陪集一定不是子群

- 陪集与子群无公共元素。
- 一个陪集中没有重复元素。
这两个性质证明:

- 两个有公共元素的左陪集必然全相同。

注意其逆否命题:不相同的左陪集没有公共元素
- (背,重要性质,很有用)有限群G一定可分解为子群H和若干个左陪集之并,这些子集间没有公共元素,每个子集包含h个不同元素:
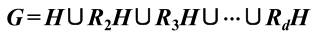
这里说的若干个左配集都是不同的左陪集。

由于陪集和子群元素个数相同,故都是h个元素。
由这个性质可以直接得到下面的拉格朗日定理。 - 群G中两元素R和T都在同一左陪集RH的充要条件是
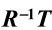 在子群H中。(即
在子群H中。(即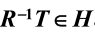 )
)
证明:


3)拉格朗日定理:群G的阶数g是其子群H阶数h的整数倍(即子群的阶数是群G的阶数的因子(背,考试简答题)),g=dh,其中d称为子群H的指数。
![]() 群的阶数为素数的群没有非平庸子群。群的阶数为素数的群只有一种,就是循环群,群中除了恒元以外,其他所有元素的阶都是该素数。
群的阶数为素数的群没有非平庸子群。群的阶数为素数的群只有一种,就是循环群,群中除了恒元以外,其他所有元素的阶都是该素数。

由此也知,3阶群、5阶群、7阶群等阶数为素数的群都是只有一种,就是、、群等。
拉格朗日定理的证明见上面倒数第二个性质。
4)不变子群
用群G中不在子群H中的一个元素,左乘和右乘子群H,得到的左陪集和右陪集不一定相同。
不变子群:
若子群H的所有的左陪集都和对应的右陪集相等(背),即对群G中不在子群H中的任意一个元素,都有,则此子群H是原群G的不变子群H,或称为正规子群。
注意:一个子群是不变子群并不要求Rj和H中的元素对易,即并不意味着乘H中的元素等于H中的元素乘以。
因为可能是乘H中元素T等于H中元素S乘。
5)不变子群的性质
a.阿贝尔群的所有子群都是不变子群(背)。
证明:因为阿贝尔群所有元素都是对易的,从左边乘和从右边乘对每一个元素来说都一样,故子群H的所有的左陪集都和对应的右陪集相等,故是不变子群。
例子:前面说了,二阶、三阶、四阶、五阶的群都是阿贝尔群,故其子群都是不变子群。
群由于是循环群,故其是阿贝尔群,故其子群是不变子群。
b.指数为2的子群一定是不变子群(背)。

例子:
c.不变子群与类的关系:不变子群必然由若干个完整的类组成 (背)。由若干个完整的类组成的若是一个子群,则必然是不变子群。(这个性质可以用来判断不变子群)
证明:见后面。
6)商群
商群:不变子群H及其所有不同的陪集,构成一个复元素的集合,定义复元素的乘积规则:,在下面的注释中我们验证了这个复元素的集合满足群的四个条件,故此集合为群。这个由复元素构成的群称为群G关于不变子群H的商群,记作G/H
商群的恒元是不变子群H。
商群的阶数是不变子群H的指数。

由于不变子群及其所有不同的陪集构成商集,而不变子群及其所有不同的陪集并起来就是群G,陪集的元素个数和子集的元素个数相等,不变子群阶数为h,群G阶数为g,则由拉定理:g=dh,故指数d也就是商群中复元素的个数,即商群的阶数。
例子:

7)从乘法表找子群的陪集:
设群G的子群H,群G的乘法表中与子群H的元素有关的各列中,每一行的元素要么构成子群,要么构成左陪集;G的乘法表中与子群H的元素有关的各行中,每一列的元素要么构成子群,要么构成右陪集。(背)
例如:从D3群的乘法表找出各子群的陪集。
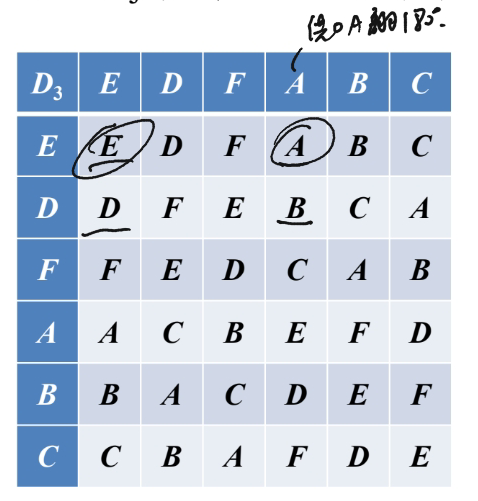

(考试和作业中经常有这个题,随便给一个群进行分析,记住这个例题的过程)求群的所有子群及其陪集,判断不变子群:
先由拉定理知,子群的阶数只能是2或3.
当子群阶数是3时,由于3阶群只有一种:群,而由于群是一个恒元加两个三阶元素,故这里的3阶子群只能是{E,D,F},D,F才是三阶元素。由于{E,D,F}指数是2,故其是不变子群。
当子群的阶数是2时,除了恒元外,为满足封闭性,另一个元素一定是二阶元素,故这里的2阶子群是{E, A}、{E, B}、{E, C}。
注意分析子群阶数、元素的阶数。
由乘法表可以写出{E, A}、{E, B}、{E, C}的陪集,由于所有左陪集和右陪集并不对应相等,故它们不是不变子群。
3.共轭元素和类
1)共轭
定义:对群G中的两个元素和,如果在群G中存在一个元素S,使得和可以通过联系起来,则称和共轭,记为 (背)
共轭的性质:
- 相互性:则
- 传递性:与同一元素共轭的元素也相互共轭:,则。由共轭的传递性可以定义类。
证明:两个性质的证明见李书16页
2)类
a.定义:所有相互共轭的元素形成的集合,记作
其中是类中所包含的元素数目。
b.类的性质
- 一个类可以被其中任意一个元素所确定。寻找类中所有元素的方法:对一个类中元素R,取群G中的一个元素S,求出,当S取遍G中的所有元素时,R的所有同类元素就一个一个都出现了
- 恒元自成一类

- 阿贝尔群的每个元素自成一类。

由此性质知,群是阿贝尔群,有两个元素,故两个类。群:时间反演等,它是阿贝尔群,四个元素,故4个类。
- 两个类没有公共元素;
证:若两个类有公共元素,则所有元素都互相共轭,它们应在一个类,故两个类没有公共元素。
- 除了恒元构成的类以外,类不是子群。
证:由上一个性质知,其他类不包含恒元,故其他类不是子群。
- 群按陪集分割:子群和陪集元素数目相同;群按类分割:每个类中所含元素数目不一定相同(通常来说肯定不同)。

群按类分割:通常来说肯定不同,除非特殊情况,比如二阶群,R一类,E一类、还有阿贝尔群,每个元素自成一类,但非阿贝尔群通常来说每个类元素数目不同。 - 同类元素的阶相同(但阶数相同的元素不一定在同一类)

阶数相同的元素不一定在同一类:比如群,除E外每个元素都是5阶的,但它们不在一个类。再比如后面会说到的D4群中,S0和S1都是二阶元素,但它们不在一个类。 - 对任意 给 定 的
 , 当Rj 取 遍 类
, 当Rj 取 遍 类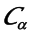 中的所有元素时 ,
中的所有元素时 ,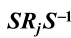 一定不 会 重 复 ,故
一定不 会 重 复 ,故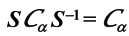

注意当Rj 取 类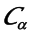 中的一个元素时,
中的一个元素时,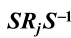 也是类中的一个元素。故得证。
也是类中的一个元素。故得证。 - 对任意给 定 的
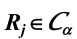 , 当S 取 遍 群G 中的所有元素时 ,
, 当S 取 遍 群G 中的所有元素时 ,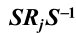 有重 复 , 但
有重 复 , 但 的重 复次数对 每 一 个
的重 复次数对 每 一 个 都 是一样的,均为
都 是一样的,均为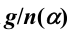 。
。
g:群G中元素个数。
:这个类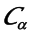 中的元素个数。
中的元素个数。
举例说明这个性质:

证明:对给定的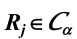 ,
,


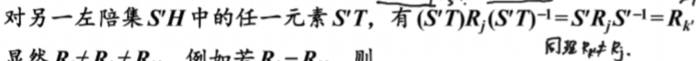
注意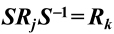 与T无关,而
与T无关,而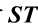 中的S是给定的,T是任意的,故对左陪集SH中的任一元素ST,得到的结果都是
中的S是给定的,T是任意的,故对左陪集SH中的任一元素ST,得到的结果都是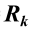
 。
。
 ,下面证明
,下面证明 :
:
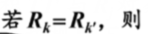
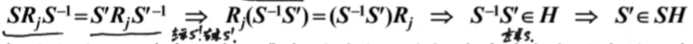

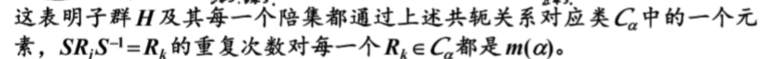
经过思考,上面这个结论确实成立。注意的含义:与给定元素Rj对易的所有元素的集合构成群G的子群H,将该子群的元素个数记为。
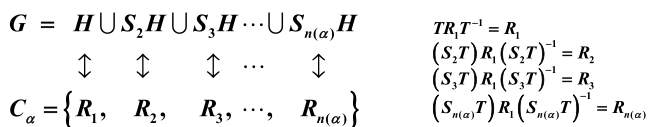
由上面这个对应知,类中包含的元素数目是(与给定元素Rj对易的所有元素的集合构成群G的)子群H的指数,故类中包含的元素为: ,由此式得:重复次数为
,由此式得:重复次数为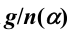 。得证。
。得证。
由拉定理知,子群H的指数是群G阶数的因子,故类中包含的元素也是是群G的阶数g的因子。
3)相逆类、自逆类
如果一个元素Rj和Rk在一个类![]() 中,则Rj的逆和Rk的逆也一定会在一个类
中,则Rj的逆和Rk的逆也一定会在一个类![]() 中,但这个类
中,但这个类![]() 与类
与类![]() 是否相同并不知道。
是否相同并不知道。
证明:当Rj和Rk在一个类中时,即群G中存在S,使得
,则对此式两边取逆,得
,说明
和
在一个类中,即如果一个元素Rj和Rk在一个类
中,则Rj的逆和Rk的逆也一定会在一个类
中。
由上面可以知道,类![]() 中的所有元素的逆组成一个集合,这个集合构成类,记作类
中的所有元素的逆组成一个集合,这个集合构成类,记作类![]() 。类
。类![]() 与类
与类![]() 称为相逆类(背),它们的元素数目相同。
称为相逆类(背),它们的元素数目相同。
相逆类:这个类是那个类所有元素的逆构成的。
自逆类:若元素与其逆元素互相共轭,则类![]() 与类
与类![]() 重合(背),这样的类称为自逆类。
重合(背),这样的类称为自逆类。
举例说明:

4)用乘法表判断两元素是否共轭、用乘法表找出类:
元素ST和元素TS互相共轭:
![]()
故ST和TS在一个类中。注意TS和ST在乘法表中关于对角线对称,故乘法表中关于对角线对称的元素在一个类中。
互相共轭的两元素总可以表示为某两元素不同次 序的乘积:
![]()
![]()
因此若乘法表中左乘元素和右乘元素顺序相同,则在乘法表中关于对角线对称的两元素互相共轭。互相共轭的两元素也一定在乘法表中关于对角线对称的位置出现。关于对角线对称的元素在一个类中,由此就可以根据乘法表找出类。
因为关于对角线对称的一定是一个是ST,一个是TS。
举例说明:


根据关于对角线对称的元素在一个类中,可以知道B、C、A在一个类中,D、F在一个类中。
5)系统对称变换群群的类
设n方向是系统的N次固有转动轴,元素R是绕n方向转动2pi/N角的变换。
设元素S将n方向转到m方向,设此元素S在系统的对称群中。
则元素![]() 表示绕m方向转动2pi/N角的变换。
表示绕m方向转动2pi/N角的变换。
证明:

实际上这里需要第五章转动群的知识才懂。确实。
由于S是对称群中的元素,由封闭性知,也是对称群中的元素。根据共轭的定义:"对群G中的两个元素和,如果在群G中存在一个元素S,使得和可以通过联系起来,则称和共轭"知,R与![]() 共轭。
共轭。
由于R与![]() 共轭,故绕n方向和绕m方向转动2pi/N角的变换是互相共轭的。
共轭,故绕n方向和绕m方向转动2pi/N角的变换是互相共轭的。
![]() 表示绕m方向转动2pi/N角的变换,m方向显然也是系统的N次转动轴。
表示绕m方向转动2pi/N角的变换,m方向显然也是系统的N次转动轴。
原因:由于R是绕n方向转动2pi/N角的对称变换,
表示绕m方向转动2pi/N角的变换,它们相互共轭,是同类元素,由于同类元素的阶相同,故R的阶数是N,故
的阶数也是N,即m方向是N次固有转动轴。(由于前面证明了也是系统的对称群中的元素,故
也是对称变换,故m方向是N次固有转动轴)
a.等价轴:一般地,若两个同次轴的正方向可以通过对称群中的元素联系起来,则这两个转动轴称为等价轴。(背)
注意,这里等价轴定义中说的的对称群是这个形状对应的对称群,具体见后面“同次轴不一定是等价轴”的证明过程中的解释。
若绕x、y、z转90度是对称群中的元素,且三维坐标系中的x、y、z是同次轴,则三维坐标系中的x、y、z就是等价轴,因为绕y方向转90度,z就变到x;绕z转90度就是x变到y;绕x转90度就是y变到z,故它们等价。
等价轴一定是同次轴,但同次轴不一定是等价轴。
因为等价轴的定义中就是说等价轴是用同次轴定义的。
刚才已经证明了n和m方向是同次轴,而因为n和m是同次轴,且它们可以通过元素S联系起来,若S是对称群中的元素,则n和m就是等价轴。
同次轴不一定是等价轴:

而群中当N为奇数时,N个二次轴都是等价的。
b.双向轴(非极性轴):
若一个轴的正反两个方向可以通过对称群中的元素联系起来(背),则此轴称为双向轴,或非极性轴。
c.等价轴、双向轴的性质:
- 二次轴没有极性的概念,注意:不考虑二次轴是否双向轴(背)
- 绕等价轴转相同角度的变换互相共轭。(背)
证明:由于等价轴,故由等价轴的定义知,将n变到m方向的元素S一定在对称群中,前面说元素R是绕n方向转动2pi/N角的变换,表示绕m方向转动2pi/N角的变换;由于S是对称群中的元素,由封闭性知,也是对称群中的元素。根据共轭的定义:"对群G中的两个元素和,如果在群G中存在一个元素S,使得和可以通过联系起来,则称和共轭"知,R与
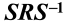 共轭。故得证。
共轭。故得证。 - 绕双向轴正转、逆转相同角度的变换互相共轭。(背)
绕双向轴正转、逆转相当于一个绕n方向转,一个绕m方向转。由双向轴的定义知,双向轴是等价轴的一个特例,且由于上一个性质,故得证。
- 转动不同角度的变换一定不共轭;绕非等价轴转相同角度的变换也不共轭。
老师没解释,我没时间,算了。
d.举例:D3 群、D4群的类:通过(1)分析轴是几次的、(2)轴是双向轴还是等价轴,(3)再通过等价轴、双向轴的两个性质就能判断类。
例 :D3 群的类
D3 群 包 含1 个三次轴 和3 个 二 次轴 。
绕 二 次轴的转动使三次轴是双向轴 , 绕三次轴的转动使3个二次轴互相等价 。
一个轴的正反两个方向可以通过对称群中的元素联系起来则是双向轴,这里绕 二 次轴的转动就是“对称群中的元素”,故三次轴是双向轴。
由于二次轴没有极性,故不考虑二次轴的方向。
D3 群有3个类:恒元一个类,绕三次轴转动一个类,绕二次轴转动一个类。
恒元自成一类{E} 。
绕三次轴正 、 逆 转2pi/3 角 的D 和F 构成一 类{D, F} 。
绕 二 次轴转动 的A ,B 和C 构成一 类{A, B, C} 。
因为“绕双向轴正转、逆转相同角度的变换互相共轭”,三次轴是 双 向轴,故绕三次轴正 、 逆 转2pi/3 角 的D 和F 构成一 类{D, F}。类:所有相互共轭的元素形成的集合。
因为“绕等价轴转相同角度的变换互相共轭”,3个二次轴互相等价,故绕 二 次轴转动 的A ,B 和C 构成一 类{A, B, C}。
例:D4群的类
D4群包含1个四次轴和4个二次轴。
绕二次轴的转动使四次轴是双向轴,绕四次轴的转动使4个二次轴分成两组(对角线连线和对边中点连线),分别互相等价。
D4群有5个类:恒元一个类,绕四次轴转动分为两个类,绕二次轴转动也分为两个类。
恒元自成一类{E}。
绕四次轴正、逆转pi/2的T和构成一类![]() ,绕四次轴正、逆转pi的构成一类{}。
,绕四次轴正、逆转pi的构成一类{}。
绕二次轴对角线转动的S0和S2构成一类![]() ,绕对边中点连线转动的S1和S3构成一类
,绕对边中点连线转动的S1和S3构成一类![]() 。
。
因为“绕双向轴正转、逆转相同角度的变换互相共轭”,四次轴是 双 向轴,故绕四次轴正、逆转pi/2的T和构成一类
(正转270度就是逆转90度),绕四次轴正、逆转pi的构成一类{}。
S0和S2可以通过对称群中的元素“转90度”而等价,S1和S3也可以通过对称群中的元素“转90度”而等价。但S0和S1这两种不等价,前面“同次轴不一定是等价轴”有解释。由于绕等价轴转相同角度的变换互相共轭,故S0和S2构成一类,S1和S3构成一类
。
6)寻找有限群的类和不变子群的步骤
a.不变子群与类的关系:不变子群必然由若干个完整的类组成 (背)。由若干个完整的类组成的若是一个子群,则必然是不变子群。(这个性质可以用来判断不变子群)
证明:

不变子群的左陪集和右陪集相等 , 所以它 包含每 个元素的共轭元素 , 因 此 , 不变子群必然是由若干个 完 整的类组成 。
b.寻找有限群的类的步骤:
法一:从乘法表判断两元素是否共轭、从乘法表来寻找
法二:从“同类元素的阶相同”来寻找
(1)先确定每个元素的阶(即判断多少次方等于E),
(2)在阶数相同的元素中判断其是否共轭,从而找到所有共轭类。
c.寻找有限群的不变子群的步骤:
法一:根据乘法表和不变子群的性质、定义(所有左陪集都和对应的右陪集相等)来寻找,见不变子群一节的7)从乘法表找子群的陪集。
法二:根据“不变子群必然由若干个完整的类组成(背)”来寻找。
(1)将若干个类并起来
(2)判断其是否构成子群(若构成子群,则是不变子群):
- 是否包含恒元
- 是否满足拉定理:子群的阶数是群阶数的因子
- 是否包含每一元素的完整周期,是否满足封闭性
法三:若已经知道了子群,则从子群中根据“不变子群必然由若干个完整的类组成(背)”来寻找。
例 :D3 群的非平 庸 不变子 群 {E, D, F}

子群可能是1,2,3,6阶。不变子群还有(E,D,F,A,B,C}
例 :D4 群的非平 庸 不变子 群 {E, T2} {E, T, T2, T3} {E, T2, S0, S2} {E, T2, S1, S3}

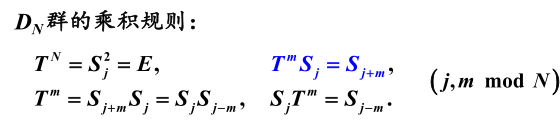
已知乘积规则中的前两个公式、,就能推导出其他两个乘积规则,所以可以推导出来。
7)系统对称变换群群的类和不变子群
所有群都有一个N次轴,N个二次轴。
N为偶数时,即N=2n:一个N次轴是双向轴,N个二次轴分成两组(对角线和对边中点连线),分别互相等价。比如群.
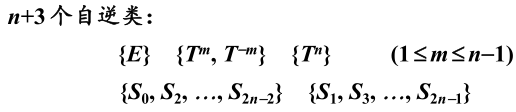
对正N边形,只要有二次轴,则这个N次轴就是双向轴,是双向轴则正转、逆转相同角度都在一个类中,对群,绕4次轴转有三个类:恒元、正转和逆转90,转180. 对,绕6次轴转有4个类:恒元、1次方和5次方、2次方和4次方、3次方。
找规律:,绕8次轴转有5个类,故群,绕N次轴转有n+1个类;而绕二次轴转有两个类,故一共有n+3个类:
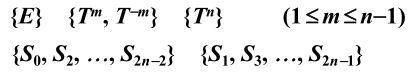
且可以验证这n+3个类是自逆类。
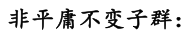
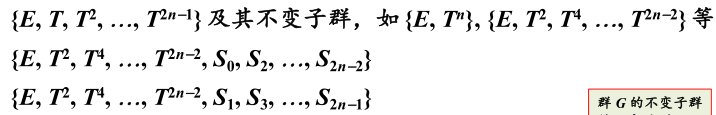

>

老师通过举群的例子说明了这些不变子群:

群的例子:
N为奇数时,即N=2n+1:一个N次轴是双向轴,N个二次轴互相等价。
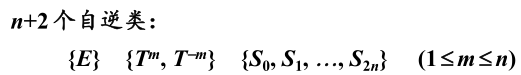
其推导类似前面N为偶数时的推导。
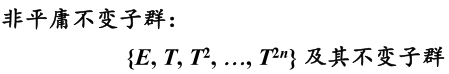
举例:

1.3节 群的同态关系
1.群的同态:
若群和G的所有元素间都按某种规则存在一多对应关系,它们的乘积也按同一规则一多对应,则称群与群G同态,记为。
群与群G中的元素是一多对应的,在这种对应规则下,元素的乘积也是一多对应的。(背)
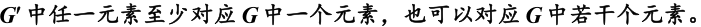
。这句就是说同态是有方向性的,说明G中的元素多一些。
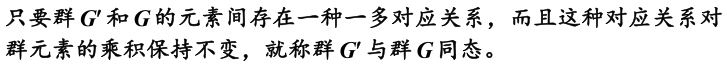
找到一种对应关系即可。
同态的性质:
- 同态有方向性:说明G中的元素多一些。(因为群与群G中元素是”一多对应的“,背,重要)

- 同构是一种特殊的同态,
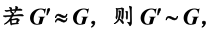 反之,同态则不一定同构。
反之,同态则不一定同构。 - 只包含恒元的一阶群与任何群同态。

- 同态的例子:(背这个例子中对应规则的写法,重要)
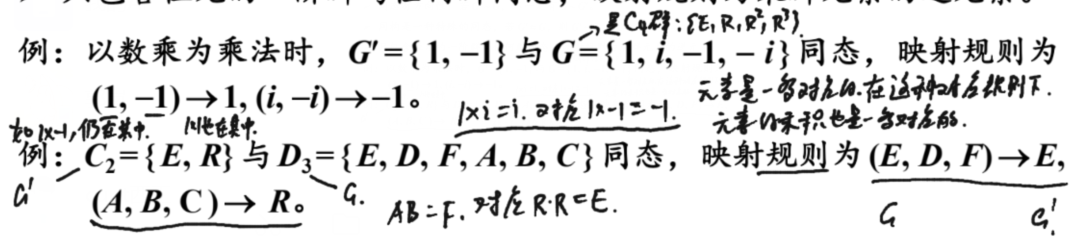
2.同态核定理:若G‘与G同态,即G‘~G,则与G‘恒元对应的G中元素的集合H构成群G的不变子群,与G’其它每一个元素相对应的G中元素的集合构成H的陪集,即群G’与群G关于H的商群同构,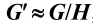 ,H称为同态对应的核。
,H称为同态对应的核。

复习:商群:不变子群H及其所有不同的陪集,构成一个复元素的集合,定义复元素的乘积规则:,在下面的注释中我们验证了这个复元素的集合满足群的四个条件,故此集合为群。这个由复元素构成的群称为群G关于不变子群H的商群,记作G/H
商群的恒元是不变子群H。
商群的阶数是不变子群H的指数。

证明同态核定理:

3.集合G‘与群G的同构或同态
讲同态和同构定义时说是群,但实际上不需要强调是群,我们可以证明它一定是群。
以后我们会遇到这种情况,其中一个是一堆元素的集合G‘(是一个定义了乘积规则的集合),另一个是群G,若集合G‘和群G中的元素是一一或一多对应的,在这种对应规则下,元素的乘积也是一一或一多对应的,则一堆元素的集合G‘也是一个群,是与群G同构或同态的群。(背)
设G‘是一个定义了乘积规则的集合,G是一已知群,若群G中任一元素R都按某种规则唯一地对应集合G‘中的一个确定元素R‘,而集合G‘中任一元素R‘至少对应群G中的一个元素R,且这种一一对应或一多对应的关系对元素乘积保持不变,则集合G‘构成群,且与已知群G同构或同态。
证明:
1.4节 正多面体的固有对称变换群
1.固有转动:三维空间中保持坐标原点不变、保持手性不变、保持任意两点间的距离不变的转动称为固有转动。
保持手性不变:就是说左手系还是左手系,右手系还是右手系,这意味着转动不包含空间反演,如果有空间反演的话,左手系会变成右手系,右手系会变成左手系。见第五章。
2.非固有转动:若转动后再做空间反演,则坐标系的手性会发生改变,
这样的转动称为非固有转动。
非固有转动仍保持坐标原点不变、保持任意两点间的距离不变。
3.点群:让体系的一个点保持位置不变的操作构成的变换群。
4.固有点群:由固有转动的集合构成的有限群称为固有点群,包括群、群及正多面体固有对称变换群。
固有点群是SO(3)群的有限子群。
在三维空间中的转动是SO(3)群中的元素,故固有点群是SO(3)群的有限子群。
SO(3)群:三维空间实正交矩阵的集合,也可以理解为三维空间所有转动变换的集合构成的群。(不包括空间反演)
O(n)群:全体n维实正交矩阵的集合。S:行列式为1.
正交:,实正交:矩阵元是实数
5.非固有点群:由固有转动和非固有转动的集合构成的有限群称为非固有点群。即包含非固有转动的群。
非固有点群是O(3)群的有限子群。
非固有点群一定包含若干固有转动元素,因为至少恒元是固有转动元素。
O(3)群:三维空间的所有转动+空间反演。故非固有点群是O(3)群的有限子群。
由于SO(3)群是三维空间所有转动变换的集合构成的群,故SO(3)是O(3)的子群。
6.正多面体
1)定义:各个面都是全等的正多边形的多面体
下面计算到底有多少个正多面体
设正N面体有N个面,每个面是正n边形;
设正N面体一共有L条棱和V个顶点,每个顶点出发有m条棱和m个侧面;(比如一个顶点有三条棱,则有三个侧面)
正N面体有N个面,每个面是正n边形,考虑到正N面体每条棱由两个侧面所共有(会导致计算棱数时会重复),故![]() 就是棱数;正N面体有V个顶点,每个顶点出发有m条棱,考虑到每条棱联结两个顶点,故
就是棱数;正N面体有V个顶点,每个顶点出发有m条棱,考虑到每条棱联结两个顶点,故![]() 也等于棱数。故棱数:
也等于棱数。故棱数:
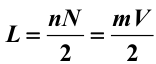
正n 边 形每个内角为(n-2)pi/n,一个顶点必须至少出来三个棱才能组成正多面体。每个顶点出来m个面,故角度:![]() ,其应该小于2pi。故正多面体每个顶点出发的面数m应满足:
,其应该小于2pi。故正多面体每个顶点出发的面数m应满足:
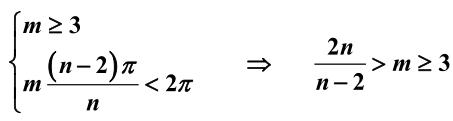

从一个顶点出发有5个棱,只能是正三边形。
正N面体的内角和为:
有N个面,每个面内角和是(n-2)pi,故正N面体内角和:![]() ,由前面棱数公式知nN=2L,故正N面体的内角和为:
,由前面棱数公式知nN=2L,故正N面体的内角和为:![]() 。
。

两种办法得到的内角和相等,于是有(欧拉公式):
![]()

代入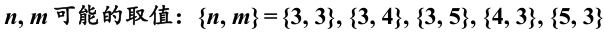
2)可能的正多面体及其参数
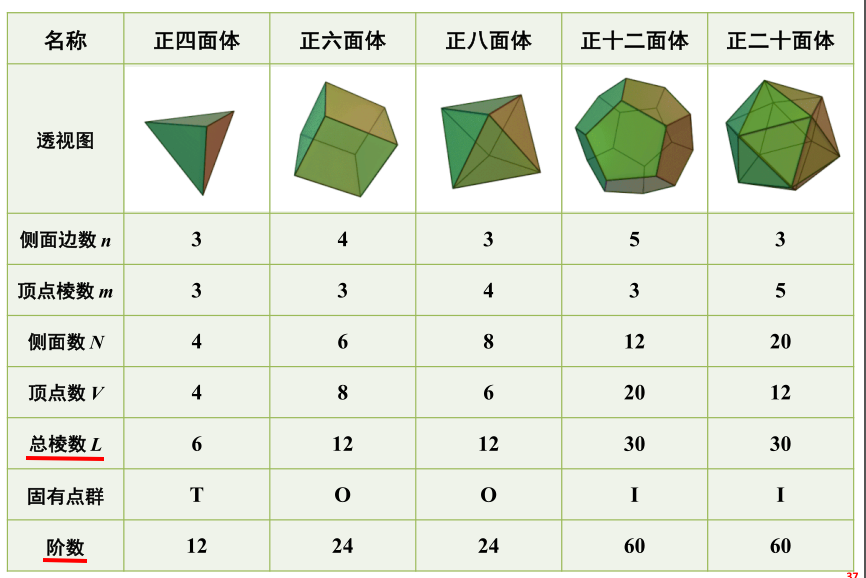
正多面体只有5种。
正多面体的所有对称变换群只有这三种:T、O、I群
3)对偶正多面体:将正多面体各个侧面的中心作为顶点联结起来构成的图形也是正多面体,称为原正多面体的对偶正多面体。
- 正四面体与自己对偶,是自对偶图形;正六面体的对偶图形是正八面体,注意互相对偶;正十二面体的对偶图形是正二十面体。

- 对偶关系是相互的。
- 由前面正六面体的例子知,两对偶正多面体的面数N和顶点数V互换,侧面边数n和在每个顶点交会的棱数m互换,总棱数L保持不变。
a.如果两个正多面体互相对偶,则它们的对称变换群相同。(背)
由前面正六面体的例子知,如果所有的对称操作保持正八面体不变的话,也会保持正六面体不变,故对称变换群形同。
b.T群、O群、I群
T群:正四面体的固有点群
O群:正六面体和正八面体的固有点群
I群:正十二面体和正二十面体的固有点群
c.正N面体的固有点群的阶数为2L。L:棱数
把正多面体的中心放在坐标原点,正多面体的位置可由一条棱的位置来确定,只注意这个棱,每个对称变换可由这条棱在变换后的新位置来描写。经过对称变换,这条棱可置于L条棱中的任一条位置,再考虑棱的两种取向,则正N面体的固有点群的阶数为2L。L:棱数
棱有多少个位置,正多面体的固有点群就有多少个对称变换元素。
7.正四面体固有点群—T群
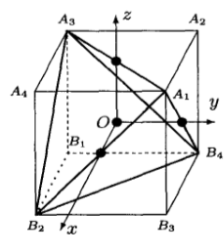
建立如图所示的坐标系。将立方体不相邻的顶点联结起来构成正四面体。
正四面体的对称变换都是立方体的对称变换,但立方体的对称变换不一定都是正四面体的对称变换。因此,正四面体的固有点群T群是立方体固有点群O群的子群。
- 3个坐标轴是正四面体的二次轴
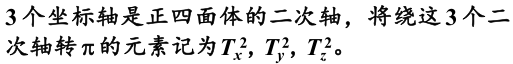
因为绕这3个轴转pi,不变,故是二次轴。
- 立 方 体 的4个体对角线是正四面体的三次轴

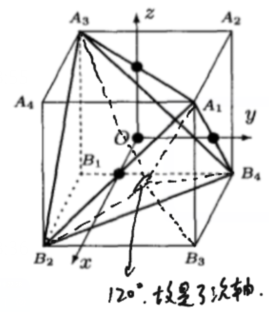
- 正四面体三次轴的转动使3个二次轴等价,二次轴的转动使4个三次轴等价,但三次轴不是双向轴。
3个二次轴等价:
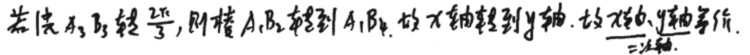
4个三次轴等价: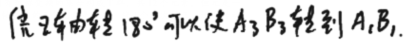
三次轴不是双向轴:经验证,没有对称群中的元素能使A3、B3换一个方向,故立方体的体对角线不是双向轴。
二次轴不考虑方向。 - 正四面体所有固有对称变换的集合构成T群,T群有12个元素:恒元+3个二次轴给出的3个元素+每个三次轴给出2个元素,4个三次轴共给出8个元素=12个元素。
- T群的类:
恒元是一类,
绕3个二次轴转动的3个元素是一类,(由于3个二次轴等价,绕等价轴转相同角度的变换在一个类中)
绕4个三次轴正、逆向转动的8个元素分成两类:绕4个三次轴正转2pi/3的元素在一个类中,逆转2pi/3的元素在一个类中。
(由于4个三次轴等价,绕等价轴转相同角度的变换在一个类中)
故T群有4个类。前2个类是自逆类,后2个类是相逆类。
后面讲不等价不可约表示时,有几个不等价不可约表示就取决于几个类,4个类故T群有4个不等价不可约表示。
- T群的乘法表

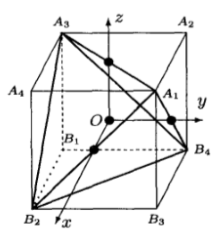
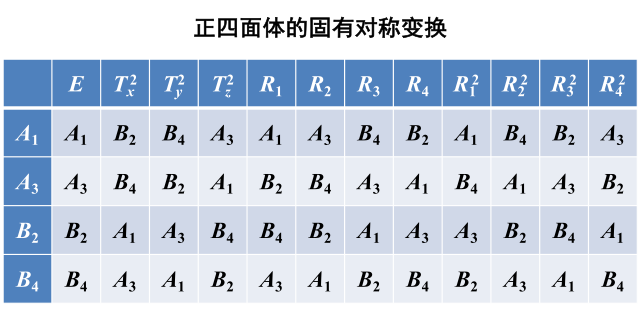
从此表可以知道这12个元素作用于这个正四面体,得到的新的点的位置。

类似的这样的方法就可以得到所有元素的乘积,再得到乘法表。
- T群的子群、不变子群:

这个不变子群是一个恒元加三个二阶元素,故是群(E,时间反演,空间反演,时空全反演)。
找子群:先找每个元素的周期,再将每个元素的周期并起来,看是否满足封闭性。恒元、拉定理、封闭性。
寻找有限群的不变子群的步骤:
法一:根据乘法表和不变子群的性质、定义来寻找,见不变子群一节的7)从乘法表找子群的陪集。
法二:根据“不变子群必然由若干个完整的类组成(背)”来寻找。
(1)将若干个类并起来
(2)判断其是否构成子群(若构成子群,则是不变子群):是否包含恒元;是否满足拉定理:子群的阶数是群阶数的因子;是否包含每一元素的完整周期,是否满足封闭性
法三:若已知子群,则从子群中根据“不变子群必然由若干个完整的类组成(背)”来寻找。
这里就是由法3寻找出来的不变子群。

由于每个复元素中元素数目都相等,为4,故商群是3阶群(3个元素),由于3阶群只有一种,故商群为群
8.立方体和正八面体固有点群—O群
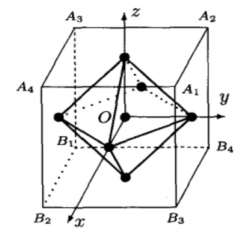

- 3个四次轴、4个三次轴、6个二次轴:
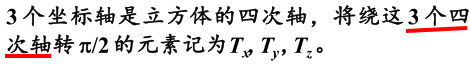

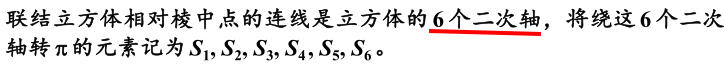
- 立方体四次轴的转动使3个四次轴等价、双向,立方体四次轴的转动使4个三次轴等价、二次轴的转动使4个三次轴双向,
比如A4B2中点与A2B4中点的连线使A3B3双向。
6个二次轴等价。
二次轴没有极性。
- 立方体的所有固有对称变换的集合构成O群,它有24个元素(类似T群的分析可以得出),恒元是一类,绕3个四次轴正、逆向转pi/2的6个元素是一类,转pi的3个元素是一类,绕4个三次轴正、逆向转动的8个元素是一类,绕6个二次轴转动的6个元素是一类,共5个类。这5个类都是自逆类。
- O群的乘法表

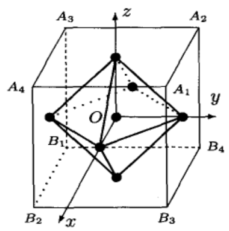
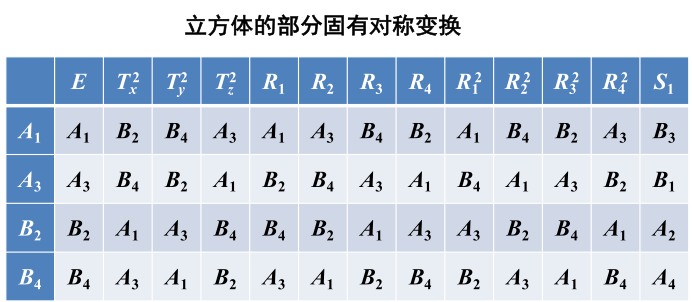
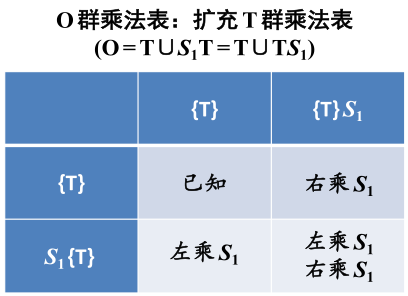
由于指数是2,所以剩下的元素可以写成

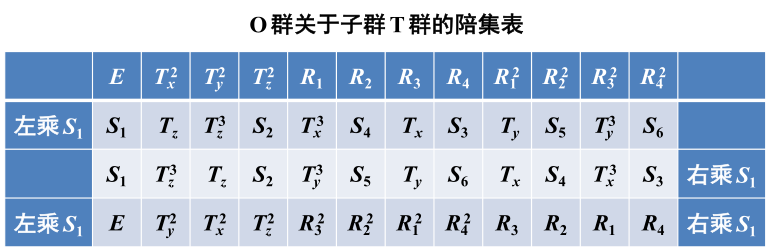
老师没讲这个表
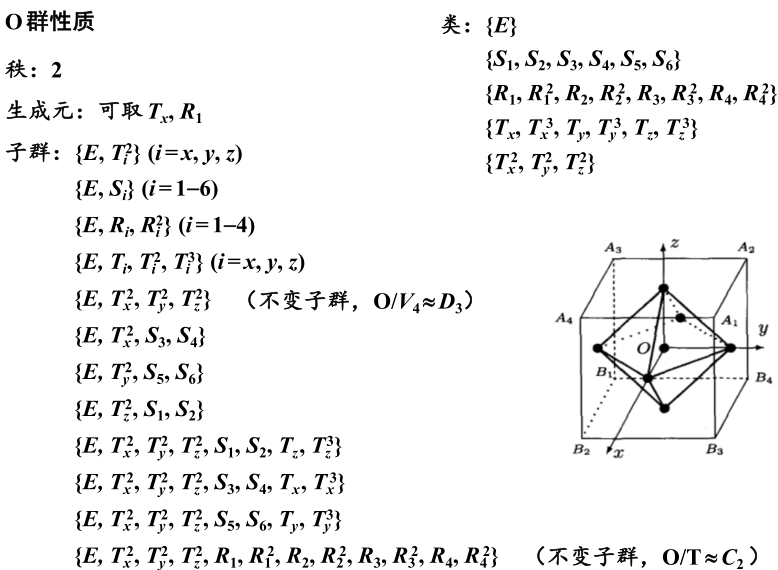
找子群:先找周期,再并起来,看是否满足封闭性。
找类:前面已经说了这5个类。
- O群的不变子群:T群[O群关于T群的商群
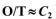 ]、
]、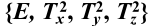 [O群关于
[O群关于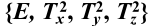 的商群
的商群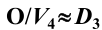 ]
]
因为T群的指数为2,商群为只有两个元素,有两个元素的群只有群。
由右上角T群的类知,因为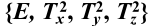 由两个完整的类组成,故它是不变子群,O群关于
由两个完整的类组成,故它是不变子群,O群关于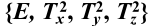 的商群有6个元素,六阶群只有两种,由前面介绍六阶群知,如果是,则必须包含6阶元素,写出商群的六个元素并能判断出没有6阶元素,故是群。
的商群有6个元素,六阶群只有两种,由前面介绍六阶群知,如果是,则必须包含6阶元素,写出商群的六个元素并能判断出没有6阶元素,故是群。
9.正十二 、 二十面体固有点 群—I 群

建立如图所示的坐标系。正二十面体和正十二面体互为对偶正多面体,有相同的固有对称变换群—I群。
- 6个五次轴、10个三次轴、15个二次轴:
正二十面体的6个相对顶点的连线是正二十面体的6个五次轴。
两个相对侧面中心的连线是正二十面体的10个三次轴。
联结正二十面体相对棱中点的连线是正二十面体的15个二次轴。 - 正二十面体五次轴的转动使6个五次轴等价、二次轴的转动使6个五次轴双向,10个三次轴等价、双向,15个二次轴等价。
- 正二十面体的所有固有对称变换的集合构成I群,它有60个元素,恒元是一类,绕6个五次轴正、逆向转2p/5的12个元素是一类,正、逆向转4p/5的12个元素是一类,绕10个三次轴正、逆向转动的20个元素是一类,绕15个二次轴转动的15个元素是一类,共5个类。这5个类都是自逆类。
- I群没有非平庸不变子群。