群论第三章 (2)(投影算符需要学,在应用于量子力学中有用,幂等元在置换群才有用,可以不学)
第章
1.5节 新表示的构成
1. 商群的不可约表示、表示的直乘、直乘群的表示
1)定理一:商群的不可约表示也是原群的不可约表示
2)定理二:有限群 的两不可约表示 和 的直乘 仍是群 的表示; 若 是一维表示,则 是群 的不可约表示
3)定理三:若有限群 等于两子群的直乘 , 则群 的不等价不可约表示都可表示为两子群 和 不等价不可约表示的直乘
a.举例:
b.“群 的不等价不可约表示都可表示为两子群 和 不等价不可约表示的直乘”的计算方法:
c.定理三的推论:
d.定理二和定理三的区分
2.分导表示和诱导表示
1)分导表示:知道了原群的不可约表示怎么知道子群的不可约表示
例:
2)诱导表示:知道了子群的不可约表示怎么知道原群的不可约表示(群论第15节课1小时32分讲了诱导表示)
分导表示和诱导表示的区分
3)费罗贝尼乌斯(Frobenius)定理:
1.2节 有限群不可约表示的特征标表(老师说这一节“特征标表”一定会考,故这几个例子一定要自己看看,但考试比我们讲得更简单,考试只是在特征标表中去掉几个空,不用分析其不变子群,只需要根据每一行正交归一,每一列正交归一即可填空。作业题中没有这样的题,作业题中特征标那题不是填空,而且复杂,应该不考)
1.有限群不可约表示的特征标表
2.如何确立有限群不可约表示的特征标表
1)一般原则
(1)有限群不等价不可约表示维数的平方和等于群的阶数
(2)有限群不等价不可约表示的个数等于群的类数
(3)有限群不等价不可约表示的特征标构成类空间的正交完备基,即特征标表中行是正交的,列也是正交的(背)(此原则一般在群中用,在群中一般不用,除了等,但这公式复杂,考试不会考太难,只是特征标表填空,故不记这两个公式)
2)辅助方法和技巧
a.任何群都有恒等表示,每个元素在恒等表示中的特征标都是1
b.恒元在 某 一不可约表示中的特征标等于 该 不可约表示的维数
c.新表示的构成一节中定理一:商群的不可约表示也是原群的不可约表示 (而且是 非真实表示 )(背,重要)
d.新表示的构成一节中定理二的一部分:群的一维非恒等表示与高维不可约表示直乘,仍是群的不可约表示(背,重要)
e.新表示的构成一节中定理三:若群等于两子群的直乘,则其所有不等价不可约表示都由两子群的不等价不可约表示的直乘给出(背,重要)
f.阿贝尔群的不可约表示都是一维的(背,重要)(一维表示的特征标就是表示矩阵)
g.除恒等表示外,有限群任意一不可约表示的特征标对群元素求和等于零(背,重要)。
h.有限群表示中,自逆类的特征标为实数,相逆类的特征标互为复共轭(背)
i.有限群不可约的非自共轭表示与其复共轭表示(不可约)成对出现,特征标互为复共轭;不可约自共轭表示的特征标为实数(不用记,用不到)
j.不可约表示的充要条件:特征标模方对群元素求和等于g(背,重要)
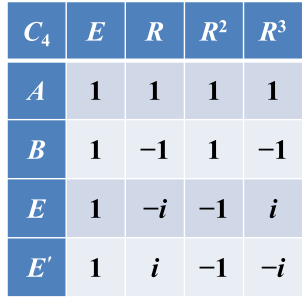
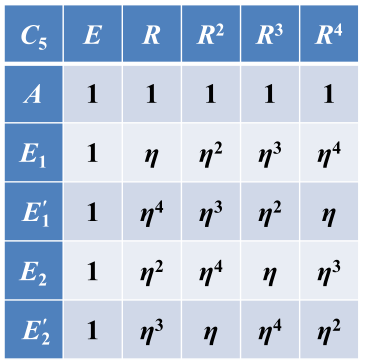
3.循环群不可约表示的特征标表
1)循环群中元素R在N个不等价不可约表示中的表示矩阵分别为(背):
2)例:循环群:公式法最好
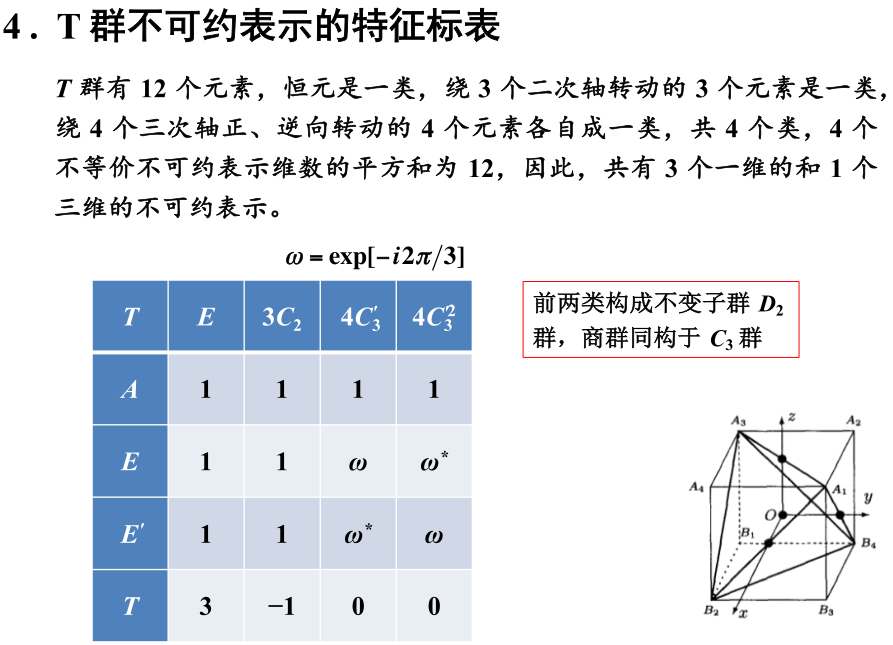
4. 群的不可约表示的特征标表
1)
2)
3)
4)(难)
5)
1.3节 投影算符和有限群群代数的分解
1. 投影算符
1)定义
投影算符的本质(背):
2)性质1:设 为任意函数, 若 非零,则为 这个第个不可约表示的第 列的函数(背,重要)。
3)性质2:
4)性质3
判断任一函数是否属于 某不可约表示确定 列函数的充要条件
现在考虑性质1中的前提条件何时成立:即什么情况能使得 非零:
例题
讨论性质3:
讨论性质1:
1.5节 新表示的构成
根据

求C2群所有不等价不可约表示:C2群有两个类,因为有限群不等价不可约表示的个数等于群的类数,故C2群有两个不等价不可约表示,因为不等价不可约表示维数的平方和等于群的阶数,故,故x=1,y=1,故C2群{E,R}有两个一维的不等价不可约表示,因为任何一个群都有一个恒等表示(表示矩阵:1,1),故其还有一个一维非恒等表示(类似求D3群的一维非恒等表示的方法可以得到,表示矩阵:1,-1)。现在知道了C2群的不等价不可约表示,怎么知道D3的不等价不可约表示?
知道了群的一部分表示怎么构造其他表示,知道了阶数小一点的群的表示,怎么知道阶数大一点的群的表示。这就是“新表示的构成”一节的内容。
1. 商群的不可约表示、表示的直乘、直乘群的表示
1)定理一:商群的不可约表示也是原群的不可约表示
定理一的例子:例 群关于不变子群 的 商群 的两个一维不等价不可约表示均为 群的不可约表示:

定理一证明:
证明: 商群 G/H 和群 同态,
显然商群 的任一表示是群 的非 真实表示
将群 的阶记为 , 不变子群 的阶记为 , 则商群 的阶为
若商群 的某一表示是不可约的,则
(这是根据正交定理推论5,有限群表示为不可约表示的充要条件。
)
对例子验证上面的公式:

对于群 来说,判断此不可约表示是否是原群的不可约表示:不可约表示的充要条件:特征标模方对群元素求和是否等于群的阶数:
又因为

故
故得证,商群 G/H 的该不可约表示也是原群 的不可约表示。
2)定理二:有限群 的两不可约表示 和 的直乘 仍是群 的表示; 若 是一维表示,则 是群 的不可约表示
两个表示直乘时,特征标是相乘,因为矩阵直乘是将后面的矩阵乘到前面矩阵的每个元素上,故特征标是相乘。
1.矩阵的直乘:其实就是量子力学的直积,第一章讲了

根据矩阵乘法和直乘的方法可以证明:
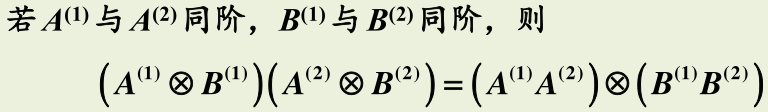
2.定理二证明:
在证明过程中用到了:任何有限群一维表示的特征标模为1。
一个结论:
有限群一维表示,其表示矩阵的模和特征标的模都是1.
证明:因为有限群的表示等价于幺正表示,有限群的一维表示可以通过相似变换化为幺正的,一维表示作相似变换,即X乘一个数再乘这个数的逆,最后会发现一维表示作相似变换后还是它自己,即相似变换后化为的这个幺正表示就是它自己,故它自己就是幺正表示,
3)定理三:若有限群 等于两子群的直乘 , 则群 的不等价不可约表示都可表示为两子群 和 不等价不可约表示的直乘
直乘群复习:(见第二章)

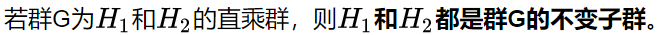


a.举例:
此定理说有限群 的两不可约表示 和 的直乘 ,比如C6群是![]() (一个C2,一个C3)的直乘,比如V4群是
(一个C2,一个C3)的直乘,比如V4群是![]() (两个C2)的直乘,根据此定理:群G的不等价不可约表示都可表示为两子群H1和H2不等价不可约表示的直乘,
(两个C2)的直乘,根据此定理:群G的不等价不可约表示都可表示为两子群H1和H2不等价不可约表示的直乘,
因为已知C2的两个不可约表示(1,1和1,-1),故根据此定理三可以求出V4的所有不等价不可约表示,一个C2有两个不等价不可约表示,两个C2直乘刚好有4个不等价不可约表示.(5)
V4群是4阶阿贝尔群,阿贝尔群的每个元素自成一类,故有4个类,
因为有限群不等价不可约表示的个数等于群的类数,故V4群有4个不等价不可约表示,
又因为有限群不等价不可约表示维数的平方和等于群的阶数,,故,故只能有4个一维不等价不可约表示,(6)
(6)这个结论与结论(5)相同,故这验证了这个定理三的正确性。
b.“群 的不等价不可约表示都可表示为两子群 和 不等价不可约表示的直乘”的计算方法:
对V4群:

定理三证明(没时间,算了,第47分):


c.定理三的推论:
直乘群类的个数等于两子群类的个数的乘积。
证明:根据定理三知,子群 和 的所有不等价不可约表示的直乘穷尽了直乘群 的所有不等价不可约表示,又因为有限群不等价不可约表示的个数等于群的类数,故根据“b.“群 的不等价不可约表示都可表示为两子群 和 不等价不可约表示的直乘”的计算方法”知道,直乘得到的表示的个数等于每个表示的个数的乘积,故直乘群类的个数等于两子群类的个数的乘积。得证。
d.定理二和定理三的区分
定理二:有限群 的两不可约表示 和 的直乘 仍是群 的表示; 若 是一维表示,则 是群 的不可约表示
定理二说的是,同一个群有两个表示,将这两个表示直乘起来,即对于群的每一个元素,将其对应的表示矩阵直乘。若参与直乘的表示有一个是一维的,则 是群 的不可约表示。
定理三:若有限群 等于两子群的直乘 , 则群 的不等价不可约表示都可表示为两子群 和 不等价不可约表示的直乘
定理三说的是,一个群是两个子群的直乘群,则它的不等价不可约表示都可表示为两子群不等价不可约表示的直乘。
2.分导表示和诱导表示
- 群 的阶为 , 它的类 中包含 个元素,它的不可约表示记为 , 维数为 , 类 中元素 在此表示的特征标记为 或
- 设 是群 的子群,阶为 , 指数为 , 左 陪集记为 , 其中 , 补上 , 即补上,因为群G可以表示为子群并上陪集并上陪集..这样的形式,故群 的任意元素可表 示为 形式(r取1到n),** 子群 的类** 中包含 个元素 的不可约表示记为 , 维数为 , 类 中元素 在此表示的特征标记为 或
1)分导表示:知道了原群的不可约表示怎么知道子群的不可约表示
把群 的不可约表示 中与子群 元素有关的表示矩阵挑出来, 构成子群 的一个表示,这个表示称为群 的不可约表示 关于子群 的分导表示,记为 。
分导表示一般是可约的,可按子群 的不可约表示 约化:
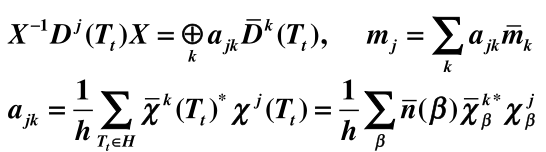
例:
D3群有一个二维不可约表示,有六个二维矩阵,D3群的子群{E,D,F}在刚才的二维表示中对应3个二维矩阵,这三个矩阵构成的矩阵群是{E,D,F}(C3群)的表示,称为分导表示。这个分导表示是可约的,可以将其向C3的不可约表示约化。
证明表示就是应证明元素对应,元素乘积对应,因为在D3中都满足元素乘积对应,故显然在{E,D,F}也满足,故得证:这三个矩阵构成的矩阵群是{E,D,F}的表示。
2)诱导表示:知道了子群的不可约表示怎么知道原群的不可约表示(群论第15节课1小时32分讲了诱导表示)
将 表示空间的基记为 , 则有
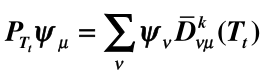
定义 , 其中
对群 的任意元素 , 将 记为 , ( 和 完全由 和 决定),则有
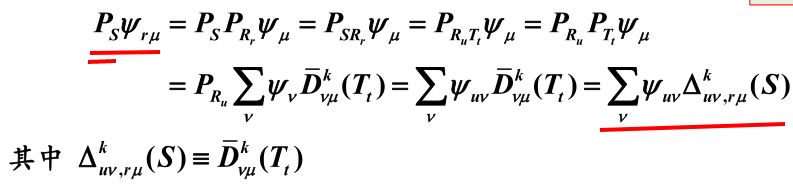
这表明 个基 架设的空间对群 保持不变,对应群 的 维 表示 , 该表示称为子群 的表示 关于群 的诱导表示
诱导表示一般是可约的,可按群 的不可约表示 约化
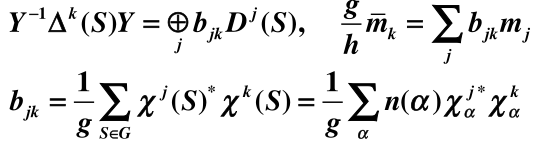
![]()
分导表示和诱导表示的区分
分导表示:从原群的不可约表示中,把关于子群的表示矩阵挑出来,构成子群的一个表示
诱导表示:有了子群的不可约表示,将表示空间扩大,它会构成群G的表示,称为诱导表示
- 怎么将表示空间扩大的?
因为
 ,将
,将 作用于子群表示空间的基,就将表示空间扩大了,扩大成
作用于子群表示空间的基,就将表示空间扩大了,扩大成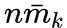 维的了,其中n是子群的指数。这样得到的是诱导表示,这个诱导表示是可约表示,应向不可约表示约化。
维的了,其中n是子群的指数。这样得到的是诱导表示,这个诱导表示是可约表示,应向不可约表示约化。
- 诱导表示的维数:子群的维数乘以子群的指数就是诱导表示的维数
3)费罗贝尼乌斯(Frobenius)定理:
有限群 的不可约表示 关于子群 的分导表示 中包含子群 的不可约表示 的重数 , 等于子群 (注意和前面求分导表示时是同一个H)的不可约表示 关于原群 的诱导表示 中包含群 的 不可约表示 的重数 , 即
不证明这个定理。只是弄懂这个定理在说什么。
有限群 的不可约表示 关于子群 的分导表示 是可约的,将其向子群的不可约表示约化,约化时不可约表示会出现几次就是重数,诱导表示同理。这个定理说的是两种重数相等。

老师说这个例题具体的东西他就不讲了。说明这个例题很可能不重要。毕竟求诱导表示的方法很复杂,很可能不考。
1.2节 有限群不可约表示的特征标表(老师说这一节“特征标表”一定会考,故这几个例子一定要自己看看,但考试比我们讲得更简单,考试只是在特征标表中去掉几个空,不用分析其不变子群,只需要根据每一行正交归一,每一列正交归一即可填空。作业题中没有这样的题,作业题中特征标那题不是填空,而且复杂,应该不考)
1.有限群不可约表示的特征标表
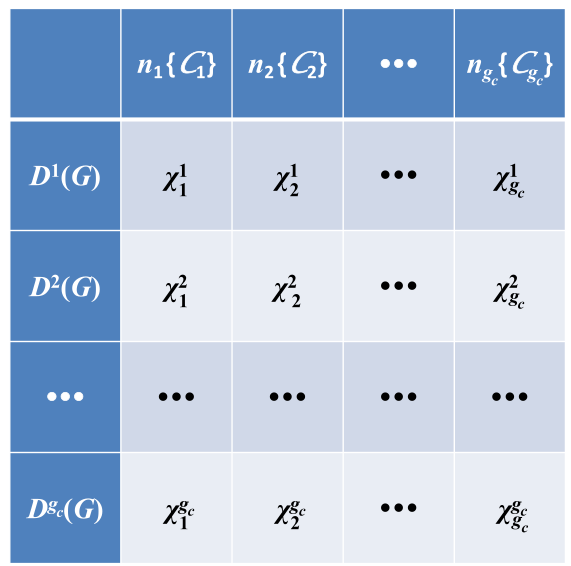
标题行:类 前标上该类元素个数
标题列: 第 个不可约表示
根据有限群不可约表示的个数等于类的个数知道,特征标表是 方阵
竖:同一类在不同表示中的特征标
横:不同的类在同一个表示中的特征标
行:不同类在同一不可约表 示中的特征标
列: 同一类在不同的不等价不可约 表示中的特征标
惯例:第一行给出恒等表示的特征标,
惯例:第一列给出恒元在各 不等价不可约表示的特征标, 即各不可约表示的维数
因为恒元的表示矩阵为单位矩阵,故其表示的特征标就是维数
2.如何确立有限群不可约表示的特征标表
1)一般原则
(1)有限群不等价不可约表示维数的平方和等于群的阶数
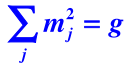
(2)有限群不等价不可约表示的个数等于群的类数
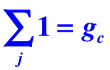
(3)有限群不等价不可约表示的特征标构成类空间的正交完备基,即特征标表中行是正交的,列也是正交的(背)(此原则一般在群中用,在群中一般不用,除了等,但这公式复杂,考试不会考太难,只是特征标表填空,故不记这两个公式)
行的正交关系
(正交性,注意其中有复共轭)
列的正交关系
(完备性,注意其中有复共轭)
2)辅助方法和技巧
a.任何群都有恒等表示,每个元素在恒等表示中的特征标都是1
这个结论需要加上一维两个字吗
b.恒元在 某 一不可约表示中的特征标等于 该 不可约表示的维数
因为恒元的表示矩阵为单位矩阵,故其表示的特征标就是维数
c.新表示的构成一节中定理一:商群的不可约表示也是原群的不可约表示 (而且是 非真实表示 )(背,重要)
d.新表示的构成一节中定理二的一部分:群的一维非恒等表示与高维不可约表示直乘,仍是群的不可约表示(背,重要)
定理二:有限群 的两不可约表示 和 的直乘 仍是群 的表示; 若 是一维表示,则 是群 的不可约表示
e.新表示的构成一节中定理三:若群等于两子群的直乘,则其所有不等价不可约表示都由两子群的不等价不可约表示的直乘给出(背,重要)
f.阿贝尔群的不可约表示都是一维的(背,重要)(一维表示的特征标就是表示矩阵)
因为设阿贝尔群有g个元素,每个元素自成一类,故g个类,根据原则(1)知,不可约表示的个数等于群的类数,故g个不可约表示。又根据原则(2)知,不可约表示维数的平方和等于群的阶数,故其不可约表示都是一维的。
g.除恒等表示外,有限群任意一不可约表示的特征标对群元素求和等于零(背,重要)。
特征标表中任何两行都正交,故也会和一维恒等表示对应的行正交,即
故得证。
h.有限群表示中,自逆类的特征标为实数,相逆类的特征标互为复共轭(背)
例子:

i.有限群不可约的非自共轭表示与其复共轭表示(不可约)成对出现,特征标互为复共轭;不可约自共轭表示的特征标为实数(不用记,用不到)
证明:先证明表示取复共轭后的特征标是原表示特征标的复共轭、一个不可约表示取复共轭后还是不可约表示:一个不可约表示D(G),取复共轭后,它一定还是一个不可约表示,因为取复共轭会使得特征标变为D(G)的特征标的复共轭,但不改变特征标的模方,之前是不可约的,特征标模方对群元素求和等于g,取复共轭后,特征标模方对群元素求和还是等于g,故其还是不可约的。
对自共轭表示,自共轭表示D(G)的表示矩阵取复共轭得到的复共轭表示与原来的表示等价,根据等价的充要条件知,特征标对应相等,又因为前面证明了复共轭表示的特征标是原来表示D(G)的特征标的复共轭,故自共轭表示的特征标为实数,或下图证明:
。
对非自共轭表示,其表示矩阵取复共轭得到的复共轭表示与原来的表示不等价,根据等价的充要条件知,特征标不会对应相等,又因为前面证明了复共轭表示的特征标是原来表示D(G)的特征标的复共轭,故有限群不可约的非自共轭表示与其复共轭表示(不可约)成对出现,特征标互为复共轭。得证。
- 有限群自逆类的个数等于不等价不可约自共轭表示的个数,相逆类的对数等于不等价不可约非自共轭表示的对数
证明复杂,没时间,省略。
不等价不可约自共轭表示的个数:等于自逆类的个数
不等价不可约非自共轭表示的对数:等于相逆类的对数
例子:


j.不可约表示的充要条件:特征标模方对群元素求和等于g(背,重要)
3.循环群不可约表示的特征标表
1)循环群中元素R在N个不等价不可约表示中的表示矩阵分别为(背):
其它元素的表示矩阵由群元素的乘积关系给出。(背)
证明: 阶循环群 是阿贝尔群
每个元素自成一类 , 共 个类, 因此有 个不等价不可约表示;
这 个不等价不可约表示维数的平方和还等于 , 因此每个不可约 表示都是一维的;即阿贝尔群的不可约表示都是一维的。
因为表示矩阵都是一维的,故![]()
因为根据表示的定义,有,故表示矩阵需满足群元素的乘积关系,有![]()
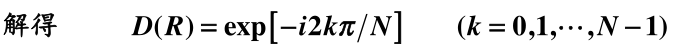
即元素 的表示矩阵有 个解,每个解代表一个不等价不可约表示,
记为 :循环群中元素R在N个不等价不可约表示中的表示矩阵分别为(背):
其它元素的表示矩阵由群元素的乘积关系给出。(背)得证。
2)例:循环群:公式法最好
根据循环群中元素R在N个不等价不可约表示中的表示矩阵公式,可以得到以下所有的循环群特征标表:
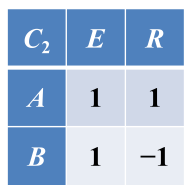
也可以根据一般原则中的三点求出以上特征标表:(2)得:2个表示,(1)得;2个一维表示,因为一定有一维恒等表示,故求出了第一行,在根据(3)特征标表中行是正交的,列也是正交的,可以求出第二行。
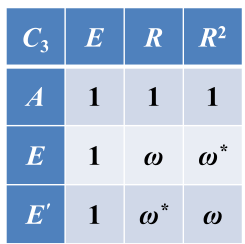
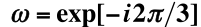
也可以根据一般原则中的三点求出以上特征标表:(2)得:3个表示,(1)得;3个一维表示,因为一定有一维恒等表示,故求出了第一行,又根据恒元对应的表示矩阵是单位矩阵求出第一列,在根据(3)特征标表中行是正交的,列也是正交的,设a,b,c,d,可以求出a,b,c,d的关系,化为只有一个自变量a,再根据“i.有限群不可约的非自共轭表示与其复共轭表示(不可约)成对出现,特征标互为复共轭;不可约自共轭表示的特征标为实数”、“j.不可约表示的充要条件:特征标模方对群元素求和等于g”可以解得复数a。但是这个方法很复杂,还是公式法最好。
![]()
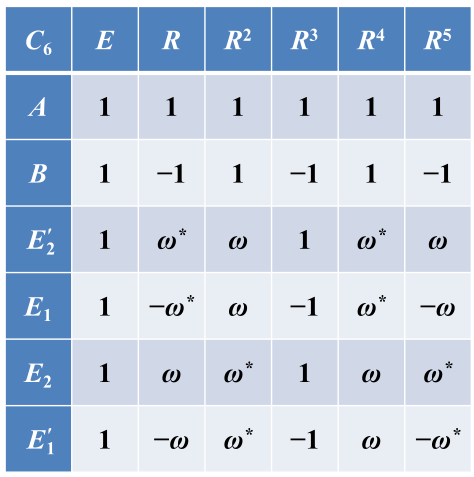
![]() 也可以得到C6
也可以得到C6
4. 群的不可约表示的特征标表
1)
群 . 群)是阿贝尔群, 有 4 个元素,一个恒元,三个二阶元素,它们各自成一类,共 4 个类,因此 4 个不 等价不可约表示都是一维的。(阿贝尔群的不可约表示都是一维的)
根据“e.新表示的构成一节中定理三:若群等于两子群的直乘,则其所有不等价不可约表示都由两子群的不等价不可约表示的直乘给出(背,重要)”和![]() 得到:
得到:
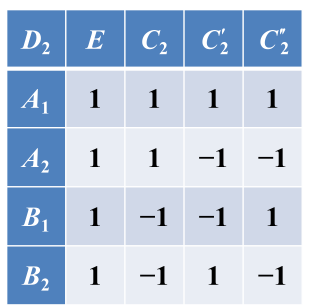

从而得到V4的特征标表。
2)
群有 6 个元素,恒元是一类,2 个三阶元素构成一类, 3 个二阶元 素构成一类, 共 3 个类, 3 个不等价不可约表示维数的平方和为 , 故该群有 2 个一维不可约表示和 1 个二维不可约表示。
法一:找不变子群,对任何一个群,是它的一个不变子群,商群是,根据“c.新表示的构成一节中定理一:商群的不可约表示也是原群的不可约表示 (而且是 非真实表示 )(背,重要)”知道,

这样得到了特征标表的前两行,
根据恒元对应的表示矩阵是单位矩阵求出第一列(注意二维表示是2),故特征标表:
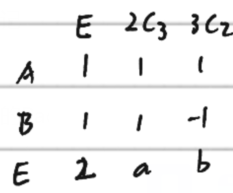
(其他方法很难解出a,b,以下方法最好)
根据“d.新表示的构成一节中定理二的一部分:群的一维非恒等表示与高维不可约表示直乘,仍是群的不可约表示(背,重要)”,根据矩阵直乘知道直乘后得到的不可约表示中![]() 对应的特征标为-b,而因为只有一个二维表示,故b=-b,解得b=0。
对应的特征标为-b,而因为只有一个二维表示,故b=-b,解得b=0。
根据“g.除恒等表示外,有限群任意一不可约表示的特征标对群元素求和等于零(背,重要)”知2+2a+3b=0,故a=-1.
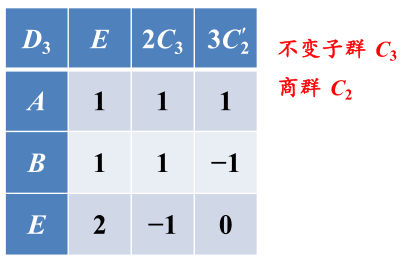
法二:像之前的例题一样求出其所有的不可约表示,再根据表示求出特征标表。
3)
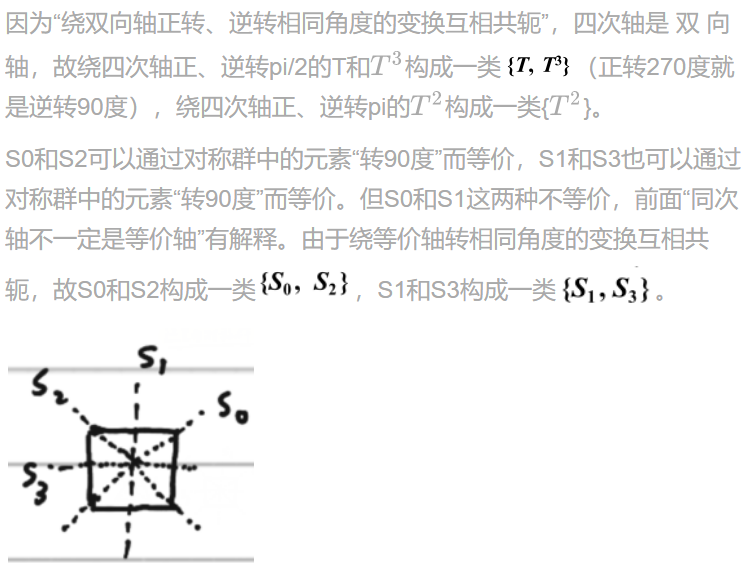
群有 8 个元素,恒元是一类,绕四次轴转动的 2 个四阶元素构成一 类, 1 个二阶元素(即绕4次轴转180度)构成一类,绕二次轴转动的 4 个二阶元素分成两类, 共 5 个类,
复习一下第二章即知道是5个类

5 个不等价不可约表示维数的平方和为 , 故该群有 4 个一 维不可约表示和 1 个二维不可约表示。
特征标表第一行都是1,第一列除了最后一行是2,其他都是1。
群有 1 个不变子群 个不变子群 , 这3个不变子群对应的商群都是 群 ; 还有 1 个不变子群 , 这个不变子群对应的商群是
根据“c.新表示的构成一节中定理一:商群的不可约表示也是原群的不可约表示 (而且是 非真实表示 )(背,重要)”知道,根据不变子群 及其商群 知道, & & 这4个元素对应1(即表示矩阵为1,因为一维,特征标为1), & 这4个元素对应-1,得到特征标表第二行。
根据不变子群 ({E, T2, S0, S2})及其商群 知, 、、对应1, 、、对应-1。
以上就是4个一维不可约表示,即得到了特征标表的前4行。
根据不变子群 ({E, T2})及其商群 知,但因为的不可约表示都是一维表示,故这样对应得不到二维表示。
设特征标表为:
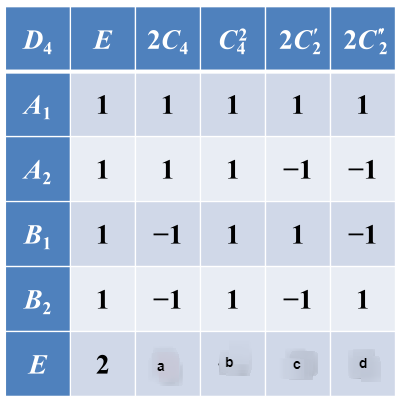
根据“d.新表示的构成一节中定理二的一部分:群的一维非恒等表示与高维不可约表示直乘,仍是群的不可约表示(背,重要)”,根据矩阵直乘知道直乘后得到的不可约表示中对应的特征标为-d,而因为只有一个二维表示,故d=-d,解得d=0。同理得a=0,c=0.
根据“g.除恒等表示外,有限群任意一不可约表示的特征标对群元素求和等于零(背,重要)”知2+b=0,故b=-2.
故特征标表: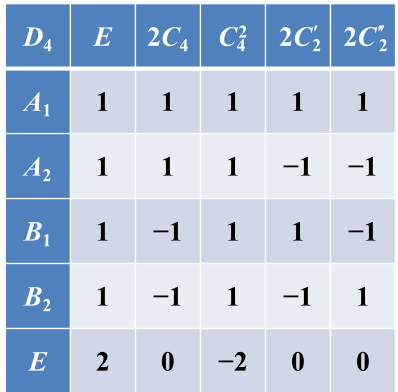
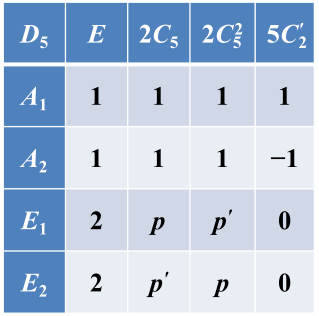
4)(难)
群有 10 个元素,恒元是一类, 4 个五阶元素分成两类,5 个二阶元 素构成一类,共 4 个类, 4 个不等价不可约表示维数的平方和为 10 , 故该群有 2 个一维不可约表示和 2 个二维不可约表示。
群有 1 个不变子群 , 商群是 群。
根据第二章中的

故第一行第一列可以得到。
设
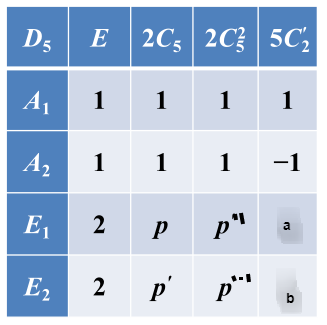
根据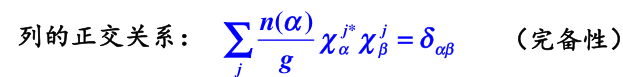

故特征标表:
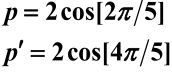
5)
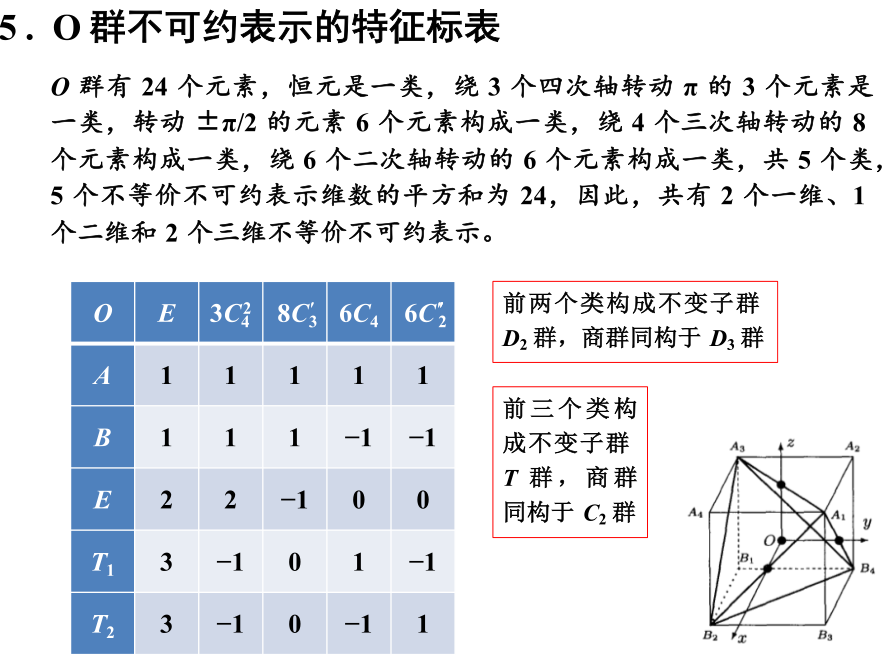
群有12 个元素,恒元是一类,绕六次轴转动的 2 个六阶元素构成一 类,2 个三阶元素构成一类, 1 个二阶元素构成一类,绕二次轴转动的 6 个二阶元素分成两类,共 6 个类, 6 个不等价不可约表示维数的平方 和为 , 故该群有 4 个一维不可约表示和 2 个二维不可约表示。
群有 1 个不变子群 个不变子群 , 商群都是 群 ; 一个不 变子群 , 商群是 群 ; 还有一个不变子群 , 商群是 群。
根据不变子群可以求出前4行。
根据中的方法得到后两行。
的另一种方法:
因为等于直乘,得到特征标表。
1.3节 投影算符和有限群群代数的分解
1. 投影算符
1)定义
设 为群 的 维不可约幺正表示,定义投影算符(背)
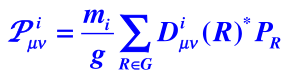
老师说,有个,故共有个这样的算符。?幺正是否有更强的限制。所以我认为这个说法是否有错误,没时间,以后再说。
共有g个线性独立的投影算符。
为什么线性独立,可能可以通过类似正交定理的推论来证明:
投影算符的本质(背):

2)性质1:设 为任意函数, 若 非零,则为 这个第个不可约表示的第 列的函数(背,重要)。
是一个算符作用于,得到的还是一个函数
证明(此证明重要):


这表明,若投影算符已知,则可从任意函数出发构造荷载不可约表示的基(背):
将投影算符作用于,得到,若其非零,则它就是这个第个不可约表示的第 列的函数(其实是荷载这个不可约表示的一个基矢量)。取遍所有的(一共有个),就得到荷载这个不可约表示的基。
得到了基之后,就可以求出这个不可约表示。但是在投影算符定义中用了![]() ,故好像是在循环,是无用功,但是这个性质的意义是:假设不知道这个表示的表示矩阵,如果有另外不一个办法,可以不根据定义而求出投影算符,则我们就可以根据此性质,从任意函数出发构造荷载不可约表示的基,得到了基之后,就可以求出这个不可约表示。这就是一个从已知的投影算符出发得到不可约表示的表示矩阵的方法。
,故好像是在循环,是无用功,但是这个性质的意义是:假设不知道这个表示的表示矩阵,如果有另外不一个办法,可以不根据定义而求出投影算符,则我们就可以根据此性质,从任意函数出发构造荷载不可约表示的基,得到了基之后,就可以求出这个不可约表示。这就是一个从已知的投影算符出发得到不可约表示的表示矩阵的方法。
在置换群一章我们就是这样从杨算符出发求表示。
3)性质2:
若 属于不可约表示 列的函数,即
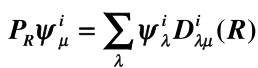
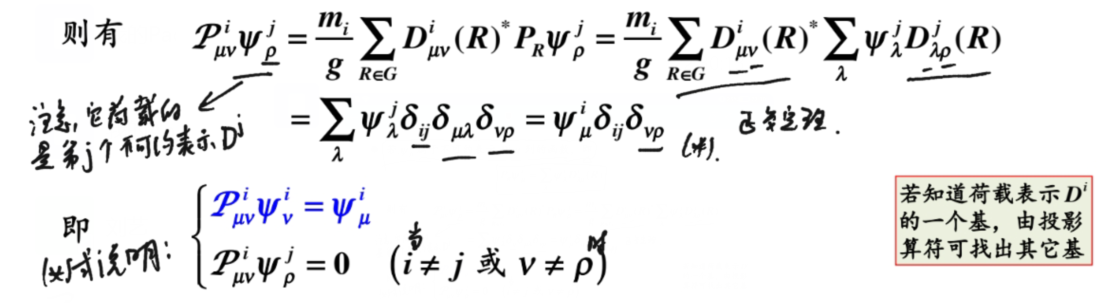
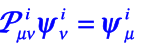 的含义(背,重要):投影算符作用在属于第个不可约表示的第 列的函数时,得到的是属于第个不可约表示的第 列的函数。
的含义(背,重要):投影算符作用在属于第个不可约表示的第 列的函数时,得到的是属于第个不可约表示的第 列的函数。
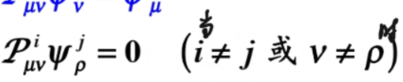 的含义:
的含义:
投影算符作用于只要不是(属于第i这个不可约表示第列的这个函数)时,结果都是0.
4)性质3
将任意函数ψ按不可约表示的基函数展开
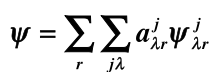
展开成属于第j这个不可约表示第列的函数,展开系数是,如果是重表示,用r来标记是哪个重表示。
例

根据性质2知道:
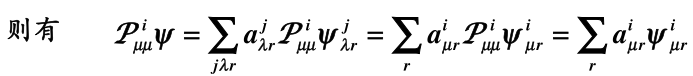
最右边的r是标记重表示。(为什么这里有重表示?重表示不是就在系数就行吗?没时间,以后再说)
这表明, 将任意函数中属于第个不可约表示的第 列的分量投影出来并将其它成分消除掉
这就是投影算符这个名字的来源
判断任一函数是否属于 某不可约表示确定 列函数的充要条件

现在考虑性质1中的前提条件何时成立:即什么情况能使得 非零:
这个函数在
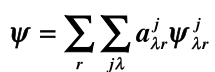 这样展开时,有属于第个不可约表示的第 列的分量时, 就非零;
这样展开时,有属于第个不可约表示的第 列的分量时, 就非零;
而当不含属于第个不可约表示的第 列的分量时, 就是零。
例题

根据投影算符公式可以写出这些投影算符。
对二维不可约幺正表示,有上面4个投影算符。
讨论性质3:
对以上所有投影算符,可以发现,其物理意义:根据性质3,因为对任意一个函数,它展开
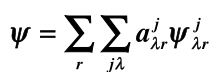 ,有4项,一项是属于一维恒等表示第一列的,一项是属于一维非恒等表示第二列的函数,还有一项属于二维不可约表示第一列的函数,还有一项属于二维不可约表示第二列的函数,而根据性质3知道,将属于一维恒等表示这一项挑出来了,将属于一维非恒等表示第二列的函数这一项挑出来了,等等,故这4个投影算符将这4项都挑出来了,故将还原了。故它们之和是单位算符。
,有4项,一项是属于一维恒等表示第一列的,一项是属于一维非恒等表示第二列的函数,还有一项属于二维不可约表示第一列的函数,还有一项属于二维不可约表示第二列的函数,而根据性质3知道,将属于一维恒等表示这一项挑出来了,将属于一维非恒等表示第二列的函数这一项挑出来了,等等,故这4个投影算符将这4项都挑出来了,故将还原了。故它们之和是单位算符。
讨论性质1:
因为可以任意取,这里取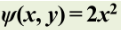 ,
,

故能知道投影算符作用于等于什么:
根据性质1:设 为任意函数, 若 非零,则为 这个第个不可约表示的第 列的函数,知道,如果投影算符作用后不等于0,得到结论:

而若将任意函数取为 ,则
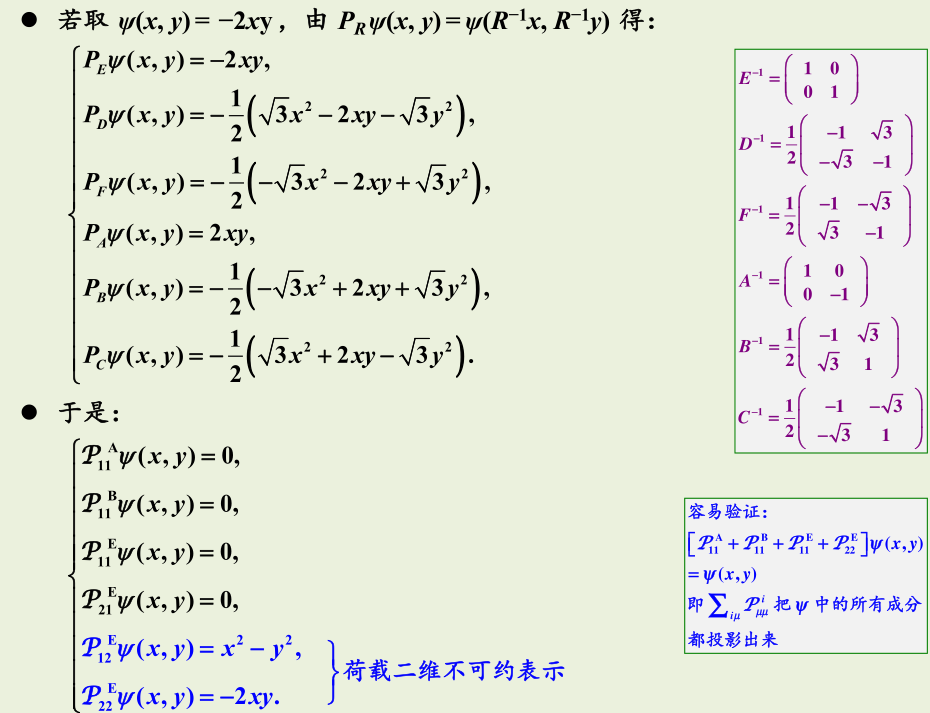
得到的荷载二维不可约表示的基的结果和刚才取 得到的荷载二维不可约表示的基相同。














【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 10年+ .NET Coder 心语,封装的思维:从隐藏、稳定开始理解其本质意义
· .NET Core 中如何实现缓存的预热?
· 从 HTTP 原因短语缺失研究 HTTP/2 和 HTTP/3 的设计差异
· AI与.NET技术实操系列:向量存储与相似性搜索在 .NET 中的实现
· 基于Microsoft.Extensions.AI核心库实现RAG应用
· 10年+ .NET Coder 心语 ── 封装的思维:从隐藏、稳定开始理解其本质意义
· 地球OL攻略 —— 某应届生求职总结
· 提示词工程——AI应用必不可少的技术
· Open-Sora 2.0 重磅开源!
· 周边上新:园子的第一款马克杯温暖上架