相互作用场论
第章
1.1节
1.回顾一下相互作用:
1)比如可以在KG场论中引入3理论。
2)4理论:
3)汤川理论:狄拉克粒子和一个自旋为零的粒子耦合
4)QED
a.QED拉氏量:
b.QED拉氏量(5)是规范不变的
c.EL方程
5)标量QED
6)杨米尔斯场论
2.哈密顿量
3.相互作用QFT的困难
4.粒子的衰变宽度、散射截面
1)S矩阵:
下面考虑庞加莱对称性(其他对称性可以类似考虑):
下面考虑内禀对称性:
考虑时间反演对称性:
考虑空间反演对称性:
1.2节 散射截面和衰变率
下面介绍运动学
4.老式微扰论/Lippman-Schwinger 方程 不考
下面开始应用(51)式:
1.1节
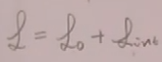
![]() :最多两阶导数
:最多两阶导数
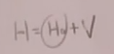
其中H_{0}=

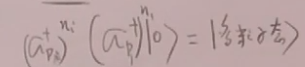
以上只是无相互作用场论。
1.回顾一下相互作用:
1)比如可以在KG场论中引入3理论。
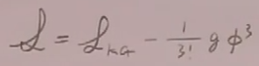
EL方程:
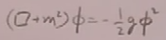
2)4理论:
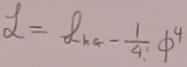
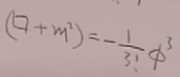
这些方程都是非线性方程。
3)汤川理论:狄拉克粒子和一个自旋为零的粒子耦合
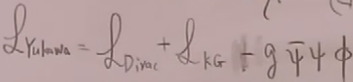
其实相互作用拉氏量也可以写成: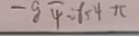
这一类都称为汤川理论。
4)QED
a.QED拉氏量:
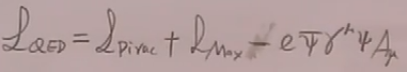
量子化电磁场时,
类比经典情况的拉氏量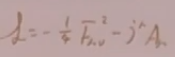 ,这是说耦合一个外源。规范不变性要求必须是一个守恒流。
,这是说耦合一个外源。规范不变性要求必须是一个守恒流。
知道:QED拉氏量中
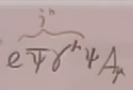 ,根据诺特定理知道,是守恒流,即
,根据诺特定理知道,是守恒流,即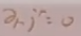 。
。
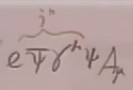 这一项就是将狄拉克场和电磁场耦合起来。
这一项就是将狄拉克场和电磁场耦合起来。
QED拉氏量等于(背):
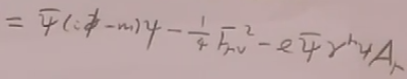
引入协变导数:![]()
其中e:电子电荷,在peskin书中,电子电荷是负的,![]()
则QED拉氏量等于:(背)
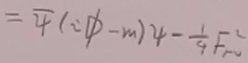 (5)
(5)
b.QED拉氏量(5)是规范不变的
U(1)规范变换(包含(6)和(7)两个公式):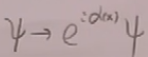 (6),其中是依赖于时空的任意一个函数,因为依赖于x,故称为是一个定域的对称性。
(6),其中是依赖于时空的任意一个函数,因为依赖于x,故称为是一个定域的对称性。
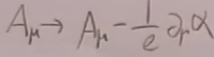 (7)(量子化电磁场一节讲了)(但是学生友好量子场论书中讲的库伦规范不一样)
(7)(量子化电磁场一节讲了)(但是学生友好量子场论书中讲的库伦规范不一样)
根据(6)、(7)得到:在U(1)规范变换下,的变换:
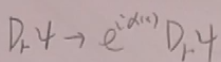 (8)
(8)
证明:
,代入(6)、(7)得到:
=
。得证。
根据(6、7、8)可以验证QED拉氏量(5)是规范不变的。
c.EL方程
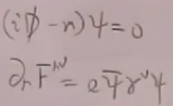
5)标量QED
前面讲的是旋量QED,旋量QED是考虑一个自旋1/2的电子和光子相互作用,但原则上还可以考虑带电的零自旋粒子,比如介子,和光子相互作用,这称为标量QED。
复KG场论:
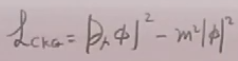
其中是一个复标量场。
将其偏导数变成协变导数即变成相互作用的理论:
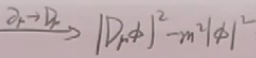
=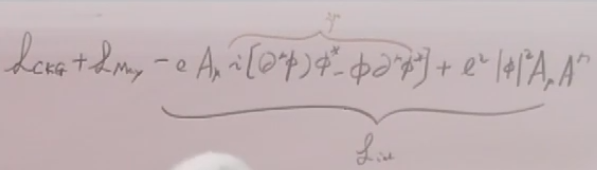
在诺特定理笔记中讲了就是复的KG场论中U(1)的诺特流(守恒流),其零分量对全空间积分就等于电荷。
标量QED比旋量QED更复杂在于:![]()
6)杨米尔斯场论
它是旋量QED的简单推广,
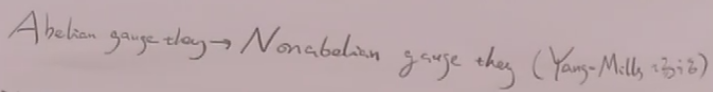
没记笔记
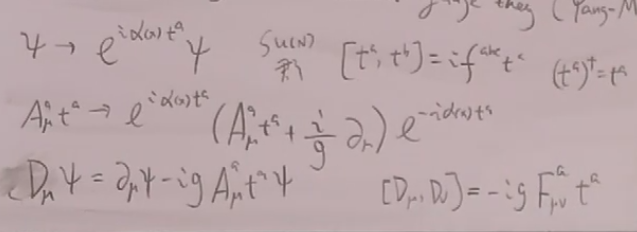
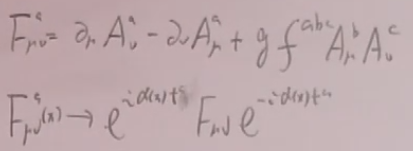
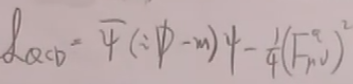
QCD的相互作用项实际上很复杂。
无质量粒子有:
零自旋的无质量粒子:这是由Goldenstone定理保证的。Goldenstone定理:一个理论如果有连续对称性的自发破缺,则它一定会出来Goldenstone玻色子,这个Goldenstone玻色子就是自旋为零的玻色子。这是非常有趣神奇的理论。
自旋为1/2的无质量粒子:
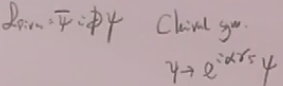
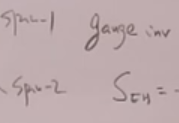
有一个定理:可重整理论所含有的最高阶的算符是量纲为4.
故不能写等。
上面说的、QED等理论都是可重整的。标准模型也是可重整的。
不可重整的含义:如果理论中含有高量纲算符,这种理论,不能将发散吸收到系数中,这种理论被认为没有预言能力。但后面发现,不可重整理论有一个有效的能标,超过这个能标,这个理论就失效了,故现在认为只要低于这个能标,这个不可重整化理论也是有预言能力的,比如手征微扰论,描述低能强相互作用。
标准模型的有效理论:是标准模型拉氏量加上高量纲算符。
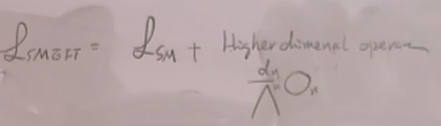
这门课是关注可重整理论。
2.哈密顿量
一般来说,若相互作用项不带导数,会发现相互作用的哈密顿量密度=-相互作用拉氏量密度:
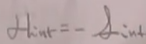 (13)
(13)
例如QED、理论中相互作用拉氏量中都没有导数耦合,故这两种情况,(13)式成立
若相互作用带导数,会有点麻烦,共轭动量会和自由场的不太一样
哈密顿量:
因为拉氏量是定域的,故一般哈密顿量也是定域的,但一个例外是考虑QED,
其中
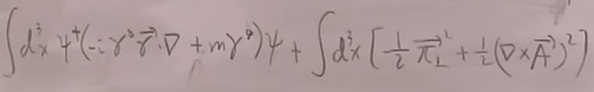
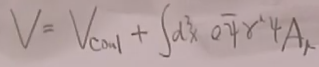
其中V的第一项是瞬时的超距的库伦相互作用,这一项不是局域的。我们希望V能写成这种形式: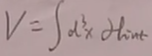 ,H_int是一个只有局域的场的乘积。故因为第一项不是局域的,所以你可能会有点担心,但其实问题不大,因为费曼传播子在库伦规范下,第一项库伦项会被去掉,而V中的第二项
,H_int是一个只有局域的场的乘积。故因为第一项不是局域的,所以你可能会有点担心,但其实问题不大,因为费曼传播子在库伦规范下,第一项库伦项会被去掉,而V中的第二项![]() 还是局域的。
还是局域的。
3.相互作用QFT的困难
考虑理论(以前说过这个理论不好,它没有稳定的基态),其共轭动量:
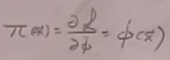
根据(13)知道哈密顿量密度: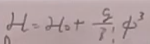
等时量子化条件:
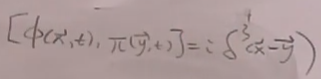
在t=0,薛定谔绘景,平面波展开:
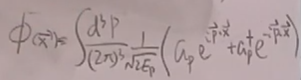 (16)
(16)
为了满足正则量子化条件,会发现:
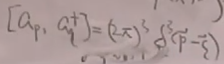 ,这和自由场论中的一样。
,这和自由场论中的一样。
复杂性出现在相互作用:
自由哈密顿量:
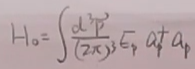
相互作用项:(L=T-V,H=T+V,故下面的V确实是这个形式)
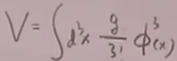 ,代入(16),得到:V=
,代入(16),得到:V=
 (19)
(19)
其中:
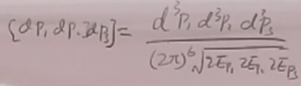
从V中可以看出只含义一个动量守恒的函数。
可以证明:

这个的后果就是:相互作用理论的真空往往不同于自由理论的真空

湮灭算符是湮灭自由理论的真空,不一定湮灭相互作用理论的真空: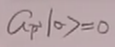 、
、 。
。
因为含相互作用项的哈密顿量含有非线性项,故很难将哈密顿量对角化。故将哈密顿量的本征态、能级求出来是一个非常困难的事情。
另外在海森堡绘景下,自由场论时,

根据对易关系,以前算过,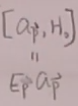 ,故
,故
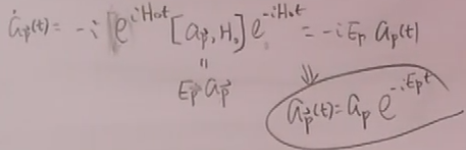 。
。
但若在有相互作用的情况,
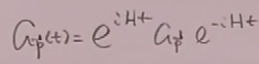
类似前面自由场的过程,得到:
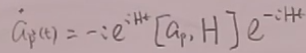
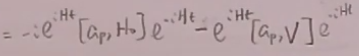 (26)
(26)
根据(19)得到:
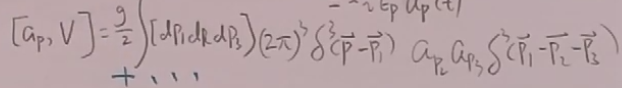
故根据(26)得到:
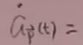
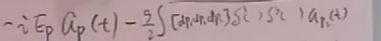
这是非线性方程,很难解,故在海森堡绘景下,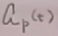 的解析表达式很复杂,解不出。海森堡绘景下的场算符也很复杂解不出。
的解析表达式很复杂,解不出。海森堡绘景下的场算符也很复杂解不出。
但有数值解法,在真实的真空下的海森堡绘景的算符构造的两点关联函数:![]()
路径积分:
=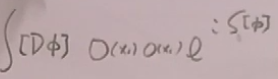 ,进行wick转动,就是将时间延拓到虚时间,
,进行wick转动,就是将时间延拓到虚时间,
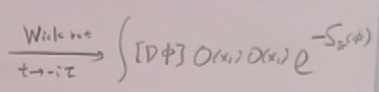
会发现,取任何实数时,指数因子是压低的,是连续的,无法算,故wilson用时空离散化,这样泛函积分就能积出来关联函数。这就是格点量子场论。蒙特卡洛方法。取连续极限:a趋于0的极限。这是非微扰的方法。
另一种微扰论方法:
![]() ,
,![]()
若相互作用部分远远小于自由部分,微扰论。若![]() 中
中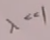 ,则可以进行小量展开,微扰论。
,则可以进行小量展开,微扰论。
但特别注意微扰论有适用范围,必须论证耦合常数很小。
比如: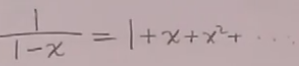

QED就是用这种方法,而且有效。
而对于强相互作用QCD,在能量低时,QCD的耦合常数是很大的,不能用微扰论,比如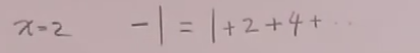
这门课是用费曼图来微扰论计算。
4.粒子的衰变宽度、散射截面
粒子的衰变宽度、散射截面这两个是可观测量,与这两个可观测量项联系的是S矩阵。
1)S矩阵:
例如:
考虑两个束流,从t=-无穷,若考虑这束粒子的动量确定,则根据不确定原理,粒子的位置不能确定,弥漫在整个空间,故不能用平面波来描述束流。故应看成高斯波包,是很多平面波的叠加,最后取一个波包宽度为0的极限,原则上可以得到正确的结论。
初态是两个离得非常非常远的电子和正电子的束流,因为离得很远,故不考虑它们间的相互作用,故好像是自由粒子一样。两个束流匀速趋近,在t=0时,碰撞(两个电子碰撞时间很短,大约是10的负十几次方),发生了极其复杂的量子反应。若某种反应产生了一个粒子对,在t=无穷时,这两个粒子分离了,又变成两个类似独立的粒子。
在对撞点有子探测器,是在对撞点探测子的能量和动量。我们不能在t=0时知道发生了什么,但是可以知道在t=无穷时在某个动量方向的几率。
对in态:

在海森堡绘景,虽然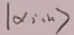 不含时,但是包含了态矢量的所有时空历史。
不含时,但是包含了态矢量的所有时空历史。
对out态:和前面类似。
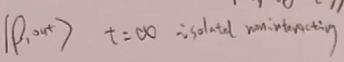
S矩阵定义为:
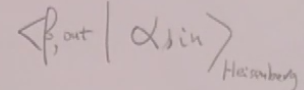 (这是定义在海森堡绘景上,海森堡绘景是态不随时间时间变化,而是算符变化)
(这是定义在海森堡绘景上,海森堡绘景是态不随时间时间变化,而是算符变化)
这是海森堡定义的。
in态和out态是完整的哈密顿量的本征态:
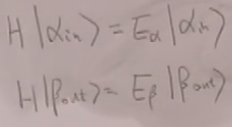 (29)
(29)
指的是在t等于正无穷时,态看起来的渐进行为是。如果将时间往前追溯,其实碰撞后的末态非常复杂。故这个S矩阵是一个几率振幅,根据量子力学的普遍物理诠释知道,
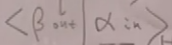 ,是末态正好是的几率振幅。(量子力学新讲有解释)
,是末态正好是的几率振幅。(量子力学新讲有解释)
引入(即没有相互作用)的本征态:
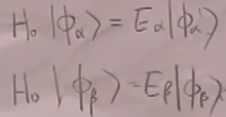 (30)
(30)
显然,(29)和(30)中的都是对应相等的,也是。
为了计算S矩阵,引入S算符:定义S算符:
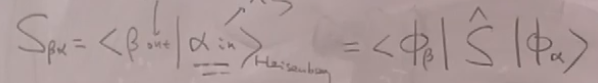
这里S算符相当于一个时间演化算符。
S矩阵元的重要性质:
- S矩阵是幺正矩阵
证明:
完备性条件:
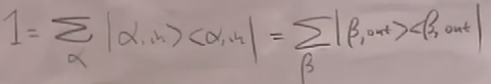
求和是对所有可能的能量本征态求和。
正交条件: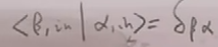
有:
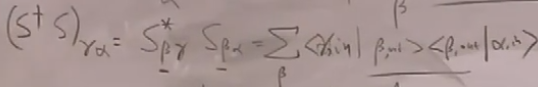
又利用一次完备性条件,故
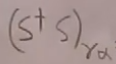 =
=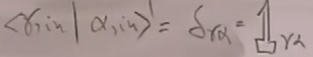 ,这就证明了S矩阵元是幺正的;
,这就证明了S矩阵元是幺正的;
类似地,可以证明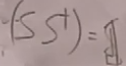 。
。
S矩阵元是幺正的物理意义:几率守恒,老师没说清楚,见量子力学新讲。
- S矩阵体现了所有的对称性(不管是内禀的还是时空还是其他对称性)。以下内容大部分来自温伯格书,应该不考
下面考虑庞加莱对称性(其他对称性可以类似考虑):
![]()
其中![]() =1
=1
其中![]() 是庞加莱变换算符,a平移,是洛伦兹变换。U是线性幺正算符,故:
是庞加莱变换算符,a平移,是洛伦兹变换。U是线性幺正算符,故:
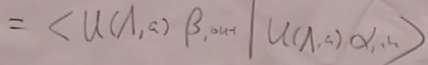
取,即考虑时空平移算符,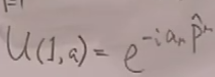
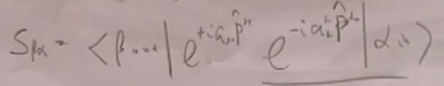
设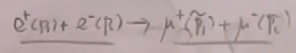
故
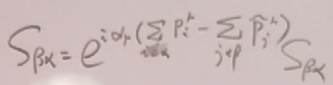
这就是说,根据时空平移不变性,自动得到了时空平移不变性的要求:必须有4动量守恒,这显然可以推广到初态有任意个粒子,末态有任意个粒子。
S矩阵元可以写成(这是定义出来的,原因见peskin104页,高量也有证明):
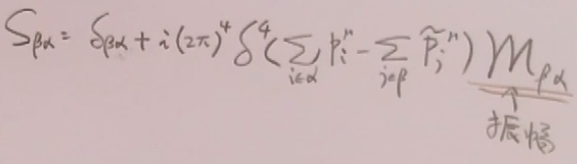
其中m称为不变振幅。所有动力学都是在不变振幅中。其中是体现了时空平移不变性。
量子场论是提供了一种框架,保证S矩阵元是洛伦兹不变。
考虑反应:
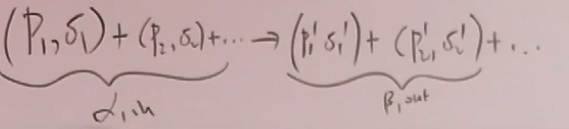
S矩阵元:
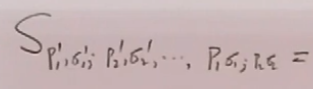
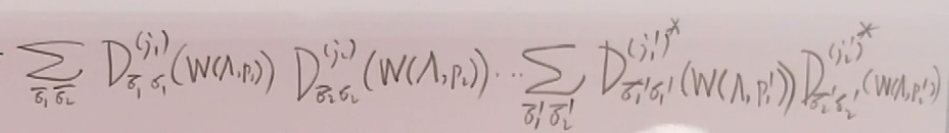
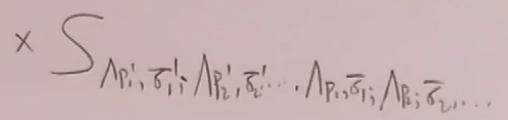
其中W是小群;D(w)是小群的表示矩阵;![]() ;
;
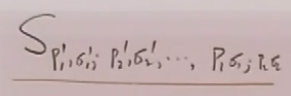 是变换前的S矩阵元;
是变换前的S矩阵元;
![]() 是洛伦兹变换后的S矩阵元,
是洛伦兹变换后的S矩阵元,
S矩阵元具有洛伦兹不变性,并不是说它在洛伦兹变换下不变,而是在洛伦兹变换下,它会变成![]() 。
。
下面考虑内禀对称性:
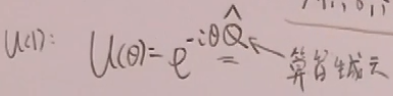
在U(1)变换下,S矩阵元的变化:
![]() =
=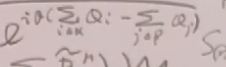
因为相位因子是任意的,要求相等的话,必须要求初态的电荷的荷等于末态的电荷的荷。故这就是导出了电荷守恒。
类似地可以验证其他对称性。
考虑时间反演对称性:
注意时间反演是反线性算符。时间反演不变对S矩阵元的要求:
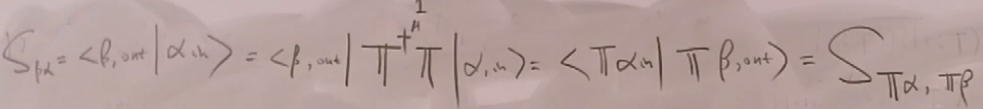
考虑空间反演对称性:
![]()
![]()
其中: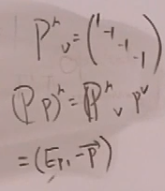 。
。
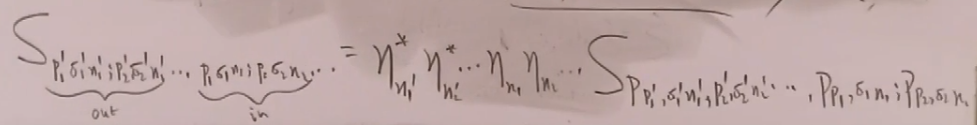
例:衰变:

可以确认内禀宇称。
1.2节 散射截面和衰变率
令![]()
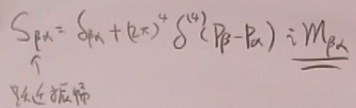
高量的散射理论中有类似的公式
![]()
而第一项平庸,不关心,舍去:
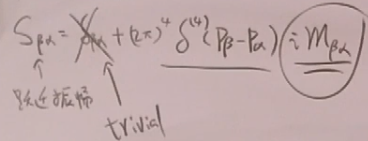
故:
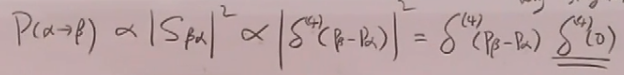
因为第一个delta函数已经强制了,故第二个delta函数中是0.
严格地处理散射问题:必须采用波包的方法。peskin书就是这个方法。
温伯格书是另一个方法:考虑将系统放在大的盒子中,

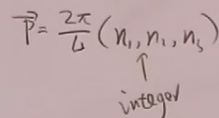 ,故
,故
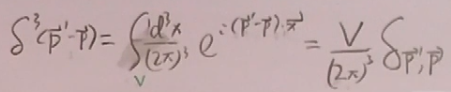
以前: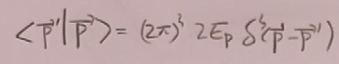
现在引入盒子中的平面波态:
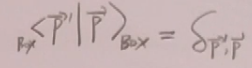
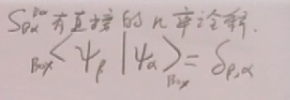
可以证明: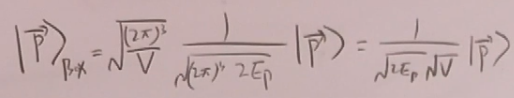
对于多个无相互作用粒子的态:

多粒子态:
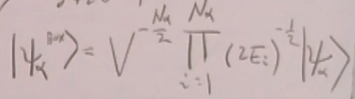
故S矩阵元:
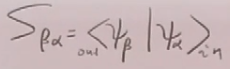
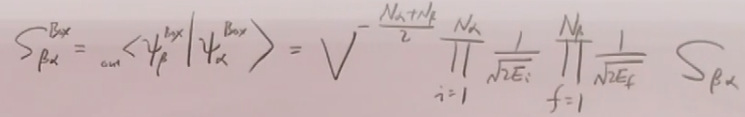
其中:
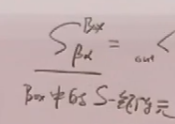 、
、
因为我们应考虑单位时间的跃迁几率,故加入时间盒子:在时间间隔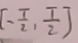 才允许打开相互作用。
才允许打开相互作用。
类似地,有:
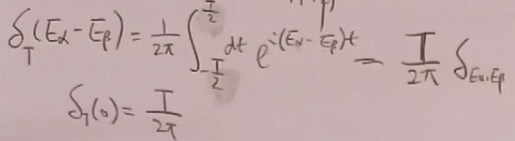
现在可以考虑跃迁几率:
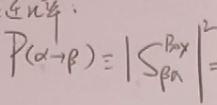
=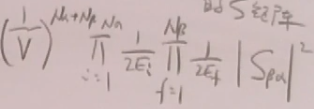 (30)
(30)
因为探测器对末态粒子动量测量的分辨率有限,故是一个相空间的间隔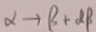 中的跃迁几率
中的跃迁几率![]() (31)
(31)
因为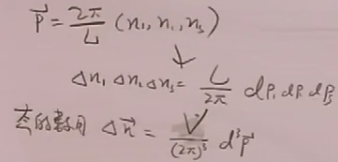
故:
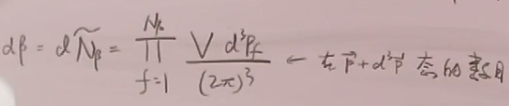 (32)
(32)
将(30)、(31)代入(32),得到跃迁概率表达式:
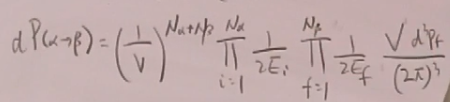
![]() =
=
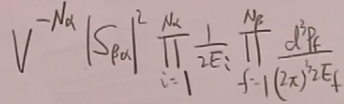 (33)
(33)
在有限空间和有限时间的处理后,S矩阵元的非平庸部分应是定义为:
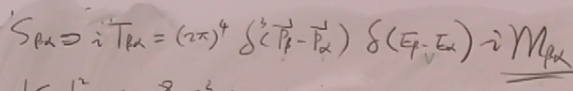
则跃迁概率:
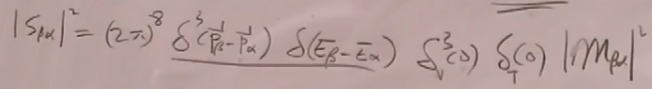
delta函数下标V和T表示的是在盒子中的. 这两个delta函数的表达式前面已经求得了,
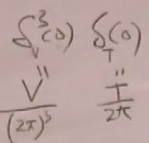 ,故代入,得到:
,故代入,得到:
![]() =
=![]() (34)
(34)
将(34)代入(33),得到跃迁几率:
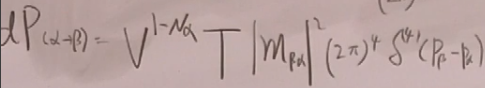
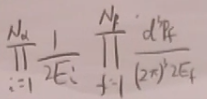
更关心跃迁速率(单位时间的跃迁几率):定义跃迁速率:
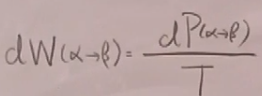 =
= (36)
(36)
其中![]() 称为洛伦兹不变的体相空间,其定义为:
称为洛伦兹不变的体相空间,其定义为:
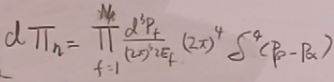 (37)
(37)
容易证明它确实是洛伦兹不变的。
以上公式是适用于初态、末态有任意多粒子,下面分情况讨论:
a.初态有一个粒子,![]() ,这代表不稳定粒子的衰变。
,这代表不稳定粒子的衰变。
根据(36)得到
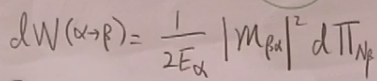
用表示dW:
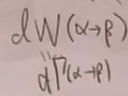 ,初态只有一个粒子的跃迁速率称为衰变宽度。
,初态只有一个粒子的跃迁速率称为衰变宽度。
(38)中的![]() 和
和![]() 都是不依赖于参考系的,而
都是不依赖于参考系的,而![]() 是4动量的零分量,它不是洛伦兹不变的,它依赖于参照系。故衰变宽度也不是洛伦兹不变的,依赖于参照系。这体现了狭义相对论的钟慢效应。穿过大气层的子,其速率接近光速,故能量很大,根据(38)知道,其衰变速率很小,故其衰变寿命很长,故可以被地球上的探测器探测到。
是4动量的零分量,它不是洛伦兹不变的,它依赖于参照系。故衰变宽度也不是洛伦兹不变的,依赖于参照系。这体现了狭义相对论的钟慢效应。穿过大气层的子,其速率接近光速,故能量很大,根据(38)知道,其衰变速率很小,故其衰变寿命很长,故可以被地球上的探测器探测到。
总宽度(之前是微分宽度,现在对末态的像空间积分,得到总宽度):
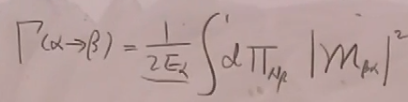
若在静止系,将入态粒子能量换成不稳定粒子的静质量即可,
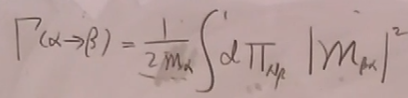
不稳定粒子在单位时间的改变率:
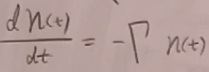
它正比于不稳定粒子的数量和总宽度。其中n(t)是不稳定粒子的数量。
可以解得: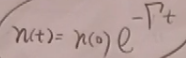 ,即不稳定粒子的数量随时间是指数衰减的。
,即不稳定粒子的数量随时间是指数衰减的。
不稳定粒子的寿命:这是算平均值。
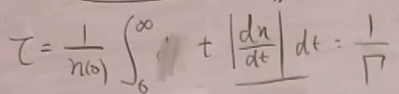
代入
即可以证明最后的结果。
不稳定粒子的平均寿命和衰变宽度成反比。
b.初态两个粒子,![]()
根据(36)得到
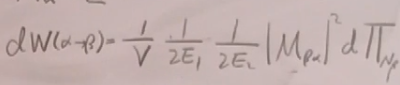 (40)
(40)
怎么处理其中的V,因为V后面要取无穷大的极限。
在经典力学中,考虑一个刚性的实心球(靶),一束束流,可以认为这个截面中是发生了碰撞。
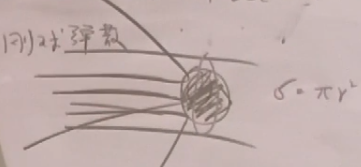
固定靶实验:
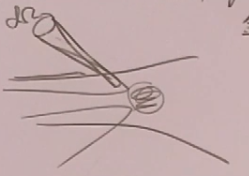
dN:事例数:多少个粒子进入立体角
通量:单位时间单位面积通过的入射的粒子数。
时间:相互作用的时间。
散射截面定义为:其量纲是面积
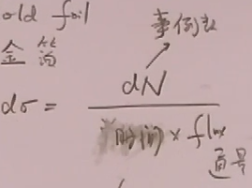
和高量中的定义不同,高量中还有
散射截面中重要单位:![]() 。对强相互作用来说,散射截面差不多刻画了一个强子的尺寸。因为强相互作用是短程相互作用。
。对强相互作用来说,散射截面差不多刻画了一个强子的尺寸。因为强相互作用是短程相互作用。
因为散射截面的定义中是事例数/(时间*通量),所以知道,实验中感兴趣的是跃迁速率除以通量,实验学家测量的是![]() 。
。
若入射粒子只有一个,box的体积为V,则其密度n=1/V. 固定靶实验中,其中v1是入射粒子的速度。故通量=
推广到相对碰撞,得到通量(流强):
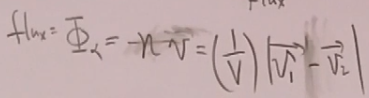 (41)
(41)
散射截面=单位时间的跃迁几率除以流强:
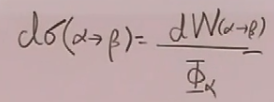 ,代入(40)和(41)得到:
,代入(40)和(41)得到:
散射截面的表达式(背):可以证明下面这个表达式是洛伦兹boost不变的。
![]()
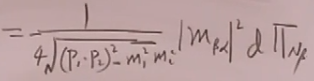 (42)
(42)
这说明这种情况,求散射截面就是应求不变振幅。
而在peskin书中的表达式:

c.入射是3个粒子,![]() ,(这种情况是在天体物理和化学中有应用)高能物理不会考虑这种情况。
,(这种情况是在天体物理和化学中有应用)高能物理不会考虑这种情况。
下面介绍运动学
对前面的b.入射两个粒子的情况,两体相空间:根据(37)知道:
![]() (43)
(43)
这个积分的计算方法:
![]() 可以写成
可以写成
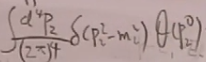
然后在(43)中先对p2积分,得,两体相空间等于:

又因为
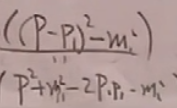 (44)
(44)
而质心系: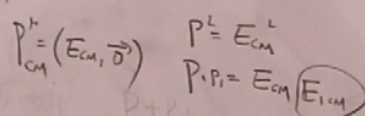 ,然后可以将(44)变成质心系,就能求出这个积分。老师说这个方法很多书都有,peskin书107。
,然后可以将(44)变成质心系,就能求出这个积分。老师说这个方法很多书都有,peskin书107。
后面就是计算不变振幅:
4.老式微扰论/Lippman-Schwinger 方程 不考
老式微扰论是对的,只是算起来比较复杂。可以帮助理解费曼微扰论。温伯格的书讲了这个老式微扰论。peskin书没讲。
散射理论:![]()
散射态:海森堡绘景中有in态和out态,它们都是完整哈密顿量的本征态,用加号代表in态,减号代表out态:![]()
定义连续态:![]() 。
。
![]()
![]()
LS方程:![]()
推导见金老师高量讲义
LS方程其实等价于薛定谔方程。
定义转移矩阵T:(这个T不是前面所的S=1+iT中的T)
![]()
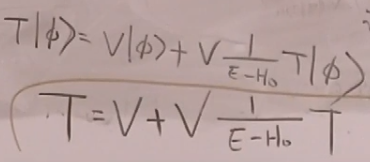
其实还应加上ie。以上两个公式的推导见金老师讲义“跃迁算符”
迭代得到: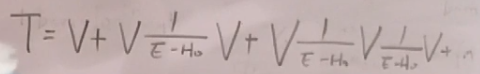 (50)
(50)
定义散射振幅:(其实散射振幅和T矩阵元之间的关系可以见周老师讲义(4.53),可知散射振幅和T矩阵元其实只相差一个常系数,故可以“认为”散射振幅就是T矩阵元,而散射截面等于散射振幅的模平方)
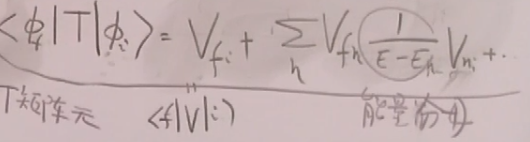 (51)
(51)
这个公式是在前一个公式中加入完备性条件![]() 得到的。
得到的。
若在以上公式中只保留第一项是一阶波恩近似(确实,见周老师高量讲义),保留二阶,则....。
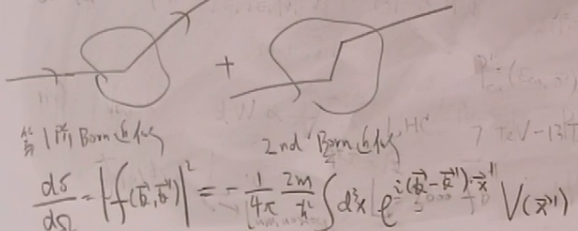
这个图可以见庄鹏飞现代量子力学讲义。
最后这个公式实际上有错误,还应该对右边进行模平方才是正确的散射截面。这是最低级波恩近似下微分散射截面的表达式,其推导见周老师高量讲义习题4.2,我写的作业答案。或者见金老师高量讲义。
下面开始应用(51)式:
考虑汤川理论:
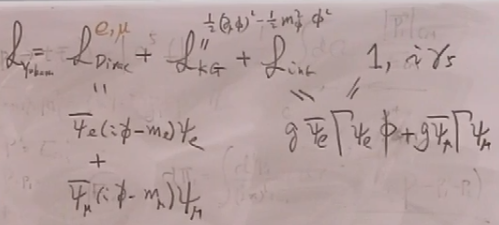
最右边少了一个,应该为
![]() ,根据很前面的定理,因为相互作用拉氏量中没有导数,故
,根据很前面的定理,因为相互作用拉氏量中没有导数,故![]()
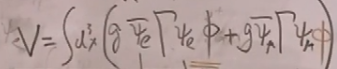
考虑电子和子的散射(通过轴子进行散射)![]() :
:
(51)中的领头阶矩阵元:
![]()
其中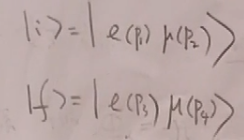 ,i和f是无相互作用的一些粒子的态。
,i和f是无相互作用的一些粒子的态。
这个矩阵元为零,因为V的表达式中都有,而中有(它们分别产生和消灭轴子),因为i和f态的表达式中都没有轴子,故再经过计算知道领头阶矩阵元为0.即![]()
具体计算推导过程省略。
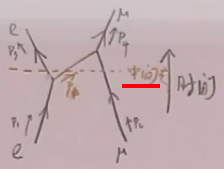
(51)推导过程中加入的中间态为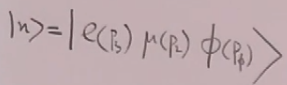
中间态有3个粒子,是轴子。
上面费曼图的物理意义:电子和子开始接近,在某个时刻电子发射了一个轴子,动量为,过了一段时间,轴子被子吸收了,且
子散射了。是在壳的粒子。图中时间较早的顶角,相互作用更早,因为这种原因,老式微扰论也称为编时微扰论。
下面计算(51)的第二项,
![]() =
=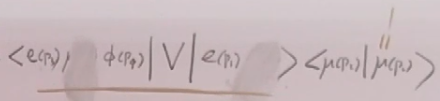 =
=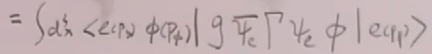
其中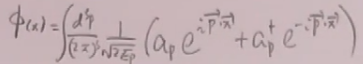 ;
;![]() =
=![]() ;
;

利用以前在自由场论讲过的
 、
、![]() 、
、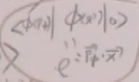 ,经过复杂的推导,得到:
,经过复杂的推导,得到:

老师说在老式微扰论中,算符都是在薛定谔绘景,t=0。
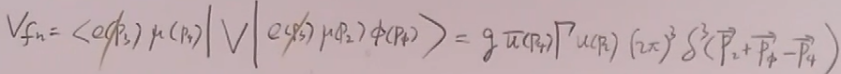
至此,(51)的第二项就求出来了。
将轴子的单位算符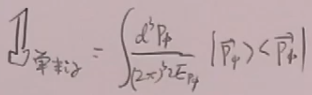 加入(51),得到:T矩阵元:
加入(51),得到:T矩阵元:
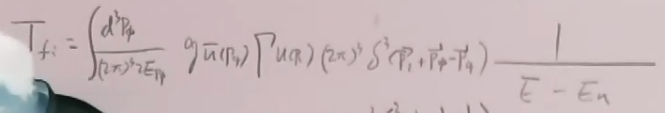
![]() (60)
(60)
E是t等于正无穷或t等于负无穷时的能量,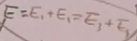 ,根据费曼图,E等于in态的两个粒子的能量,也等于out态的两个粒子的能量。而中间态能量:
,根据费曼图,E等于in态的两个粒子的能量,也等于out态的两个粒子的能量。而中间态能量: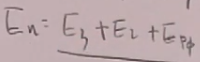 ,从此可以知道,对老式微扰论,在每个顶角,三动量守恒,但中间态能量并不等于初和末态的能量,即能量不守恒(不过初末态能量守恒),这体现了能量时间不确定关系,若中间态能量和初末态能量相差很多,这它出现的时间很短;
,从此可以知道,对老式微扰论,在每个顶角,三动量守恒,但中间态能量并不等于初和末态的能量,即能量不守恒(不过初末态能量守恒),这体现了能量时间不确定关系,若中间态能量和初末态能量相差很多,这它出现的时间很短;
故(60)变为:
![]()
![]()
还可以继续算出这个积分。没时间。
但是注意,这里根据的费曼图只是所有可能的费曼图中的一种,因为时序可以不同。
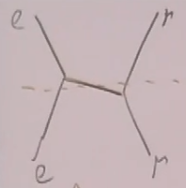
这是子先辐射一个轴子,然后电子再吸收这个轴子。可以求出这种情况的T矩阵元:
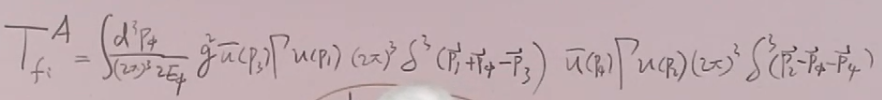

故以上两种情况的总的T矩阵元等于: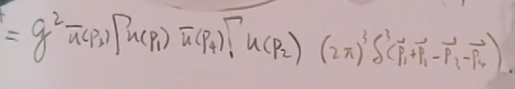
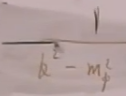 (62)
(62)
其中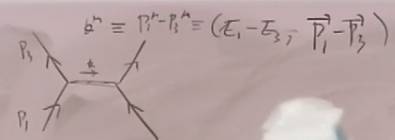 。
。
注意在以上两种情况中,顶角分别有不同的动量守恒。
(62)中的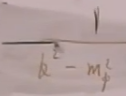 是费曼传播子。故说明以上两种情况加起来等于费曼协变微扰论的贡献。
是费曼传播子。故说明以上两种情况加起来等于费曼协变微扰论的贡献。
根据散射振幅的定义![]() 知道,不变振幅:
知道,不变振幅:
![]()
怎么推导的?不清楚,算了,以后再说,见课。写不清楚
老式微扰论图的数目很多,若费曼协变微扰论中的费曼图顶角越多,则对应的老式微扰论图特别多,复杂。但这两种微扰论都是等价的。一个有n个顶角的费曼图对应n!个老式微扰论图。
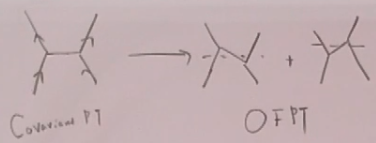
在量子力学中,波恩近似,T矩阵大致:
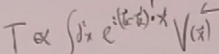
其中势V都是瞬时相互作用。
而在QFT中,两个粒子是通过交换轴子来散射。在费曼协变微扰论中,这种内线的粒子称为虚粒子,因为它是离壳的,4动量的平方不等于m的平方,即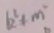 ,故称为虚粒子。而在老式微扰论中,内线的粒子是在壳的,这说明不存在超距作用,这就是通过老式微扰论得到了不存在超距作用这个重要的物理事实。当理解一些物理时,可以看看老式微扰论,也许可以减少混淆。
,故称为虚粒子。而在老式微扰论中,内线的粒子是在壳的,这说明不存在超距作用,这就是通过老式微扰论得到了不存在超距作用这个重要的物理事实。当理解一些物理时,可以看看老式微扰论,也许可以减少混淆。
费曼微扰论之所以是协变的(即洛伦兹不变的)是因为费曼传播子是洛伦兹不变的。计算来说,这种微扰论更好。

