第二章 贝里相位 最终版
关于贝里相位,**xiao di 的2010的综述**也写得很好,正确。还有周老师和陈老师的讲义也写得好。
关于量子绝热定理、绝热近似的条件:见曾谨言卷二,写得好
注:有关规范变换为什么是在波函数上乘一个e指数以及AB效应及其解释,见华中师范量子力学附件内容中贝里相位一章,写得好。
4.1 布洛赫定理和能带论
周期势场中的本征函数:

其中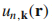 有和晶格R相同的周期:
有和晶格R相同的周期: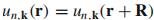 。对应的能量本征值满足
。对应的能量本征值满足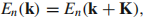 ,是倒空间的周期函数,K是倒格矢。与指标n相联系的能量连续变化,它具有波矢k,组成了一个能带,能带指标为n。对于给定的n的本征值在倒空间是周期的;所有
,是倒空间的周期函数,K是倒格矢。与指标n相联系的能量连续变化,它具有波矢k,组成了一个能带,能带指标为n。对于给定的n的本征值在倒空间是周期的;所有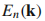 的不同的值位于倒格子的第一布里渊区。
的不同的值位于倒格子的第一布里渊区。
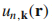 有和晶格R相同的周期:
有和晶格R相同的周期: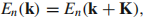 ,是倒空间的周期函数,K是倒格矢。与指标n相联系的能量连续变化,它具有波矢k,组成了一个能带,能带指标为n。对于给定的n的本征值在倒空间是周期的;所有
,是倒空间的周期函数,K是倒格矢。与指标n相联系的能量连续变化,它具有波矢k,组成了一个能带,能带指标为n。对于给定的n的本征值在倒空间是周期的;所有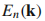 的不同的值位于倒格子的第一布里渊区。
的不同的值位于倒格子的第一布里渊区。根据泡利不相容原理,电子先填满最低的能量(热统有证明费米面),因此组成了有限密度电子系统的费米面。占据态的最高能量称为费米能级。在费米能级附近,如果一个能带部分被占据,它处于金属态。在这种情况,当一个外场加到系统中,场将使电子从平衡位置漂移,获得一个非零的总动量去组成一个电流的流动。如果能带完全填满,在价带和导带之间有能隙,它是绝缘体。在这种情况一个弱外场不能迫使电子离开占据态,而是循环。这是能带绝缘体的情况。如果能隙小于4电子伏特(粗略地),则即使在绝对零度时完全填充的满带对电导率没有贡献,但在有限温度,电子很容易从价带激发,是半导体。
4.2 贝里相位
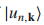 的选择不是唯一的。比如总是有
的选择不是唯一的。比如总是有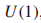 ,即一个相位不确定。
,即一个相位不确定。
在布里渊区中一组确定的相位选择被称为确定规范【2010】。对于一个时间反演不变的系统,总是存在一个连续规范穿过布里渊区。对一个时间反演破缺的具有非零的陈数的系统,不存在这样的规范,所以连续规范必须被定义在布里渊区的块中【2010,2011】。然而任何物理的可观测量必须是规范独立的。
考虑系统哈密顿量随着参数变化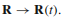 。我们对系统的循环演化很有兴趣,从
。我们对系统的循环演化很有兴趣,从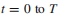 使得满足
使得满足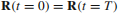 。参数在参数空间沿着闭合路径C非常慢变化。为解决这个问题,我们先引入一个瞬时正交基矢,它是从在时刻t或每个
。参数在参数空间沿着闭合路径C非常慢变化。为解决这个问题,我们先引入一个瞬时正交基矢,它是从在时刻t或每个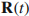 值的
值的 的瞬时本征态中获得的。
的瞬时本征态中获得的。
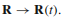 。我们对系统的循环演化很有兴趣,从
。我们对系统的循环演化很有兴趣,从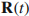 值的
值的 的瞬时本征态中获得的。
的瞬时本征态中获得的。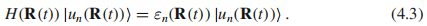
这个方程没有完全决定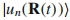 的基函数由于相位不确定性。然而我们能要求函数沿着闭合路径是光滑和单值的。这个方程也没有正确描述量子态的时间演化,相反,量子态应该被含时薛定谔方程决定:
的基函数由于相位不确定性。然而我们能要求函数沿着闭合路径是光滑和单值的。这个方程也没有正确描述量子态的时间演化,相反,量子态应该被含时薛定谔方程决定:
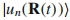 的基函数由于相位不确定性。然而我们能要求函数沿着闭合路径是光滑和单值的。这个方程也没有正确描述量子态的时间演化,相反,量子态应该被含时薛定谔方程决定:
的基函数由于相位不确定性。然而我们能要求函数沿着闭合路径是光滑和单值的。这个方程也没有正确描述量子态的时间演化,相反,量子态应该被含时薛定谔方程决定: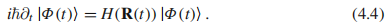
在绝热近似中[4],如果很多瞬时态中的其中一个瞬时态(通常我们选择最低能量态或基态)能和其他瞬时态清楚地分开且时间演化很慢,则系统将保持在这个瞬时本征态。在这种情况,波函数能和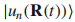 有关:
有关:
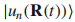 有关:
有关: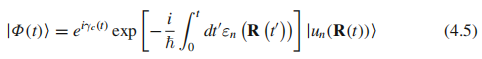
以及: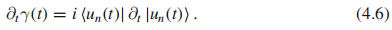
【(4.5)、(4.6)的证明:
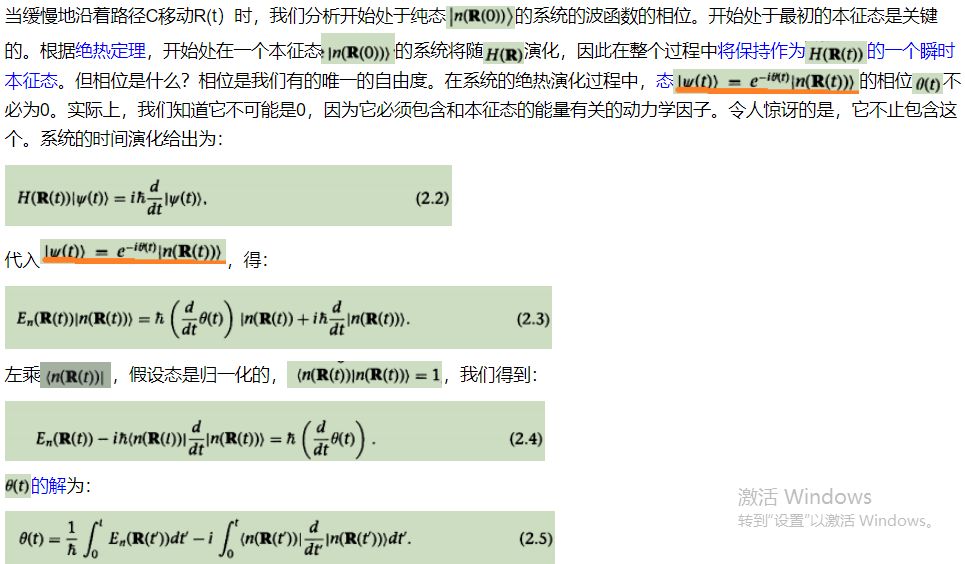

由此(2.7)可以得到沈书(4.6)】
贝里相位可以表达为路径积分:

其中贝里联络(贝里矢势):
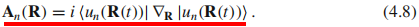
【(4.7)、(4.8)的证明:
 】
】除了由对
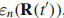 积分所确定的动力学相位,态
积分所确定的动力学相位,态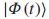 将获得一个额外的相位
将获得一个额外的相位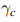 在绝热演化中。
在绝热演化中。如果我们做一个规范变换
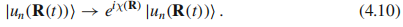
它变成:
由(4.9)知: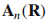 是规范依赖的。
是规范依赖的。
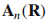 是规范依赖的。
是规范依赖的。【(4.9)证明:
 】
】因此,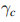 将被改变
将被改变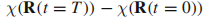 对于初始和最后的点。对于系统沿着闭合回路C的循环演化且
对于初始和最后的点。对于系统沿着闭合回路C的循环演化且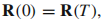 ,波函数的单值条件要求:
,波函数的单值条件要求:
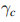 将被改变
将被改变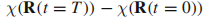 对于初始和最后的点。对于系统沿着闭合回路C的循环演化且
对于初始和最后的点。对于系统沿着闭合回路C的循环演化且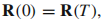 ,波函数的单值条件要求:
,波函数的单值条件要求: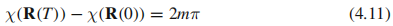
m为整数。因此对于一个闭合路径C,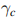 是规范独立的(因为由(4.11)知道,
是规范独立的(因为由(4.11)知道,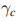 改变量是整数乘2pi,与
改变量是整数乘2pi,与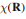 的形式无关,故贝里相位是规范不变的),现在它被称为贝里相位:
的形式无关,故贝里相位是规范不变的),现在它被称为贝里相位:
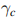 是规范独立的(因为由(4.11)知道,
是规范独立的(因为由(4.11)知道,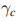 改变量是整数乘2pi,与
改变量是整数乘2pi,与
【(4.11)证明:

贝里联络明显是规范依赖的(因为由(2.11)知,不同的规范变换对应不同的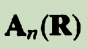 )。在一个规范变换
)。在一个规范变换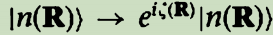 下(其中
下(其中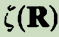 是一个光滑、单值函数)贝里联络以一种通常的方式变换:
是一个光滑、单值函数)贝里联络以一种通常的方式变换:
因此,贝里相位将被改变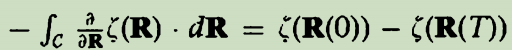 ,其中T是路径C在被完成之后的(长)时间。在贝里之前,很多人认为,通过选择规范因子
,其中T是路径C在被完成之后的(长)时间。在贝里之前,很多人认为,通过选择规范因子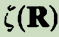 ,贝里相位能被抵消,因此贝里相位没有很大关系。这是错误的。我们考虑参数空间的闭合路径C,在长时间(T)之后,我们回到最初的参数
,贝里相位能被抵消,因此贝里相位没有很大关系。这是错误的。我们考虑参数空间的闭合路径C,在长时间(T)之后,我们回到最初的参数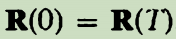 。对这样的路径,【我们选择本征态基矢为单值的】这个事实意味着当我们回到最初的参数位置,基矢必须相同:
。对这样的路径,【我们选择本征态基矢为单值的】这个事实意味着当我们回到最初的参数位置,基矢必须相同: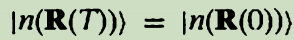 。规范变换必须保持这个性质(我的理解:【在规范变换之后也必须是单值的】这就是一个规定,(2.1)后的说明说了单值的规定),所以
。规范变换必须保持这个性质(我的理解:【在规范变换之后也必须是单值的】这就是一个规定,(2.1)后的说明说了单值的规定),所以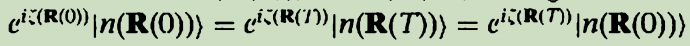 ,因此
,因此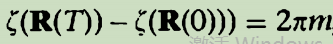 ,m为整数。因此,在一个闭合回路下,除非贝里相位是2pi乘以整数,否则贝里相位不能被抵消。】
,m为整数。因此,在一个闭合回路下,除非贝里相位是2pi乘以整数,否则贝里相位不能被抵消。】
通过斯托克斯定理,贝里相位能表达成一个面积分:
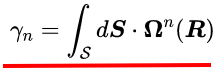
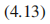
其中贝里曲率定义为:
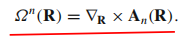
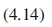
贝里曲率的分量:
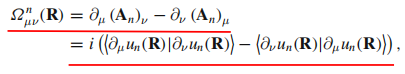
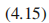
其中用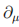 表示
表示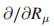 。
。
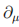 表示
表示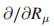 。
。【(4.14)(4.15)证明:
 】
】贝里曲率类似于电磁场中的磁场。利用基矢的完备性条件
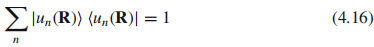
和恒等式
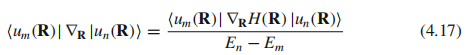
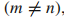 ,得到贝里曲率的另一个表达式:
,得到贝里曲率的另一个表达式:注意(4.18)中的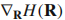 其实是应先算,应该加括号
其实是应先算,应该加括号
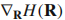 其实是应先算,应该加括号
其实是应先算,应该加括号(4.18)只有对哈密顿量求导,避免了对态求导,而且此公式不依赖于相位,计算机输出的态可以直接代入(4.18)计算。贝里曲率也是规范独立的。(这段话的证明见为知Bernevig书第二章2.2节笔记)
It is noted that the Berry curvature in (4.15) is expressed in term of one state 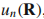 ,but that in (4.18) is expressed as a summation over all possible states. It reflects that the Berry curvature describes the global properties of a system, NOT the property of a single band.
,but that in (4.18) is expressed as a summation over all possible states. It reflects that the Berry curvature describes the global properties of a system, NOT the property of a single band.
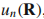 ,but that in (4.18) is expressed as a summation over all possible states. It reflects that the Berry curvature describes the global properties of a system, NOT the property of a single band.
,but that in (4.18) is expressed as a summation over all possible states. It reflects that the Berry curvature describes the global properties of a system, NOT the property of a single band.(4.18)的分量形式:
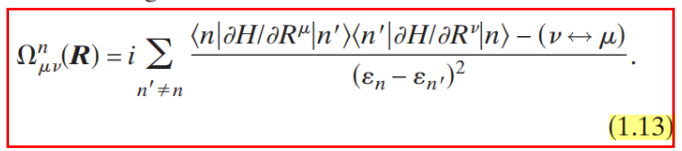 (来自xiaodi2010综述)
(来自xiaodi2010综述)另外一些公式:
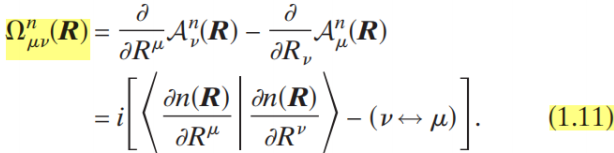
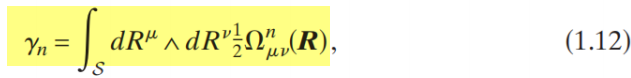
 (来自xiaodi2010综述)
(来自xiaodi2010综述)
![]()
![]()
![]()
若u_n有完备性,则:
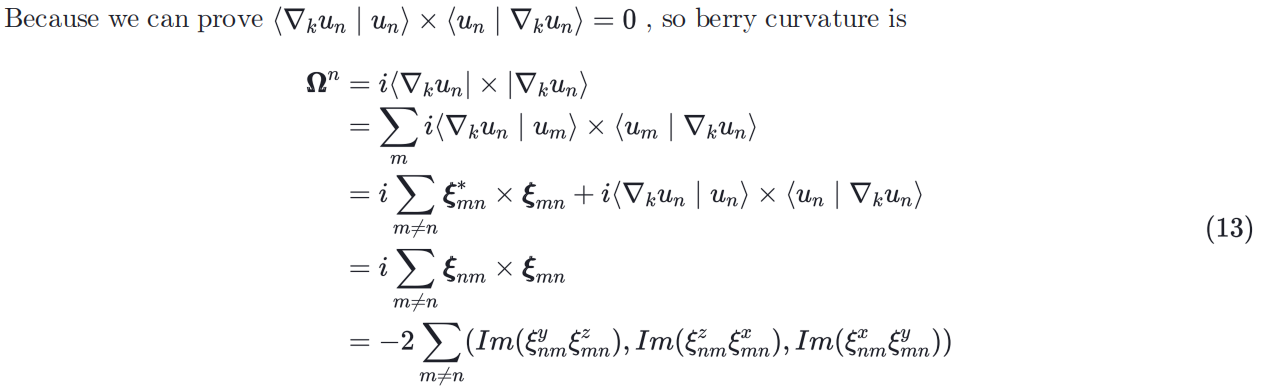
故:
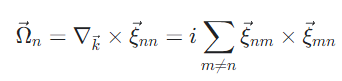
在二维情况,
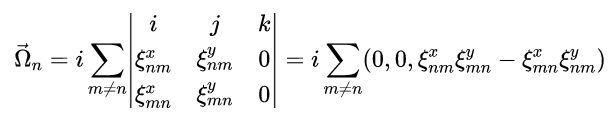
【(4.17)、(4.18)证明:
1、先证明贝里相位是实数、贝里矢势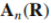 的每个分量是实数、
的每个分量是实数、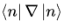 是纯虚数的证明:
是纯虚数的证明:
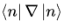 是纯虚数的证明:
是纯虚数的证明:
注意划线的地方的说法ernern有一些问题,因为它其实是一个矢量,其实意思是说这个矢量的每个分量都是复数。(由此也可知,贝里矢势、贝里联络是每个分量都是实数)

2、(4.17)的证明:引进了哈密顿量,然后类似勒朗德变换,将对态的导数变成对哈密顿量的导数。

3、最后证明(4.18):

】
考虑两能级系统作为例子。一般描述两能级系统的哈密顿量的形式:
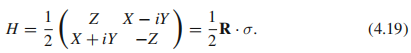
能量本征值为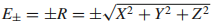 (少了一个1/2),并且两个能级在
(少了一个1/2),并且两个能级在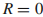 交叉。参数空间中哈密顿量的梯度:
交叉。参数空间中哈密顿量的梯度:
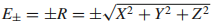 (少了一个1/2),并且两个能级在
(少了一个1/2),并且两个能级在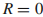 交叉。参数空间中哈密顿量的梯度:
交叉。参数空间中哈密顿量的梯度:
我们发现贝里曲率有矢量形式:
 (n为负时)
(n为负时)这个曲率能被视为一个由在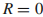 的磁单极子激发的场。将贝里曲率对包含此磁单极子的球面的积分,得:
的磁单极子激发的场。将贝里曲率对包含此磁单极子的球面的积分,得:
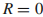 的磁单极子激发的场。将贝里曲率对包含此磁单极子的球面的积分,得:
的磁单极子激发的场。将贝里曲率对包含此磁单极子的球面的积分,得:
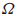 的散度有性质:
的散度有性质:
因此,一个点状“磁单极子”位于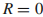 ,它激发了贝里曲率。
,它激发了贝里曲率。
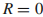 ,它激发了贝里曲率。
,它激发了贝里曲率。两能级系统的三种规范以及没有好的规范,见a short course 书39-40页。
【(4.19)、(4.20)证明:
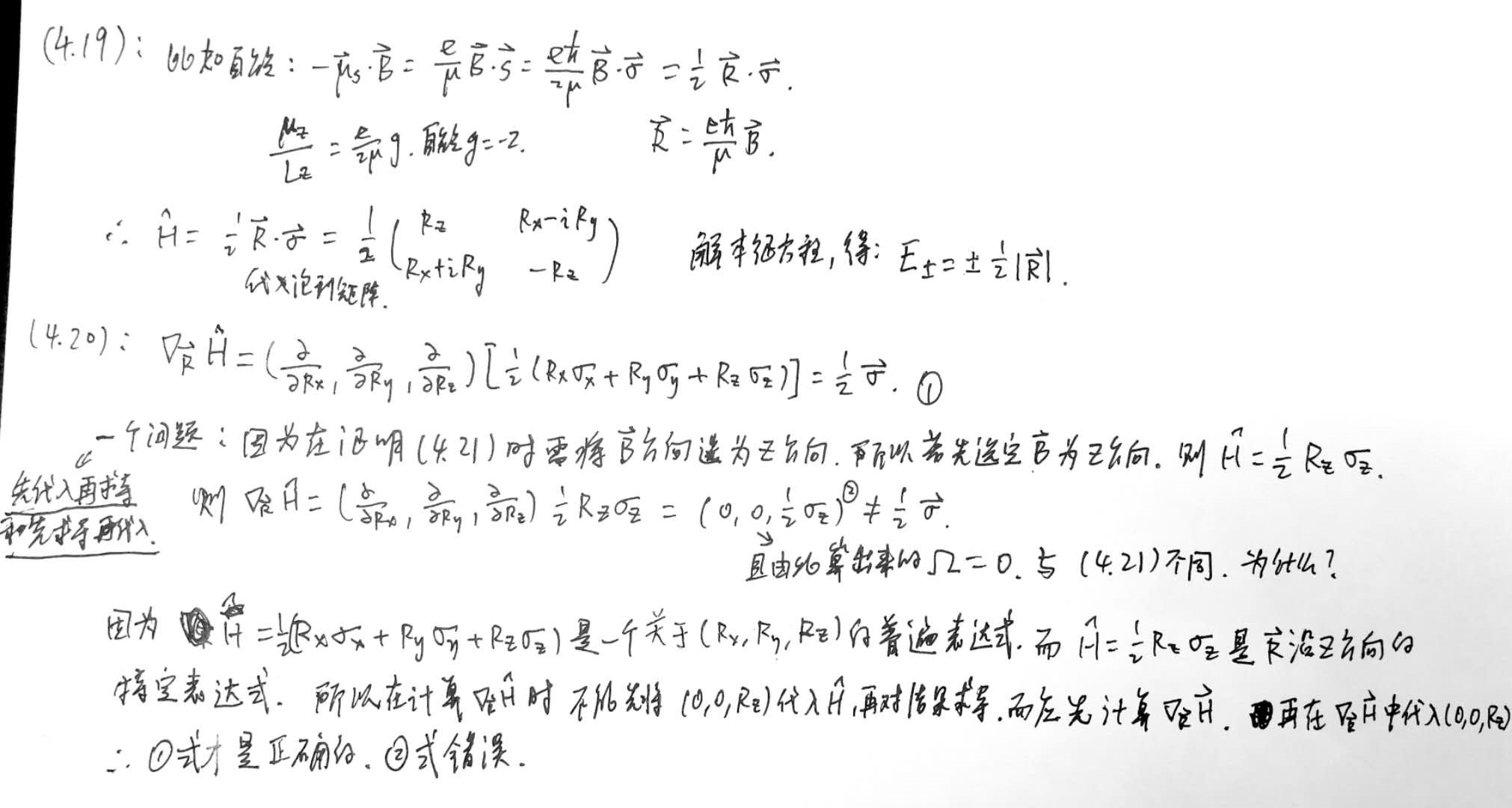
(4.21)、(4.22)证明:

注意:上面的(4.21)式证明中说了选z轴平行于R,其实就是旋转系统的坐标轴使得R位于z轴。上面(4.21)式虽然是R位于z轴的情况下得到的,但旋转不变性意味着(4.21)式在R不位于z轴的一般情况也成立。旋转不变性应该有论文证明了。(这两句话在Bernvig书2.3.2节有)
(4.23)的证明可能需要像电磁学中证明电场的高斯定理一样(所以要证明应查电磁学书),需要对任何闭合曲面都证明(4.22)式,从而由任意闭合曲面都成立的(4.22)式和散度的体积分等于面积分从而证明(4.23)。(4.23)式可能不重要,证明略。
】
在布洛赫能带中,贝里曲率定义为:
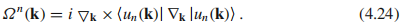
因为布里渊区在动量空间中有周期边界条件,布里渊区中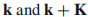 两个点是相同的,其中K是倒格矢,一个闭合路径能被实现当
两个点是相同的,其中K是倒格矢,一个闭合路径能被实现当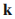 扫过整个布里渊区。在这种情况,穿过布里渊区的贝里相位变成:
扫过整个布里渊区。在这种情况,穿过布里渊区的贝里相位变成:
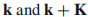 两个点是相同的,其中K是倒格矢,一个闭合路径能被实现当
两个点是相同的,其中K是倒格矢,一个闭合路径能被实现当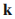 扫过整个布里渊区。在这种情况,穿过布里渊区的贝里相位变成:
扫过整个布里渊区。在这种情况,穿过布里渊区的贝里相位变成: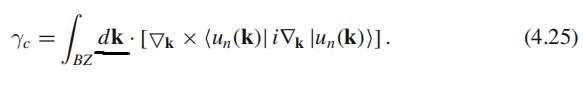
(?)
以下从Bernvig书(2.23)开始的内容接沈顺清的书:

由此式知道,类似点电荷电场公式,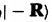 对应的磁单极子强度1/2.而对
对应的磁单极子强度1/2.而对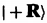 能带,磁单极子有相反的强度-1/2.因此,我们发现参数空间的简并点具有源和漏的作用。如果我们在包含磁单极子的球面上对贝里曲率积分,我们得到2pi,因此贝里曲率在一个闭合流形上的积分等于2pi乘以里面包含的单极子的净数量。(如果我们有另一个简并度点,它会是2。)【?不懂闭合流形】
能带,磁单极子有相反的强度-1/2.因此,我们发现参数空间的简并点具有源和漏的作用。如果我们在包含磁单极子的球面上对贝里曲率积分,我们得到2pi,因此贝里曲率在一个闭合流形上的积分等于2pi乘以里面包含的单极子的净数量。(如果我们有另一个简并度点,它会是2。)【?不懂闭合流形】
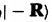 对应的磁单极子强度1/2.而对
对应的磁单极子强度1/2.而对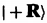 能带,磁单极子有相反的强度-1/2.因此,我们发现参数空间的简并点具有源和漏的作用。如果我们在包含磁单极子的球面上对贝里曲率积分,我们得到2pi,因此贝里曲率在一个闭合流形上的积分等于2pi乘以里面包含的单极子的净数量。(如果我们有另一个简并度点,它会是2。)【?不懂闭合流形】
能带,磁单极子有相反的强度-1/2.因此,我们发现参数空间的简并点具有源和漏的作用。如果我们在包含磁单极子的球面上对贝里曲率积分,我们得到2pi,因此贝里曲率在一个闭合流形上的积分等于2pi乘以里面包含的单极子的净数量。(如果我们有另一个简并度点,它会是2。)【?不懂闭合流形】此贝里曲率在二维闭合曲面上的积分是一个整数(以2pi为单位)。这个整数称为Chern数。【?这句话的证明与上一句话有关,还不懂】
2.3.2 使用哈密顿方法求两能级系统
为了去真正理解一些东西,需要能去用不同的方法推导它。现在用一个规范不变的方法。

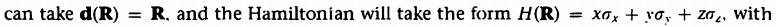
书中直到(2.27)的内容见为知笔记沈书第四章,内容相同。
磁单极子位于简并点R=0(在沈书的情况,R=0对应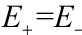 )。
)。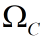 是回路C对应的对简并点的立体角。从(2.27)知:相位因子独立于生成C的封闭曲面的选择(即和封闭曲面的选择无关),因为
是回路C对应的对简并点的立体角。从(2.27)知:相位因子独立于生成C的封闭曲面的选择(即和封闭曲面的选择无关),因为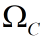 只能通过4pi的倍数发生变化。
只能通过4pi的倍数发生变化。
【(2.27)证明:

】

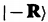 能级,所以我觉得闭合曲线应该对应一个等能线,但这里说不用对应,为什么】。我们刚才是证明了二维无能隙狄拉克费米子的本征态在经过费米面时贝里相位等于pi【根据(2.27)确实】。我们后面还会回到这里。
能级,所以我觉得闭合曲线应该对应一个等能线,但这里说不用对应,为什么】。我们刚才是证明了二维无能隙狄拉克费米子的本征态在经过费米面时贝里相位等于pi【根据(2.27)确实】。我们后面还会回到这里。tuning 选择;subtended 对应
2.4 磁场中的自旋 略
2.5 贝里相位能测量吗
如果一个物理性质不能测量,则它在实验上不是有趣的。贝里相位具有重要的可测量的结果——本书的全部主题在某种程度上都是基于Berry相的结果。 但是,提出一个不涉及任何在晶格上的电子的简单实验非常容易。 想象一下Berry的论文[35]中提出的以下实验。 具有确定自旋态n的一束粒子被分开在两条路径中。 在一条路径上,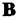 恒定,而在另一条路径上,
恒定,而在另一条路径上,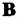 的大小恒定,但其方向围在绕着闭合路径C时缓慢变化,该路径C对应着一个立体角
的大小恒定,但其方向围在绕着闭合路径C时缓慢变化,该路径C对应着一个立体角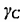 。 通过这样的场的配置后,两个粒子束在探测器处汇合。 由于能量
。 通过这样的场的配置后,两个粒子束在探测器处汇合。 由于能量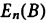 仅取决于B的大小,而B的大小都是相同的,因此两个粒子束的动力学相因子相同。 但是,经历了
仅取决于B的大小,而B的大小都是相同的,因此两个粒子束的动力学相因子相同。 但是,经历了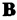 变化的粒子束获得了贝里相位。 衍射图样的强度为
变化的粒子束获得了贝里相位。 衍射图样的强度为
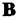 恒定,而在另一条路径上,
恒定,而在另一条路径上,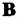 的大小恒定,但其方向围在绕着闭合路径C时缓慢变化,该路径C对应着一个立体角
的大小恒定,但其方向围在绕着闭合路径C时缓慢变化,该路径C对应着一个立体角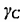 。 通过这样的场的配置后,两个粒子束在探测器处汇合。 由于能量
。 通过这样的场的配置后,两个粒子束在探测器处汇合。 由于能量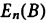 仅取决于B的大小,而B的大小都是相同的,因此两个粒子束的动力学相因子相同。 但是,经历了
仅取决于B的大小,而B的大小都是相同的,因此两个粒子束的动力学相因子相同。 但是,经历了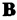 变化的粒子束获得了贝里相位。 衍射图样的强度为
变化的粒子束获得了贝里相位。 衍射图样的强度为
随着磁场缓慢地变化,当经过路径C时,强度变化可以测量出来。
参考资料:
1.沈顺清拓扑绝缘体书
2.汪德新量子力学书
3.bernevig拓扑绝缘体书
4.D. Xiao, M.-C. Chang, and Q. Niu, Berry phase effects on electronic properties, Reviews of Modern Physics 82, 1959 (2010).
5.M.Lax的书: symmetry principles in solid state and molecular physics.
————本文由 初心如磐使命在肩!编辑

