量子自由电子论
一、金属中自由电子的量子态
设金属是边长为 L 的立方体，体积\(V=L^{3}\)，金属中有N个自由电子。
1）由于采用独立电子近似从而忽略了电子电子相互作用，且忽略电子-电子碰撞（为知笔记“第一章翻译”解释了电子-电子碰撞是不重要的），所以N个电子的问题转化为单电子问题。
2）要使自由电子逸出金属外， 必须克服电子的逸出功， 因此金属中自由电子的能态， 可以从在一定深度的势阱中运动的粒子能态估算， 通常设势阱深度是无限的（因为计算更方便），所以这是三维无限深势阱问题。
单电子波函数\(\varphi ( r )\)满足的不含时薛定谔方程为：
\(\left( \frac { \hbar ^ { 2 } } { 2 m } \nabla ^ { 2 } + V ( r ) \right) \varphi ( r ) = E \varphi ( r )\)（矢量符号应该写）
E：电子的本征能量
\(V ( r )\)：平均势场：将电子和离子之间的相互作用用一个为常数的平均势场来表示，还可见“第一章翻译”。 通常取平均势场\(V ( r )\)=0.（这里没有说采用独立电子近似忽略电子-离子相互作用，“第一章翻译”中解释了电子-离子相互作用不是绝对忽略，其实说独立电子近似忽略了电子离子相互作用实际上的含义为将电子和离子之间的相互作用用一个为常数的平均势场来表示，通常取平均势场=0，所以看上去忽略了电子离子相互作用）
此时，薛定谔方程为：
相应的电子速度：$$\mathbf{v} = \frac { \mathbf{p} } { m } = \frac { \hbar \mathbf{k} } { m }$$
E也可以写成：$$E=\frac{1}{2}mv^{2}$$
单电子本征能量：
（注意电子能量取值只能为本征能量，即能级。在非定态即定态的叠加态，电子能量不确定，当观测时，波函数坍缩到本征态）
二、能态密度
（其实能态密度在固体物理新笔记本有推导，这里再写一下）
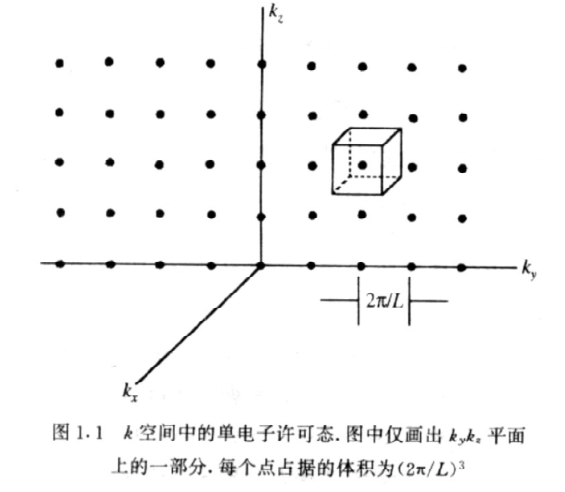
- 求能态密度：
k空间一个态对应的体积为：
由于\(E _ { k } = \frac { \hbar ^ { 2 } k ^ { 2 } } { 2 m } = \frac { \hbar ^ { 2 } } { 2 m } \left( k _ { x } ^ { 2 } + k _ { y } ^ { 2 } + k _ { z } ^ { 2 } \right)\)，所以等能面是球面。
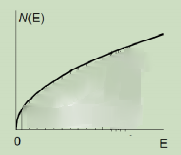
因为能态密度\(N\left ( E \right )=\frac{{dZ}'}{dE}\)、\({dZ}'=\frac{{d\omega }'}{h^{r}}\)
- 求 dE能量间隔对应的k空间体积：
在k空间中E 和 E + dE的等能面分别对应于k和k+dk（注意已经考虑了简并度，一个球面的点就是这个能量E对应的量子态即考虑了简并度）。所以dE能量间隔对应的k空间体积为\({d\omega }'=4\pi k^{2}dk\) \(4 \pi k ^ { 2 }\)是面积
所以\({dZ}'=2\times\frac{4\pi k^{2}dk}{\left ( \frac{2\pi }{L} \right )^{3}}\) (考虑自旋，所以乘2，注意新笔记本上没有考虑自旋，所以新笔记本上算出来的能态密度最后还要乘2才是真正的能态密度） - 由能态密度\(N\left ( E \right )=\frac{{dZ}'}{dE}\)和\(E=\frac{ħ^{2}k^{2}}{2m}\)，得能态密度：
其中常数：
- 电子能级越高,则能态密度越大,由于\(dZ=N(E)dE\),所以\(dE\)间隔中的量子态数越大,由于dZ也是简并度(见热统笔记本),故能级越高,能级上的量子态数越多(等能面的量子态数越多,但此能态密度还考虑了自旋).并不是能级越密,能级的密度由\(E \left( n _ { x } , n _ { y } , n _ { z } \right) = \frac { ħ ^ { 2 } } { 2 m } \left[ \left( \frac { 2 \pi } { L } n _ { x } \right) ^ { 2 } + \left( \frac { 2 \pi } { L } n _ { y } \right) ^ { 2 } + \left( \frac { 2 \pi } { L } n _ { z } \right) ^ { 2 } \right]\)决定.
三、T=0时（即基态）电子气体的性质
见热力学统计物理笔记本“零温时电子气体的性质”
-
费米能的推导的记忆：热力学统计物理笔记本
另一种推导：
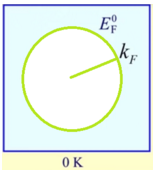
- 求能量小于费米能的量子态数（考虑自旋）：\(2\times \frac{\frac{4}{3}\pi k_{F}^{3}}{\left ( \frac{2\pi }{L} \right )^{3}}\)
- 由于是费米子，有一个个体量子态只能有一个费米子，所以此式也等于总电子数：\(2\times \frac{\frac{4}{3}\pi k_{F}^{3}}{\left ( \frac{2\pi }{L} \right )^{3}}=N\)
由此求出费米波矢、费米能
-
费米能级：T=0K时占据的最高能量
其中费米波矢：\(k_{F}=\left (3\pi^{2}n\right )^{\frac{1}{3}}\)
电子浓度：\(n=\frac{N}{V}\)
- 费米动量\(p _ { F } = \hbar k _ { F }\)
费米速度\(v _ { F } = \frac { \hbar k _ { F } } { m }\)
费米温度\(T _ { F } = \frac { \varepsilon _ { F } } { k _ { B } }\)
费米温度大概几万k，有的金属十几万k
费米能大概几个电子伏特，有的金属十几个电子伏特 - 零温时的费米面的能态密度：
（将费米能表达式代入能态密度表达式得到）记
- 平均动能：T=0K时每个电子的平均能量：
T=0K时系统内能：\(U\left ( 0 \right )=\frac{3}{5}NE_{F}^{0}\)
（由于是费米子，一个个体量子态只有一个费米子，所以\(N\left ( E \right )dE\)是电子数。）
在零温时，电子仍具有较高的平均动能，且计算表明，在零温时电子仍有很高的平均速度\(v - 10 ^ { 6 } \mathrm { m } / \mathrm { s }\)。这与经典理论不同，能量均分定理得到的电子平均动能\(\frac{3}{2}k_{B}T\)，在零温时应为0.
四、T>0时电子气体的性质
- 费米分布函数：
- 统计物理中：\(f _ { j} = \frac { 1 } { e ^ { \left( \varepsilon _ { j } - \mu \right) / k _ { B } T } + 1 }\)
j：粒子量子态序号 \(\mu\)：化学势
对费米狄拉克分布来说，\(f\)是能级\(l\)里简并的各个态上有粒子的平均概率（见热统笔记本“玻尔兹曼分布”一节）。 - 固体物理中写成：\(f ( E ) = \frac { 1 } { e ^ { \frac { E - E _ { F } } { k _ { B } T } } + 1 }\)
\(f\)是能级\(E\)里简并的各个态上有粒子的平均概率
（\(E\)实际上是统计物理表达式中的 \(\varepsilon _ { j }\)，即 \(E _ { j }\)，j：粒子量子态序号）
- 费米能：
- T>0时费米能\(E_{F}\)的定义：即费米分布函数中的化学势 \(\mu\).
T>0时在电子的费米能级\(E_{F}\)里简并的各个态上有粒子的平均概率为\(f(E_{F})=\frac { 1 } { e ^ { \frac { E_ { F } - E _ { F } } { k _ { B } T } } + 1 }=\frac{1}{2}\)，即电子占据概率为\(\frac{1}{2}\) - 由\(N = \int _ { 0 } ^ { \infty } f ( E ) N ( E ) dE\) 和sommerfeld展开式得到T>0时费米能：(注1)
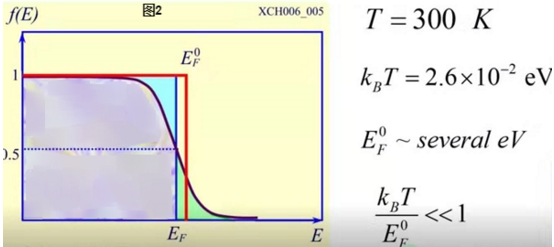
（此图夸张地画出了\(E_{F}\)和\(E_{F}^{0}\)的差别，实际上相差几万分之一，差别很小）
在300k时，\(\frac{k_{B}T}{ E_{F}^{0}}\)大概是几百分之一，平方之后是几万分之一，所以在温度不是很高时（如室温），费米能相对零温时只有很小的下降，近似认为\(
E _ { F } \approx E _ { F } ^ { 0 }\).(如图三中500k时的f的图像)
2)
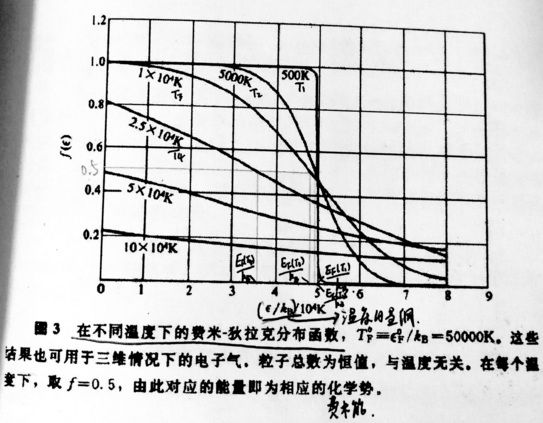
在温度在几百k的基础上以10的倍数增加时，由T>0时费米能表达式和类似300k时的分析可知费米能相对零温时下降很大。（注意是相对零温费米能下降很大，费米能下降数值为\(\frac { \pi ^ { 2 } } { 12 } \left( \frac { k _ { B } T } { E _ { F } ^ { 0 } } \right) ^ { 2 } E_{F}^{0}\)，该数值计算可知很小（因为\(k _ { B }\)为\(1.38\times 10^{-23}\)），但是相对零温的下降\(\frac { \pi ^ { 2 } } { 12 } \left( \frac { k _ { B } T } { E _ { F } ^ { 0 } } \right) ^ { 2 }\)计算可知很大）（但其实\(10^{4}K\)这样的高温远高于金属熔点，金属熔点一般几百或几千K，熔点最高的金属钨为三千多K，这里只是为了讨论而假设. 当金属熔化体积改变可能就不能用自由电子气体模型.)
3)在室温时
- 系统内能：
由\(U = \int _ { 0 } ^ { \infty } E f ( E ) N ( E ) d E\)和sommerfeld展开式得到T>0时系统内能：
第一项为零温时系统内能\(U\left ( 0 \right )=\frac{3}{5}NE_{F}^{0}\)
第二项为总的热激发能（因为温度升高才产生的能量）
对热激发能的理解：
- 只有T时的费米能\(E_{F}\)以下\(k_{B}T\)范围的电子才能被激发的原因：
1）定量: 图三，对大于0的任何温度T,
当\(E\)比T时的\(E_{F}\)大几个\(k_{B}T\)时,\(f ( E ) = \frac { 1 } { e ^ { \frac { E - E _ { F } } { k _ { B } T } } + 1 }\approx0\)
当\(E\)比T时的\(E_{F}\)小几个\(k_{B}T\)时,\(f ( E ) = \frac { 1 } { e ^ { \frac { E - E _ { F } } { k _ { B } T } } + 1 }\approx1\)
(如\(E\)比T时的\(E_{F}\)小1个\(k_{B}T\)时,\(f ( E- k_{B}T) = \frac { 1 } { e ^ { -1 } + 1 }\approx0.731\)
\(E\)比T时的\(E_{F}\)小2个\(k_{B}T\)时,,\(f ( E-2k_{B}T ) = \frac { 1 } { e ^ { -1 } + 1 }\approx0.881\)
\(E\)比T时的\(E_{F}\)小3个\(k_{B}T\)时,,\(f ( E-3k_{B}T ) = \frac { 1 } { e ^ { -1 } + 1 }\approx0.953\),很接近1)
故f的图像与阶梯函数的图像的差别近似仅仅发生在这6个\(k_{B}T\)范围,当T在室温附近时,根据图2下面的分析知:\(k_{B}T\approx0.01E_{F}^{0}\approx0.01E_{F室温}\) (注2)
则:\(6k_{B}T\approx0.06E_{F室温}\)
所以这6个\(k_{B}T\)范围在f的图像中相对于费米能\(E_{F室温}\)很小(f的图像见图三中500k时的情形).
由于f是电子占据概率,所以图三500k时f的图像显示比\(E_{F 500k}\)低\(3k_{B}T\)范围中电子占据概率下降,而比\(E_{F 500k}\)高\(3k_{B}T\)范围中电子占据概率上升.在有很多电子时,也是电子数目的下降和电子数目的上升.
在能级\(E=E_{F 500k}-3k_{B}T\),电子占据概率为0.953,比1下降很小,即很少数目的电子被激发,在能级\(E=E_{F 500k}-2k_{B}T\)也同理.但在能级\(E=E_{F 500k}-k_{B}T\),电子占据概率为0.731,比1下降很多.故在\(E_{F 500k}-k_{B}T至E_{F 500k}\)范围被激发的电子数目多.故近似认为T时的费米能\(E_{F}\)以下\(k_{B}T\)范围的电子才能被激发.
2）定性:由于泡利不相容原理的限制,离零温费米面较远的电子无法被热激发到更高能级对应的量子态,只有零温费米面附近的电子才能在温度升高时被热激发. - 第二项总的热激发能也能写成\(\frac { \pi ^ { 2 } } { 6 } N \left( E _ { F } ^ { 0 } \right) \left( k _ { B } T \right) ^ { 2 }\).
1） 由1.知只有\(k_{B}T\)范围的电子能被热激发,又因为\(N \left( E _ { F } ^ { 0 } \right)\)是单位能级间隔内的总的量子态数,\(k_{B}T\)是能量范围,故热激发电子的数目是\(N \left( E _ { F } ^ { 0 } \right) \left( k _ { B } T \right)\).
2）由于\(E_{F}\)以下\(k_{B}T\)范围的电子热激发到\(E_{F}\)以上\(k_{B}T\)的范围,故被热激发的每个电子获得的能量的量级大概为\(k_{B}T\)(注3)
3）综上,\(\left[ N \left( E _ { F } ^ { 0 } \right) \left( k _ { B } T \right) \right] \left( k _ { B } T \right) = N \left( E _ { F } ^ { 0 } \right) \left( k _ { B } T \right) ^ { 2 }\)即为定性估算的总的热激发能的量级,与定量计算的总的热激发能只相差\(\pi^{2}/6\)的因子.
- 电子热容
分别对系统内能两个等价表达式（1）（2）求偏导，得电子热容：
其中\(\gamma\)称为电子比热系数，比例于零温时的费米面的能态密度.
- \(\gamma\)比例于零温时的费米面的能态密度这一结果不仅只适用于自由电子气体模型，在能带理论考虑离子实对电子的作用、电子许可能级形成能带时也正确.所以测量电子比热可以得到零温时费米面的能态密度，这是实验研究费米面性质的一个重要方法。
- 量子理论计算的电子热容远远小于经典理论值：
经典理论的电子热容：\(\frac{2}{3}Nk_{B}T\)
故
由于\(T_{ F }^{ 0 }\)是几万k，所以在一般温度，量子理论计算的电子热容远远小于经典理论值，在室温时是经典理论值的百分之一量级，由此解释了Drude模型中电子热容量的困难.
- 晶格热容和电子热容的比较：
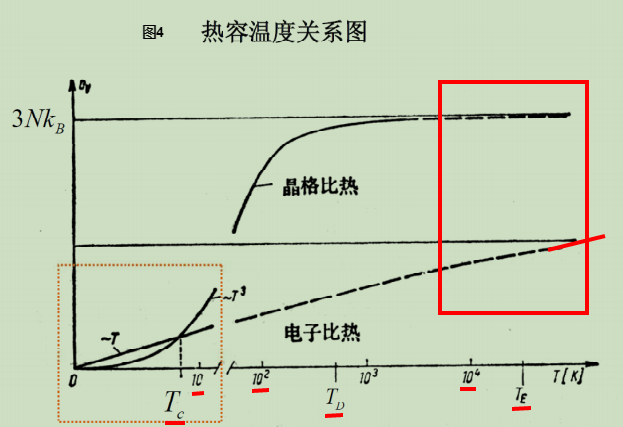
- 摩尔电子热容：1摩尔电子的热容，由将（3）、（4）的热容除以N再乘以阿伏伽德罗常数\(N_{A}\)得到.
- 画出晶格摩尔热容（表达式见北大书134页（5.2.40）或（5.2.34）式，低温表达式见132页（5.2.37）式：\(C _ { V } ^{晶格}=\frac { 12 } { 5 } \pi ^ { 4 } N _ { A } k _ { B } \left( \frac { T } { T _ { D } } \right) ^ { 3 }\)）与电子摩尔热容（表达式\(C _ { V } ^{电子}=\frac { \pi ^ { 2 } } { 2 } N _ { A } k _ { B } \left( \frac { T } { T _ { F } } \right)\)）的函数图像.
- 由低温时
求出交点：
德拜温度\(T _ { D }\)一般是\(10^{2}k\)量级，与实际温度较为接近.零温费米温度\(T _ { F } ^ { 0 }\)一般是几万k.
由\(T _ { D }\sim 10 ^ { 2 }K\),\(T _ { F } ^ { 0 }\sim 10 ^ {4}K\)估算出 \(T _ { C }\sim 1K\)的数量级.
北大书说\(T _ { C }\)大概是在10K左右或更低的温度.
4. 1）\(10^{4}K\)这样的高温远高于金属熔点，所以不考虑.
2）在室温附近或室温以上，由图4（或北大书133页实验和理论得到的晶格比热的图）知，可近似认为晶格热容差不多就是经典值\(\frac{2}{3}Nk_{B}T\)，所以电子热容和晶格热容之比等于上面量子理论计算的电子热容和经典理论值之比。在室温时，电子热容是晶格热容的百分之一量级。（在\(10^{3}K\)可能是十分之一量级）
3）在低温时，晶格热容按\(T_{3}\)下降，最终在10K左右或更低的温度（即\(T _ { C }\)）以下，晶格热容会小于电子热容。在低温时金属总热容：
- 电子比热系数\(\gamma\) 实验值与理论值的差异：
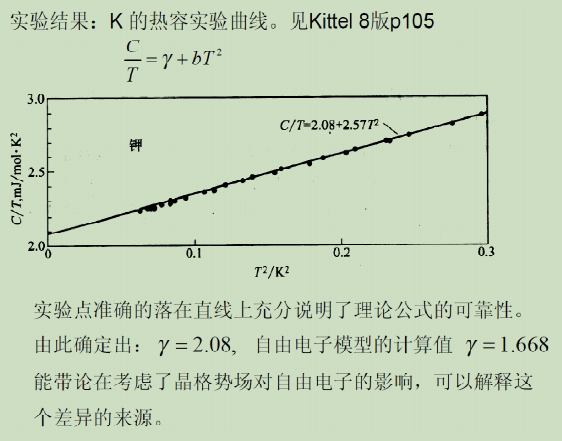
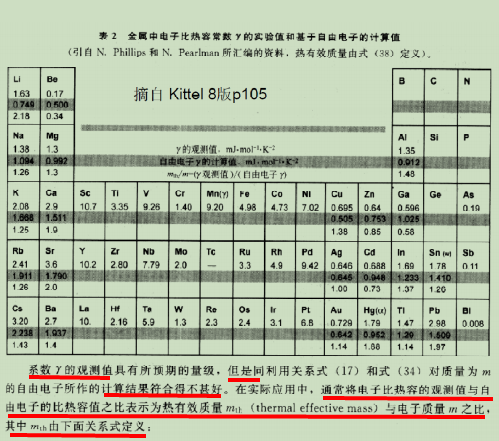
- 电子的顺磁磁化率：课件，北大书13-14页
注1: 费米能、系统内能的推导见课件4.2节补充中“sommerfeld展开式的应用”.
注2: 根据图2下面的分析,其实是\(0.0几E_{F}^{0}\),但是近似写成\(0.01E_{F}^{0}\)
注3: \(k_{B}T\)是猜的?不知道.查solid state书,但没时间.
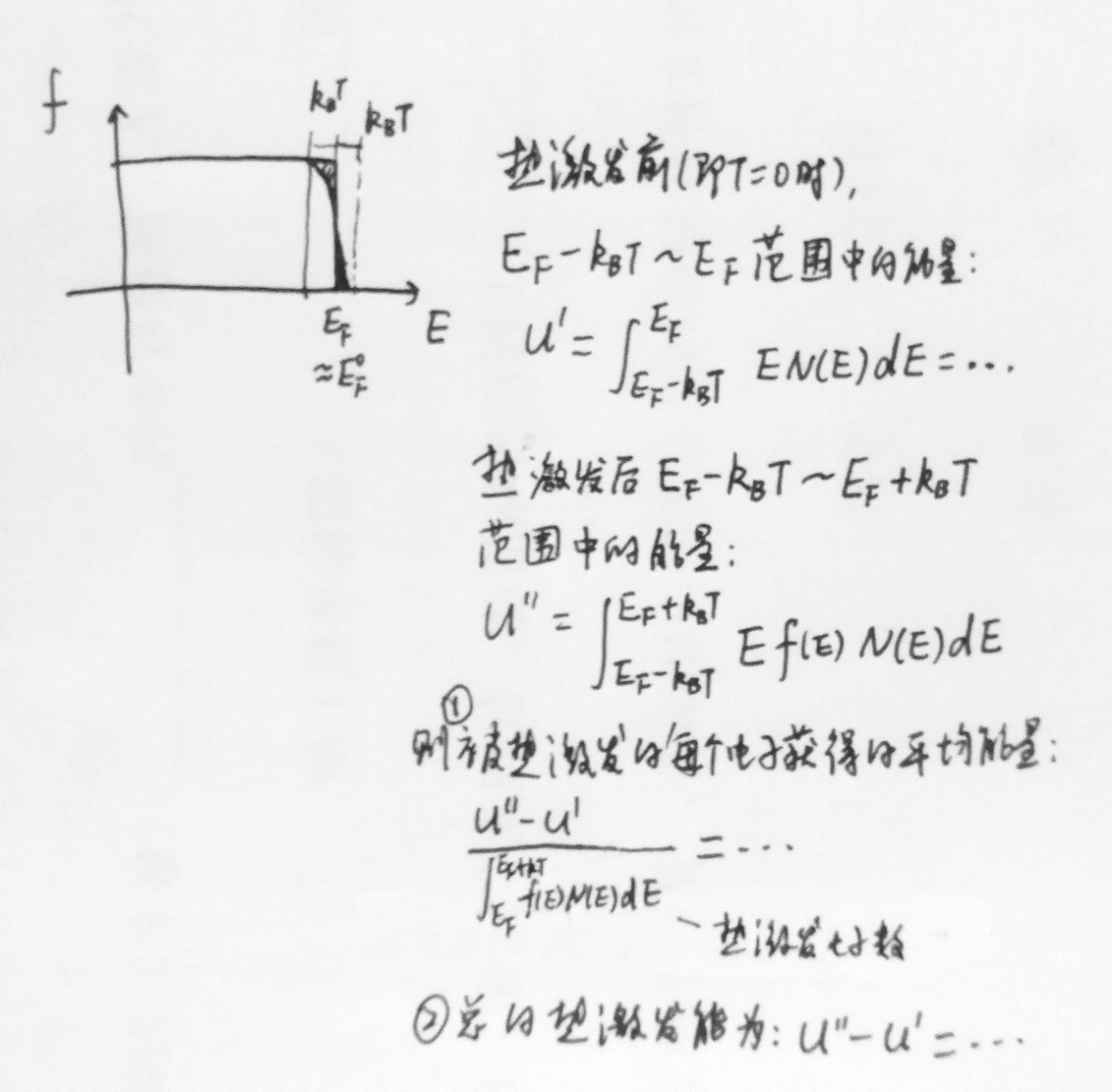
另一种估算总的热激发能(或定量计算被热激发的每个电子获得的平均能量)的方法:
---本文由量子凝聚态编写 （转载需注明来源）
