【算法训练】LeetCode#84 柱状图中最大的矩形

一、描述

84. 柱状图中最大的矩形

给定 n 个非负整数，用来表示柱状图中各个柱子的高度。每个柱子彼此相邻，且宽度为 1 。

求在该柱状图中，能够勾勒出来的矩形的最大面积。

示例 1:

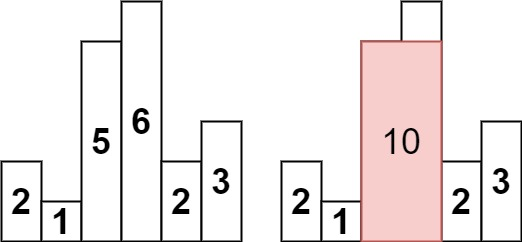
输入：heights = [2,1,5,6,2,3]
输出：10
解释：最大的矩形为图中红色区域，面积为 10

示例 2：

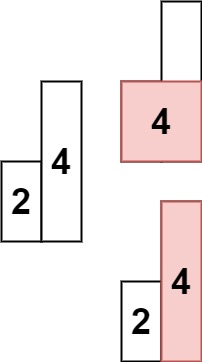
输入： heights = [2,4]
输出： 4

二、思路

1. 这道题不完全是自己做出来的，看了题解
2. 其实与接雨水类似，对于这道题而言，每个矩形能够组成的最大矩形是 “ 其左右两侧小于其高度的矩形组成的区域 ” ，然后通过计算和比较这些区域的面积就得到了最大面积。
3. 所以问题就转化为如何找到对于每个矩形而言的边界，此时就引入了一个概念——单调栈。

三、解题

public static class Solution {
    public int largestRectangleArea(int[] heights) {
        int n = heights.length;
        int[] leftLoc = new int[n]; // leftLoc[i]为i柱左侧第一个小于其高度的柱子的位置，如果没有则-1
        int[] rightLoc = new int[n]; // 同理，右侧
        Deque<Integer> stack = new ArrayDeque<Integer>(); // 单调栈，找到边界的辅助栈，永远存储递增高度的索引
        // 左侧
        for (int i = 0 ; i < n ; i++){
            while (!stack.isEmpty() && heights[stack.peek()] >= heights[i]){
                // 如果不为空且左侧的高度高于本身，则将其认为是能够组成可能最大矩形的柱形，pop
                stack.pop();
            }
            if (stack.isEmpty()){
                // 如果空，则左侧没有比自己低的，存入-1
                leftLoc[i] = -1;
            } else {
                // 如果不为空，则其一定满足 heights[stack.peek()] < heights[i] ,且是左侧第一个满足的loc
                leftLoc[i] = stack.peek();
            }
            stack.push(i);
        }
        stack.clear();
        // 右侧
        for (int i = n-1 ; i >= 0 ; i--){
            while (!stack.isEmpty() && heights[stack.peek()] >= heights[i]){
                // 如果不为空且右侧的高度高于本身，则将其认为是能够组成可能最大矩形的柱形，pop
                stack.pop();
            }
            if (stack.isEmpty()){
                // 如果空，则右侧没有比自己低的，存入 n
                rightLoc[i] = n;
            } else {
                // 如果不为空，则其一定满足 heights[stack.peek()] < heights[i] ,且是右侧第一个满足的loc
                rightLoc[i] = stack.peek();
            }
            stack.push(i);
        }

        // 得到每根柱子的左右边界后，计算且比较即可
        int ans = 0;
        for (int i = 0 ; i < n ; i++){
            ans = Math.max(ans, (rightLoc[i]-leftLoc[i]-1) * heights[i]);
        }
        return ans;
    }
}