【学习】java 二叉树（一）—— 基础认识

一、前言

这里主要是记录自己所学，所以一些基础概念就不再赘述（如二叉树、度、子树等的定义）。

二、构造与遍历

1. 构造

简单的二叉树主要是由值（value）、左子树（left）、右子树（right）构成，遇到具体问题时再此基础上增加属性。

public static class Node{
    public int value;
    public Node left;
    public Node right;

    public Node(int v){
        value = v;
    }
}

2. 遍历

为方便后续书写，这里先给出一棵二叉树作为例子。

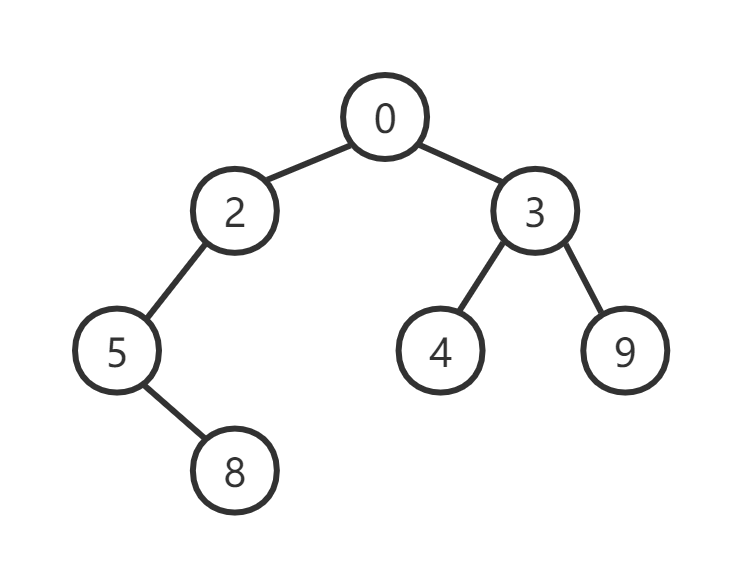
二叉树总体而言有三种遍历方法，分别是：

• 先序遍历
  • 根、左、右
  • 0、2、5、8、3、4、9
• 中序遍历
  • 左、根、右
  • 5、8、2、0、4、3、9
• 后序遍历
  • 8、5、2、4、9、3、0

用代码实现大体上有两种思路，分别是：递归遍历和非递归遍历

2.1 递归遍历

递归遍历顾名思义就是采用递归思想实现三种遍历方法。这里用中序遍历举例，对于树中的每个节点来说，都是做了同样的一件事——找其左、中、右节点（废话~），那么用递归代码实现就会非常简单。

// 中序遍历
public static void in(Node head){
    if (head == null){
        return;
    }
    in(head.left);
    System.out.print(head.value);
    in(head.right);
}

同理

//先序遍历

public static void pre(Node head){
    if (head == null){
        return;
    }
    System.out.print(head.value);
    pre(head.left);
    pre(head.right);
}

// 后序遍历
public static void pos(Node head){
    if (head == null){
        return;
    }
    pos(head.left);
    pos(head.right);
    System.out.print(head.value);
}

2.2 非递归遍历

相较于递归遍历三行代码就能实现先序中序后序，非递归遍历实现起来需要稍微麻烦一点。

非递归先序遍历

这里借助能够实现后进先出的栈结构，将当前节点的非空子节点依照先右后左的顺序入栈，然后pop节点，每次pop时做相同操作即可。由于栈顶元素一定是最新加入栈的节点，入栈顺序又是先右后左，故每次打印根节点后，都会优先遍历左节点，从而实现了先序遍历。

// 先序遍历
public static void pre(Node head){
    System.out.println("先序遍历：");
    if (head != null){
        Stack<Node> stack = new Stack<Node>();
        stack.push(head); // 根节点入栈
        while (!stack.isEmpty()){
            head = stack.pop(); // 出栈
            System.out.print(head.value+" ");
            if (head.right != null){
                // 存在右节点，则入栈
                stack.push(head.right);
            }
            if (head.left != null){
                // 存在左节点，则入栈
                stack.push(head.left);
            }
        }
    }
    System.out.println();
}

非递归后序遍历

非递归的后序遍历与先序相似，将入栈顺序从根、右、左改为根、左、右，并将出栈节点逆序打印即可。这是因为入栈顺序为根、左、右时，出栈顺序为根、右、左，那么逆序就会得到左、右、根。

// 后序遍历
public static void pos(Node head){
    System.out.println("后序遍历：");
    if (head != null){
        Stack<Node> stack = new Stack<Node>();
        Stack<Node> overeStack = new Stack<Node>();
        stack.push(head); // 根节点入栈
        while (!stack.isEmpty()){
            head = stack.pop(); // 出栈
            if (head.left != null){
                // 存在左节点，则入栈
                stack.push(head.left);
            }
            if (head.right != null){
                // 存在右节点，则入栈
                stack.push(head.right);
            }
            overeStack.push(head); // 存储出栈节点
        }

        while (!overeStack.isEmpty()){
            // 逆序打印
            System.out.print(overeStack.pop().value + " ");
        }
    }
    System.out.println();
}

非递归中序遍历

还是要借助栈，由于中序遍历是左根右，那么依照递归序，先将所有左子树入栈，当左子树为空时，当前节点即可打印并出栈，之后再将右节点作为根节点重复上述步骤。

// 中序遍历
public static void in(Node head){
    if (head != null){
        System.out.println("中序遍历：");
        Stack<Node> stack = new Stack<Node>();
        while (!stack.isEmpty() || head != null){
            if (head != null){
                // 当head 不为空时，直接入栈，并遍历左子树
                stack.push(head);
                head = head.left;
            }else {
                // head为空，stack中存在节点，则出栈并遍历右子树
                head = stack.pop();
                System.out.print(head.value + " ");
                head = head.right;
            }
        }
        System.out.println();
    }
}

实现的方法有很多，只要明白遍历的先后顺序就能轻而易举的实现。