Pytorch系列:（九）正则与常用归一化

L1 & L2

L1正则

L1正则算法如下：

\[||x||_1 = \sum_i^n|x_i| \]

其中\(|x_i|\)表示绝对值。

在Pytorch 中，没有自带L1正则方法，所以需要手动写

reg_loss = 0
for param in model.parameters():
    reg_loss += torch.sum(torch.abs(param))
    
loss = criteon(logits,target) 
loss = loss + 0.01 * reg_loss

optimizer.zero_grad()
loss.backward()
optimizer.step()
  

L2正则

L2正则计算方法如下：

\[||x||_2 = \sqrt{\sum_i^n x_i^2} \]

在pytorch中，优化器中再带L2正则，使用方法如下：直接设定weight_decay 参数即可。

optim = torch.optim.SGD(net.parameters(), lr = 0.0001, momentum = 0.8, weight_decay=1e-2)

模型中常用四种归一化

在前向传播过程中，模型的数据会出现分布偏移，使用归一化可以将偏移进行校正，对中间输出的值进行归一化。好处是可以加速模型收敛，而且不用精心设计权重初始化。

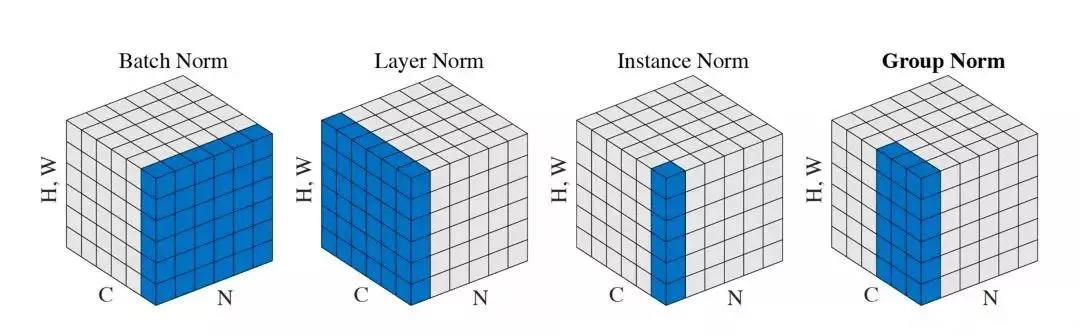
BatchNorm

BatchNorm 计算法方法如下：

\[\begin{align*} \mu_B &= \frac{1}{m}\sum_{i=1}^nx_i \\ \sigma_B^2 &= \frac{1}{m}\sum_{i=1}^m(x_i-\mu_B)^2 \\ \hat x_i &=\frac{x_i-\mu_B}{\sqrt{\sigma_B^2+\epsilon}} \\ y_i &= \gamma \hat x_i + \beta = BN_{\gamma,\beta}(x_i) \end{align*} \]

在pytorch中，Batch Normalization 模块一般放置在激活函数前面。其函数如下：

nn.BatchNorm1d()
nn.BatchNorm2d()
nn.BatchNorm3d()

参数：

num_feature: 样本的特征数量

eps: 分母修正项

momentum: 指数加权平均，用于计算均值方差

affine: 是否要进行affine transform ，意思是是否计算 \(y_i = \gamma \hat x_i + \beta\)

track_running_stats: 表示是否估计新的均值和方差，如果是训练阶段，会计算每一个batch的的均值和方差，如果是测试阶段，均值和方差是固定的。

Batch中的主要属性：

running_mean：均值

running_var：方差

weight: affine transform 中的 gamma, 既\(\gamma\)

bias : affine transform中的beta, 既\(\beta\)

需要注意的是，如果设置了momentum，那么均值的计算会考虑上次的均值

\[\begin{align*} running\_mean &= (1-momentum)*pre\_running\_mean + momentum* \mu_B \\ running\_var &=(1-momentum)*pre\_running\_var+momentum*\sigma_B^2 \end{align*} \]

BatchNorm 的核心是，对于每一个batch的数据，假设有N个特征，这个N个特征中，对应位置的特征，会被BatchNorm放到一起计算，对于1D，2D，和3D ，唯一的区别就是计算的时候，特征的维度。具体来说：

# 这里每一个特征维度是1维，尺寸为N 
input(BatchNorm1D) : ( batch , num_features, 1*N）

# 这里每一个特征的维度是2维度，常用于图像，对应featrue map的长和宽
input(BatchNorm2D) : ( batch , num_features, width, height) 
# 这里每一个特征的维度是3维度，常用语3位数据，可以理解为多个图像，
# 既num_of_wh个图像
input: (batch, num_features, width, height, num_of_wh) 

Layer Normalization

Layer Normalization 主要是针对于1维变长序列数据，例如，在自然语言处理中，每一个batch中，句子的长度不一样，这个时候，Layer Normalization就可以用于这种情况，LayerNorm主要计算的是一个batch中，每一个句子自己去做计算，也就是说，每一个样本中，N个特征自己去计算均值和方差，而不是batch之间去计算。 对应于CNN的话，假设每个batch，有N个feature map，然后LayerNorm就是计算每个Batch里面，这个N个feature_map的均值和方差。

Pytorch中对应得LayerNorm函数如下：

nn.LayerNorm()

参数：

normalized_shape: 每一层的形状，也就是长度

eps: 分母修正项

elementwise_affine: 是否需要affine transform

LayerNorm 计算和BatchNorm计算基本一样，区别是，LayerNorm 不是跨batch进行计算的，因此，也就不再有running_mean 和 runing_var了。

在使用的时候，Layer需要注意的是，设置normalized_shape, 其实就是设置特征的尺寸，这个和BatchNorm不同，BatchNorm主要设置的是特征的个数。另外，这里的LayerNorm也可以处理不同维度特征，只需要设置特征的尺寸就可以了。具体使用方式如下：

# input 1D : (batch, seq_len, N)  主要针对序列数据，每句话长度为seq_len，维度为N，这个时候
# LayerNorm需要将normalized_shape设置成N
layer_norm = nn.LayerNorm((N),eps=0.0001,elementwise_affine=True)


# input2D : (batch, num, width, height) 主要针对图像数据，有num个feature map，
# 尺寸为（width, height）
layer_norm  = nn.LayerNorm((width,height),eps=0.0001,elementwise_affine=True)

# input3D : (batch, num, width, height, num_of_wh)
layer_norm = nn.LayerNorm((width,height,num_of_wh),eps=0.0001,elementwise_affine=True)

Group Normalization

第三个是Group Normalization，这里的batch是2，所以估计的均值方差都很小，所以就可以考虑用特征来求均值方差，这个的gamma和beta还是对应于特征数

Group Normalization和LayerNorm比较相似，只不过，LayerNrom使用所有特征进行计算的，而Group是对特征进行分组计算。

pytorch中对应的函数，这里的num_channels对应的是特征数

nn.GroupNorm()

参数：

num_groups: 分组的个数

num_channels： 通道数，也可以理解为特征的个数

eps ： 分母修正项

affine： 是否需要计算affine transform

需要注意的是，这里也不会计算running_mean 和 running_var.

Instance Normalization

Instance Normalization计算方式如下所示，每一个样本有三个特征，每一个特征自己去计算一个均值方差，所以称为instance Normalization，这个主要用于风格迁移任务中。从卷积网络的角度来理解，就是每一个feature map 自己单独计算均值和方差，这里需要注意的是，输入的参数和BatchNorm一样，也是输入特征数量，每一个特征单独计算的时候，也会加权之前对应位置特征的均值和方差。具体的用法和BatchNorm 一样。

nn.InstanceNorm()

参数：这和上面的BatchNorm参数是一样的

num_features: 样本中有多少特征

eps: 分母修正项

momentum: 指数加权计算均值方差

affine: 是否进行affine transofrm

track_running_stats: 是否重新计算均值方差。