特征工程系列：（四）异常值识别与处理

在进行特征工程的时候，为了确保模型的准确性，需要将一些异常数据排除，从而防止模型被带偏。因此，在特征工程任务中，需要一些方法，来识别异常值。

异常值识别

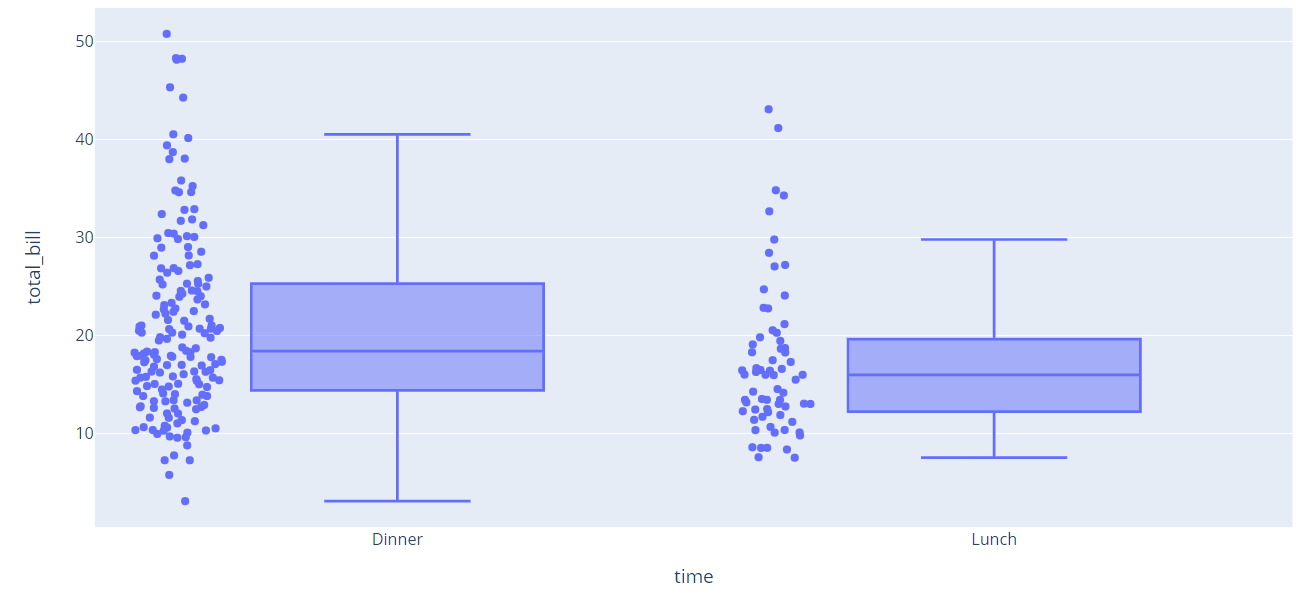
(1) 箱线法

通常用户用某个统计分布对数据点进行建模，再以假定的模型，根据点的分布来确定是否异常。
如通过分析统计数据的散度情况，即数据变异指标，对数据的分布情况有所了解，进而通过数据变异指标来发现数据中的异常点数据。

箱线图是一种用作显示一组数据分散情况资料的统计图，它可以准确的描述数据的离散分布情况。在箱线图中，有一些常用的指标：下分位数Q1，中位数（第二个四分位数），上分位数（Q3），上限和下限，超出上限和下限的值可以被看做是异常值。

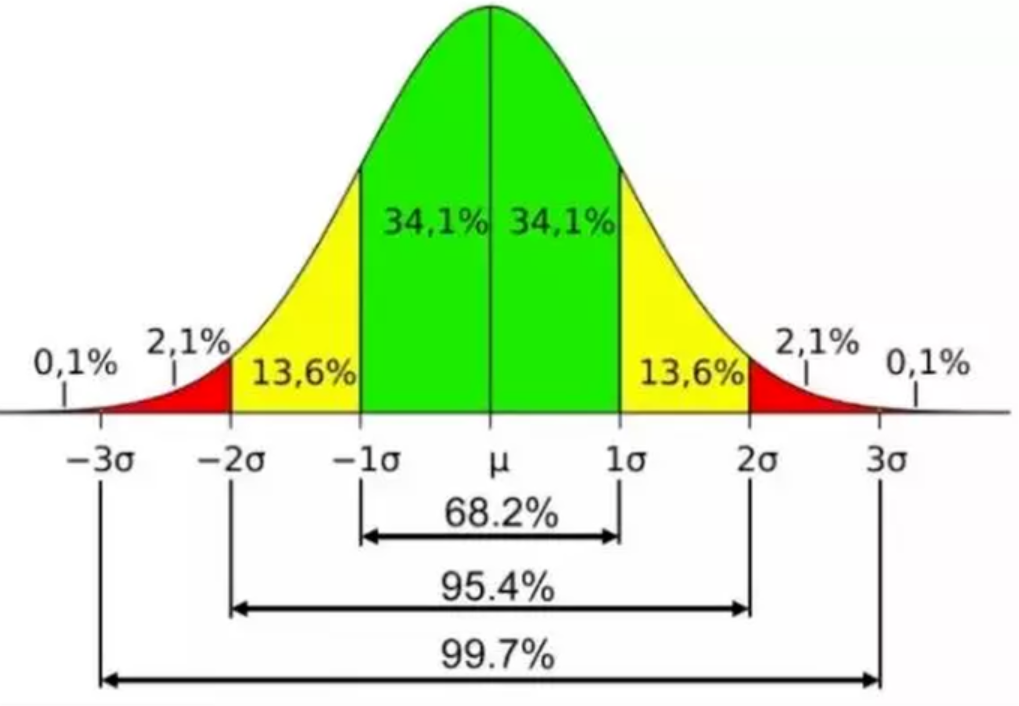
(2) 正太分布图，3σ原则

若数据存在正态分布，在 3σ原则下，异常值为一组测定值中与平均值的偏差超过3倍标准差的值。如果数据服从正态分布，距离平均值3σ之外的值出现的概率为P(|x - μ| > 3σ) <= 0.003，属于极个别的小概率事件。如果数据不服从正态分布，也可以用远离平均值的多少倍标准差来描述。

(3) 基于模型检验

首先建立一个数据模型，如果有些数据，模型无法拟合，那么可以将这些数据看做为异常值。例如使用k-means算法，如果数据距离中心非常远，可以看做是异常值。如果是回归模型，那么如果数据距离回归曲线非常远，那么也可以看做异常值，具体情况要根据实际业务灵活判断。

这个方法的缺点是，对于多元数据，可用的选择少一些，并且对于高维数据，这些检测可能性很差。

(4) 基于距离

基于距离的方法是基于下面这个假设：即若一个数据对象和大多数点距离都很远，那这个对象就是异常。通过定义对象之间的临近性度量，根据距离判断异常对象是否远离其他对象，主要使用的距离度量方法有绝对距离(曼哈顿距离)、欧氏距离和马氏距离等方法。

这个方法的有点是使用起来比较简单，缺点是，对于大数据，计算量会比较大。

(5) 基于密度

考察当前点周围密度，可以发现局部异常点，离群点的局部密度显著低于大部分近邻点，适用于非均匀的数据集。

这个方法的优点是，给出了对象是离群点的定量度量，并且即使数据具有不同的区域也能够很好的处理。缺点是计算量也很大，不适用于大数据。

异常值处理方法

对异常值处理，需要具体情况具体分析，异常值处理的方法常用有四种：

(1) 删除含有异常值的记录；某些筛选出来的异常样本是否真的是不需要的异常特征样本，最好找懂业务的再确认一下，防止我们将正常的样本过滤掉了。

(2) 将异常值视为缺失值，交给缺失值处理方法来处理；

(3) 使用均值/中位数/众数来修正；

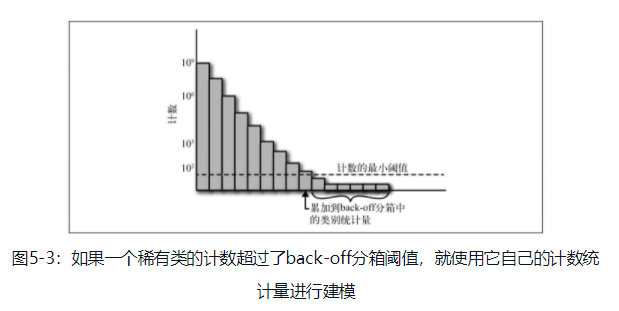
(4) 稀有类back-off
有时候，除了异常值以外，有一些类别中，样本量的个数非常的少，其实也可以将其视作异常值，有一个方法就是，可以将这些稀有类的值，全部放到一个箱子里面，看做为单独的一类。