Codeforces Round 864 (Div. 2)
Codeforces Round 864 (Div. 2)
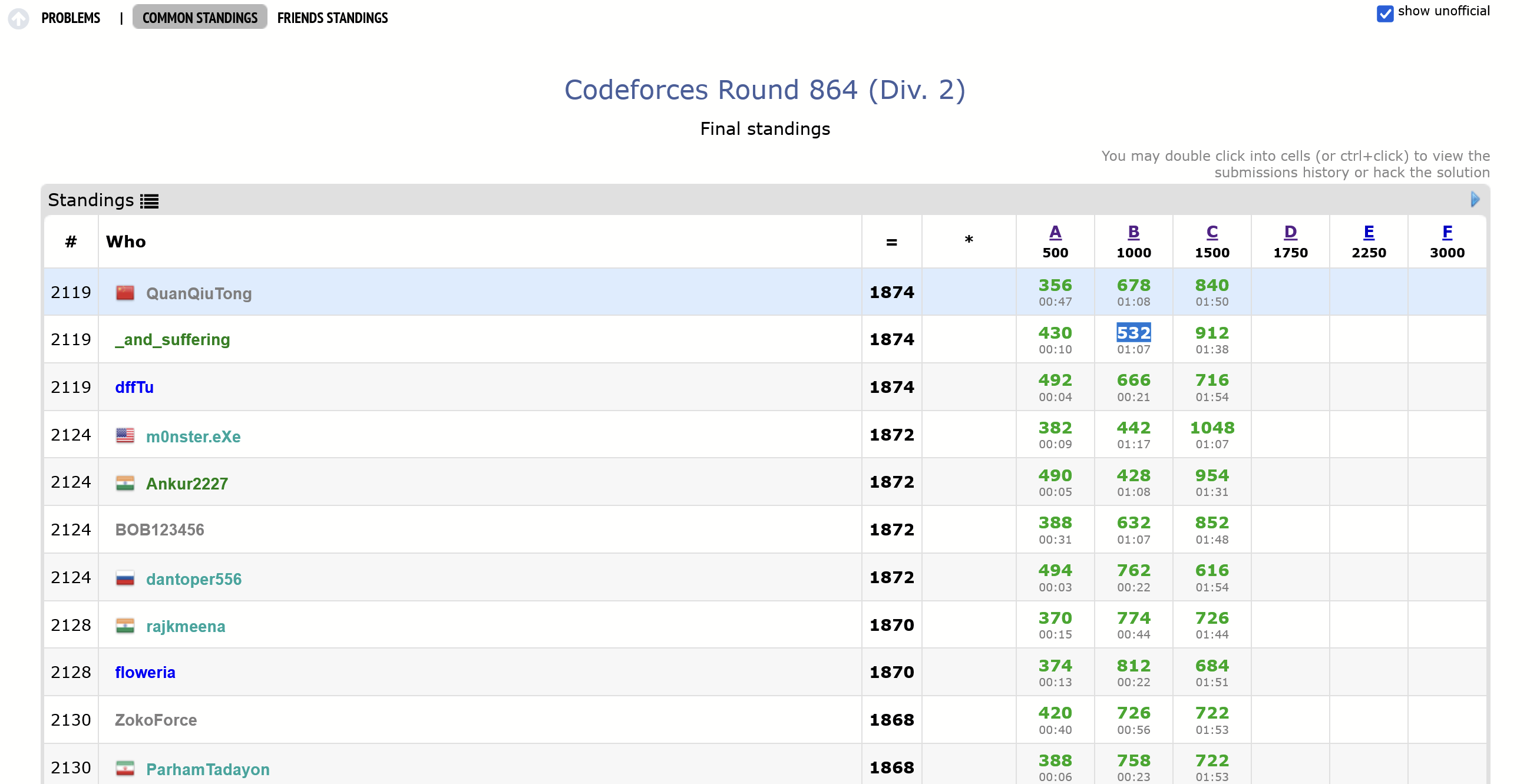
喜提Rating = 883
赛前就留了3个cpp,结果就做出来3个。
不得不说lihua确实呃呃。
A
题面的描述方法以及给出的样例好有迷惑性啊,
其实答案根本不会超过4,把某一个格子周边全部围起来就行了。也就是下面最后2个花括号里面的内容。
int main()
{
for (int t = read(); t--;)
{
int n = read(), m = read(), x1 = read(), y1 = read(), x2 = read(), y2 = read(), ans = 1.1e9;
if (x1 == x2)
{
if (y1 > y2)
swap(y1, y2);
ans = min(n, min(x1, n - x1 + 1) + min(y1, m - y2 + 1));
ans = min(ans, 1 + 2 * min(y1, m - y2 + 1));
}
else if (y1 == y2)
{
if (x1 > x2)
swap(x1, x2);
ans = min(m, min(y1, m - y1 + 1) + min(x1, n - x2 + 1));
ans = min(ans, 1 + 2 * min(x1, n - x2 + 1));
}
else
{
if (x1 > x2)
swap(x1, x2), swap(y1, y2);
// if (abs(y1 - y2) > 1)
ans = min(ans, n);
// if (abs(x1 - x2) > 1)
ans = min(ans, m);
ans = min(ans, 1 + 2 * min(x1, n - x2 + 1));
if (y2 < y1)
{
ans = min(ans, min(y2 + n - x2 + 1, x1 + m - y1 + 1));
ans = min(ans, 1 + 2 * min(y2, m - y1 + 1));
}
else if (y2 > y1)
{
ans = min(ans, min(x1 + y1, n - x2 + 1 + m - y2 + 1));
ans = min(ans, 1 + 2 * min(y1, m - y2 + 1));
}
}
// if(abs(x1-x2)>1){
// ans=min(ans,1+2*min(min(y1,m-y1+1),min(y2,m-y2+1)));
// }
// if(abs(y1-y2)>1){
// ans=min(ans,1+2*min(min(y1,m-y1+1),min(y2,m-y2+1)));
// }
{
int t=4;
if(x1==1||x1==n)t--;
if(y1==1||y1==m)t--;
ans=min(ans,t);
}
{
int t=4;
if(x2==1||x2==n)t--;
if(y2==1||y2==m)t--;
ans=min(ans,t);
}
printf("%d\n", ans);
}
return 0;
}
心急忘了把y1==n改成y1==m,又白白掉了50分,呜呜呜(棒读)。
B
注意n为奇数的时候,正中间那个格子\((\frac{n+1}2,\frac{n+1}2)\)可变可不变,所以只需要k>=cnt就好了。又是-50分呢。
bool g[N][N];
int main()
{
for (int t = read(); t--;)
{
int n = read(), k = read(), cnt = 0;
rep(i, 1, n) rep(j, 1, n) g[i][j] = read();
rep(i, 1, n / 2) rep(j, 1, n) cnt += (g[i][j] != g[n + 1 - i][n + 1 - j]);
if (n & 1)
rep(j, 1, n / 2) cnt += (g[(n + 1) / 2][j] != g[(n + 1) / 2][n + 1 - j]);
// rep(i, 1, n) rep(j, 1, n) cnt += (g[i][j] != g[n + 1 - i][n + 1 - j]);
//printf("%d", cnt);
if(k>=cnt&&(n&1||(k-cnt)%2==0))puts("YES");
else puts("NO");
}
return 0;
}
C
一开始看题面的时候还正确地理解了max<=1是水平条与竖直条的交集,即半径为1的正方形。
结果做起题来的时候又误认为只能上下左右移动(??好好审题之后就把审的题目丢掉了是吧)
然后以为只需要问2次,分别获得主副对角线的序号就能算出坐标了。
改了之后其实思路大差不差,类比欧几里得空间里2个圆相交或相切。
也就是说如果前两个的交点有多个,那么再在“所有交点的连线”的“端点或延长线”上取一点为圆心询问一次。
这正是移动基站定位的做法。
注意到前两个点的取点方式有可能导致(假想的)两个四分之一圆的竖直边出界,使得交边的左端点出界,
故统一改成对横坐标1的询问。不必区分左端点横坐标的正负。
// #pragma GCC optimize(2)
#include <cstdio>
int main()
{
int t, n, m, x, y, z;
for (scanf("%d", &t); t--;)
{
scanf("%d%d", &n, &m);
puts("? 1 1");
fflush(stdout);
scanf("%d", &x);
// if(x==0){
// puts("! 1 1");fflush(stdout);continue;
// }
printf("? 1 %d\n", m);
fflush(stdout);
scanf("%d", &y);
// printf("! %d %d\n", (x + y + 3 - m) / 2, (x - y + 1 + m) / 2);
if (m - y < x + 1)
{
if (x + 1 < y + 1)
printf("! %d %d\n", x + 1, m - y);
else if (x + 1 > y + 1)
printf("! %d %d\n", y + 1, x + 1);
// else if(m-y>=1)
// {
// printf("? %d %d\n", x + 1, m - y);
// fflush(stdout);
// scanf("%d", &z);
// printf("! %d %d\n", x + 1, m - y + z);
// }
else {
printf("? %d 1\n", x + 1);
fflush(stdout);
scanf("%d", &z);
printf("! %d %d\n", x + 1, 1 + z);
}
}
else /* m-y == x+1 */
{
printf("? 1 %d\n", m - y);
fflush(stdout);
scanf("%d", &z);
printf("! %d %d\n", 1 + z, m - y);
}
fflush(stdout);
}
return 0;
}
D
看了一眼 重儿子旋转(rotate)为父节点。感觉应该找到rotate带来的“importance”变化。
后面“复习”树乃至学习有关轻重链剖分的高级知识之后再来做吧。
激动地等待滚榜(Dashboard页面显示我前两题红是怎么回事……是因为我pretest的时候WA了几次么?):
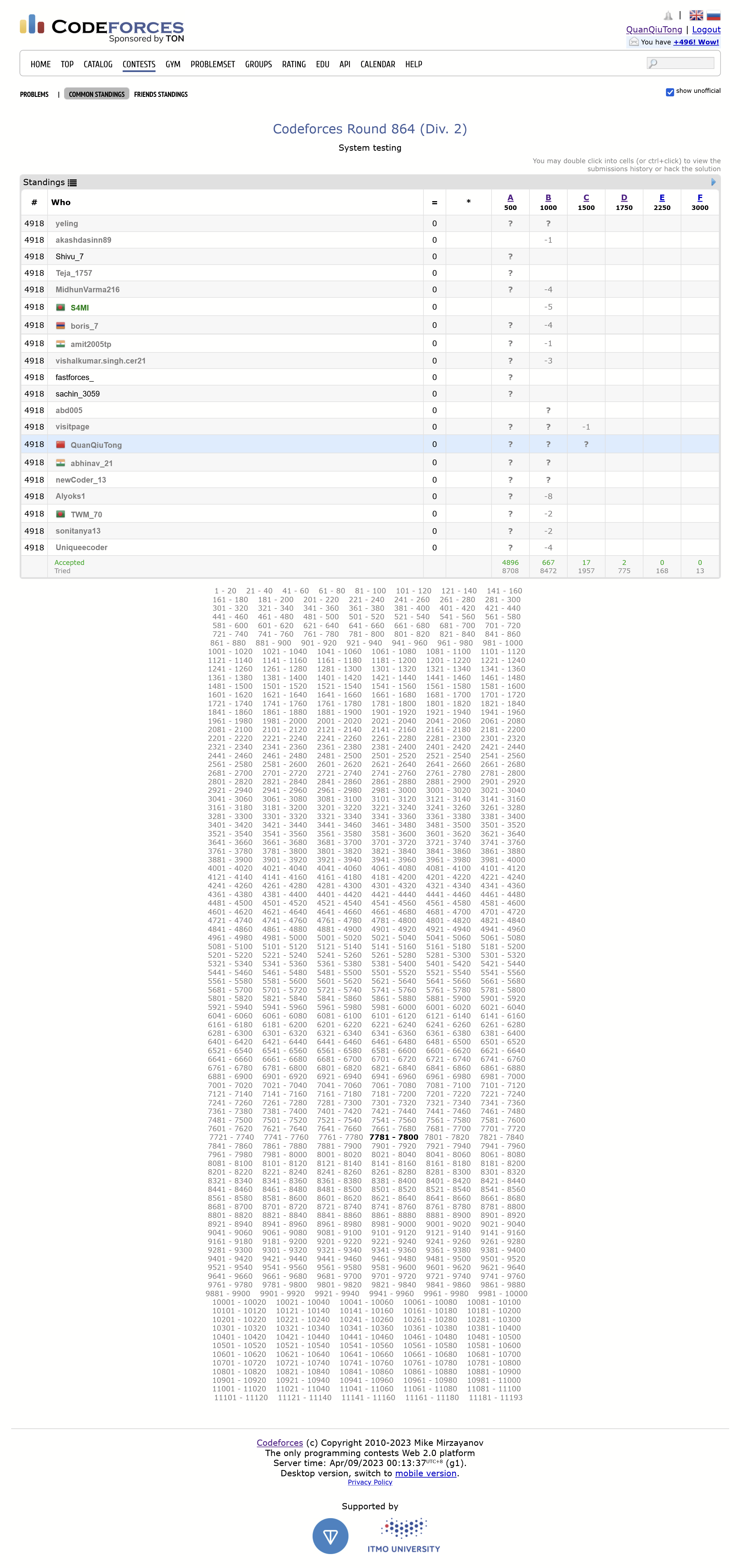
2023年4月9日00:23:55好好好 绿了一个
2023年4月9日00:30:48 很好,又一个
下面是QQ群聊记录
【犭句】 2023/4/8 21:21:24
这次的CF 22:05,早了一点
【犭句】 2023/4/8 22:53:12
mabi 第一题48min
【犭句】 2023/4/8 22:53:17
lihua真是晦气
【犭句】 2023/4/8 22:53:22
【犭句】 2023/4/8 23:13:42
果然恶心 58min才过了这么些人


