周赛_CF758+CF760
第一题感觉就是先求gcd载检查是否正确。不过“检查”这一步骤我不是很会。
constexpr int N=1e2+2;
ll a[N];
#define fail do{puts("0");goto loop;}while(0)
int main(){
for(int t=read();t--;){
int n=read();
for(int i=0;i<n;++i)a[i]=read();
vector<ll> g(a,a+2);
for(int i = 0; i < n; i++)
{
g[i % 2] = __gcd(g[i % 2], a[i]);
}
/*ll odd=a[1],even=a[2];
for(int i=3;i<=n;++i){
if(i&1)
odd=__gcd(odd,a[i]);
else
even=__gcd(even,a[i]);
}
//printf("#odd %lld, even %lld\n",odd,even);
if(odd==even)fail;
else if(even==1){
for(int i=2;i<=n;i+=2)
if(a[i]%odd==0)fail;
}
else if(odd==1){
for(int i=1;i<=n;i+=2)
if(a[i]%even==0)fail;
}
printf("%lld\n",max(odd,even));
loop:;
*/
bool good[2]={1,1};
for(int i=0;i<n;++i)
good[i%2]=good[i%2]&&(a[i]%g[(i%2)^1]>0);
ll ans=0;
if(good[0])ans=max(ans,g[1]);
if(good[1])ans=max(ans,g[0]);
printf("%lld\n",ans);
}
return 0;
}
B
构造题都是“想出来就赢了”。
先构造一上一下的许多交叉项来获取足够数量的max和min,再把剩下的数按顺序放在一端,以确保不会造成新的max或min。
constexpr int N=1e5+2;
#define fail do{puts("-1");goto loop;}while(0)
int p[N];
inline void build(int a,int b,int n){
for(int i=1;i<n-a-b;++i)p[i]=i;
for(int i=1,f=1;i<=a+b+1;++i,f^=1){
p[i+(n-a-b)-1]=f?(n-i/2):(n-a-b-1+i/2);
}
}
int main(){
for(int t=read();t--;){
int n=read(),a=read(),b=read();
if(a+b>n-2||abs(a-b)>1)fail;
if(a>=b){
build(a,b,n);
for(int i=1;i<=n;++i)printf("%d ",p[i]);puts("");
}
else {
build(b,a,n);
for(int i=1;i<=n;++i)printf("%d ",n+1-p[i]);puts("");
}
loop:;
}
return 0;
}
C
最大的k个一定要消去,然后还需要消除次大的k个,并且小的除以小的(按顺序分别除),以减少除出1的数量。
其实就是贪心。两个区间当中谁除以谁并不会影响剩下的元素的加和。
for(int t=read(),a[102];t--;){
int n=read(),k=read(),ans=0;
for(int i=0;i<n;++i)a[i]=read();
sort(a,a+n);
for(int i=0;i<n-2*k;++i)ans+=a[i];
for(int i=0;i<k;++i)ans+=a[n-2*k+i]/a[n-k+i];
printf("%d\n",ans);
}
D
解线性方程组。要求所有的解为正数。
constexpr int N=4e4+2;
#define fail do{puts("NO");goto loop;}while(0)
int a[N],b[N];
int main(){ // 解线性方程组
for(int t=read();t--;){
ll n=read(),sumb=0,d=n*(n+1)/2,suma;
for(int i=0;i<n;++i)sumb+=b[i]=read();
if(sumb%d)fail;
suma=sumb/d;
for(int i = n-1; ~i; i--) {
ll res = (b[i] - b[(i + 1) % n] + suma);
if(res % n != 0 || res <= 0)fail;
a[(i + 1) % n] = res / n;
}
puts("YES");
for(int i=0; i<n; i++)printf("%d ",a[i]);
puts("");
loop:;
}
return 0;
}
E
tarjan缩点后,入度为0的SCC里面的点全是赢家,其余都输。
可以证明,从x开始能跑通全图 等价于 x能跑到max{a}(这个点一定可以跑通全图)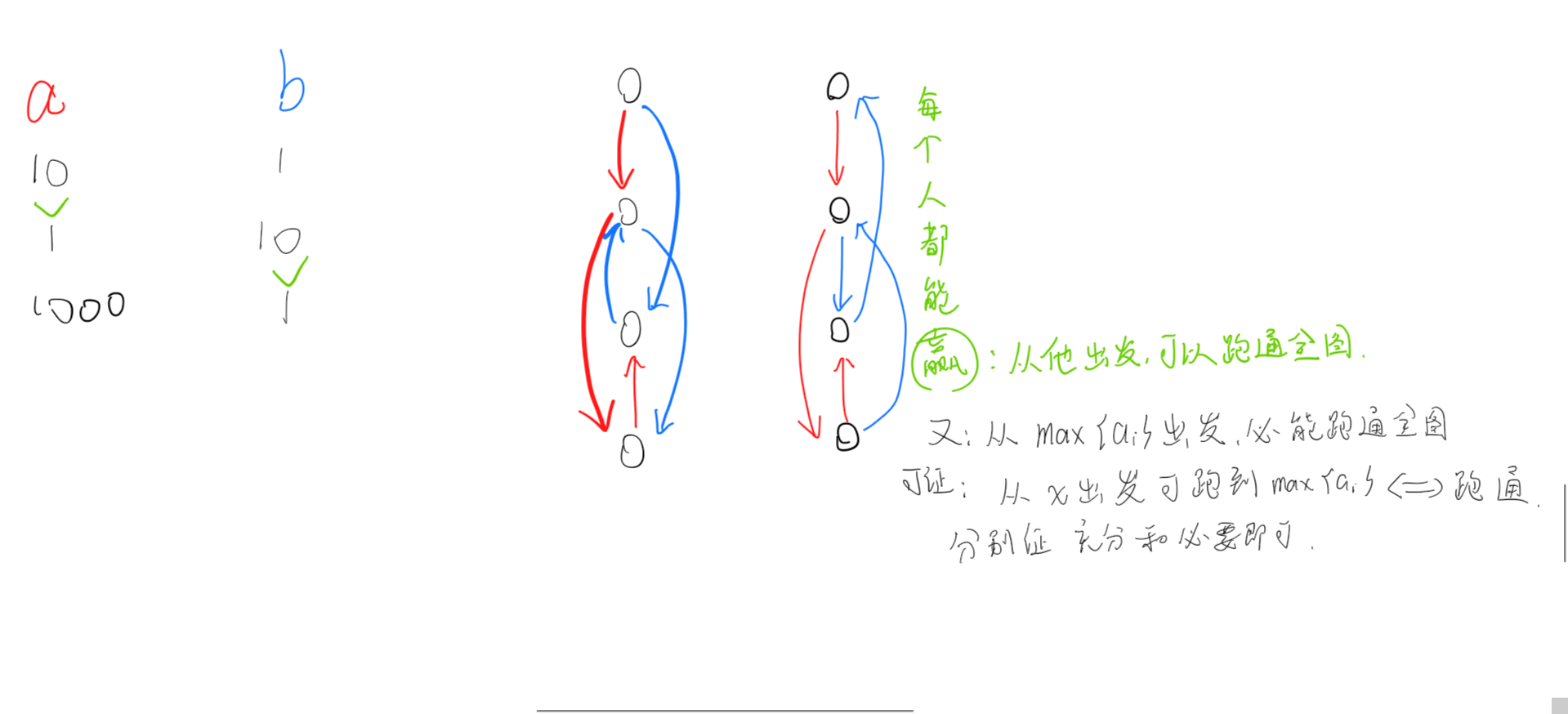
可以找到max,从他开始跑反图,能到达的点即赢家。这等价于在0号SCC里找一个点开始跑反图,反图里面所有到达的点都是赢家。DFS、BFS都行。
由于只有2种边,也可以转成双指针,0个以上返祖边覆盖的极大子区间即一个SCC。如下图。然后依然找a最大的点所在的SCC。

constexpr int N=1e5+2;
int a[N],b[N],p[N];
vector<int> ve[N];
bool vis[N];
void dfs(int u){
vis[u]=1;//printf("#dfs %d\n",u);
for(auto&& v:ve[u])if(!vis[v])dfs(v);
}
int main(){
for(int t=read();t--;){
int n=read(),maxi;
for(int i=0,maxa=0;i<n;++i){
a[p[i]=i]=read();
if(maxa<a[i])maxa=a[i],maxi=i;
ve[i].clear();
}
sort(p,p+n,[](int x,int y){return a[x]<a[y];});
for(int i=0;i<n-1;++i)ve[p[i]].push_back(p[i+1]);
for(int i=0;i<n;++i)b[p[i]=i]=read();
sort(p,p+n,[](int x,int y){return b[x]<b[y];});
for(int i=0;i<n-1;++i)ve[p[i]].push_back(p[i+1]);
memset(vis,0,n+1);
dfs(maxi);
for(int i=0;i<n;++i)putchar('0'^vis[i]);
puts("");
}
return 0;
}
F
按照题意直接构造,然后把所有答案存储在set甚至hash_table中,最后检测y是否被算出来过即可。
有效的答案的长度不会超过y的长度,这就为中间的计算确定了边界。
以上是因为数据范围有限(1e18)。数据范围大一点的话就得换高效算法了。
inline string rev(string t){
while(t.back() == '0') t.pop_back();
reverse(t.begin(), t.end());
return t;
}
string bin(int x){
return x?bin(x/2)+string(1,char(x&1^'0')):"";
}
signed main(){
//for(int i=1;i<=64;++i)cout<<bin(i)<<endl;
int x=read(),y=read();
set<string>used{bin(x)};
queue<string>q;
for(q.push(bin(x));!q.empty();){
string k=q.front();
q.pop();
if(k.size()>65)continue;
for(int i=0; i<2; i++){
string kk=rev(k+string(1,char('0'^i)));
if(!used.count(kk)){
used.insert(kk);
q.push(kk);
}
}
}
puts(used.count(bin(y))?"YES":"NO");
return 0;
}


