平面计算几何基础-by chenkehan @fdu

平面计算几何基础

计算几何要解决什么问题？

处理点、直线、线段、圆、多边形等几何图形的位置关系。

浮点数相关

存储方式：符号位F+指数位Z（阶码）+尾数位W

\(x=F\times W \times 2^{Z+Zmin}\)

对于double类型，F=1,W=11,Z=52，支持十进制15位精度的有效数字

浮点数的计算方式

加减法：把阶码较小的数的尾数右移两数阶码差值，然后尾数间进行加减运算

乘除法：尾数乘除，阶码加减

浮点误差的来源：加减法时较小数尾数右移时最后几位被截断，乘除法时尾数乘除的结果超过尾数位的部分被截断

浮点误差的处理：考察题目中输入数据产生的最小差值e1,自己算法运行过程中积累的最大差值e2,则所设计的eps应在e1与e2之间

减少浮点误差的几种方法：
1.避免非常接近的数的减法运算（或者绝对值接近的异号数的加法）
2.尽量避免绝对值相差过大的数之间的加减运算
3.减少运算次数
4.先乘后除

关于long double：当double用就行，不保证比double更精确

那么，即使使用了各种优化，仍然没法保证e1<e2该怎么办？

考虑全整数。整数更易于控制，且误差不会累计，更方便处理=0的corner case。（当然，需要进行三角函数运算时，整数就派不上用场了。不过我们还是可以在能用整数的阶段尽量多用整数。）

不过全整数也仅仅相当于一个64位尾数精度的浮点数类型而已，并没有比double精确很多。假如精度仍然不够，只能使用更高精度的数据类型了。（基本遇不到这种情况）

基本几何图形

尽量全整数，这意味着需要使用向量运算，而不是传统的解析式联立解方程。这里只考虑平面直角坐标系。

基本几何图形的存储

点/向量

点/向量：两个数x,y表示横纵坐标。用一个struct封装，重载掉加、减、点积、叉积运算，写好取长度、取极角等基本函数。

直线/线段

使用一个点p和一个向量v表示。对于线段，p表示线段起点，v表示起点到终点的向量。对于直线，p表示直线上任意一个点，v表示直线的方向向量。半平面的方向可以通过规定向量v的方向来表示，规定半平面区域在向量左侧或右侧。

圆

一个点O和一个数r表示半径和圆心

多边形

按顺时针方向存储每个点。

基本几何图形的基本操作

向量旋转

原向量\(\bold{v}=(x,y)\)，转换为极坐标表示\((l\cos\alpha,l\sin\alpha)\)。

设旋转角为\(\theta\)，则新向量\(\bold{v'}=(l\cos(\alpha+\theta),l\sin(\alpha+\theta))=(l(\cos\alpha\cos\theta-\sin\alpha\sin\theta),l(\sin\alpha\cos\theta+\cos\alpha\sin\theta))=(x\cos\theta-y\sin\theta,y\cos\theta+x\sin\theta)\)

判断点是否在半平面内

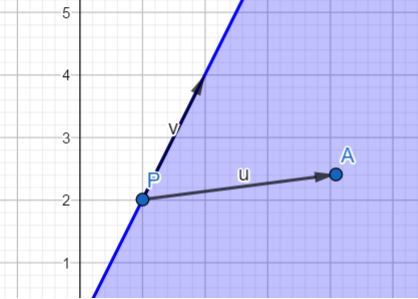
根据\((\bold{a}-\bold{p})\times \bold{v}\)的符号判断。

判断线段是否相交

转化为两个判断两点是否在直线两边的问题解决。

求直线交点

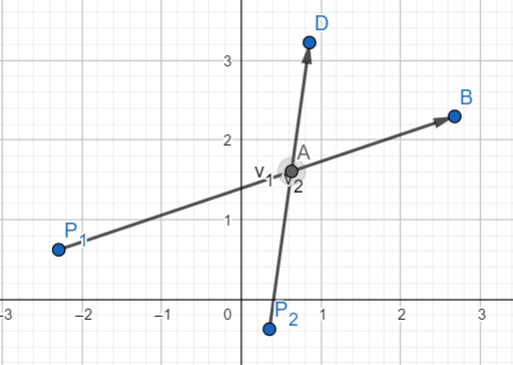
设\(\bold{a}=\bold{p_1}+t\bold{v_1}\)，则\((\bold{a}-\bold{p_2})\times \bold{v_2}=0\)

即\((\bold{p_1}-\bold{p_2}+t\bold{v_1})\times \bold{v_2}=0\)

则\(t=\frac{(\bold{p_2}-\bold{p_1})\times \bold{v_2}}{\bold{v_1}\times\bold{v_2}}\)

过一点作给定直线的垂线

把直线的方向向量旋转90度和给定点构造垂线。

垂足：求这两条直线的交点。

点到直线的距离：求给定点到垂足的距离。

中垂线：过线段中点作该线段的垂线

判断点与圆的位置关系

即判断点到圆心的距离与半径的大小关系。平方以实现全整数。

过三点构造圆

即求三角形外心，取中垂线交点。

判断直线与圆的位置关系

有过圆心、相交、相切、相离这几种情况，通过圆心到直线的距离和半径大小关系判断。

求直线与圆的交点

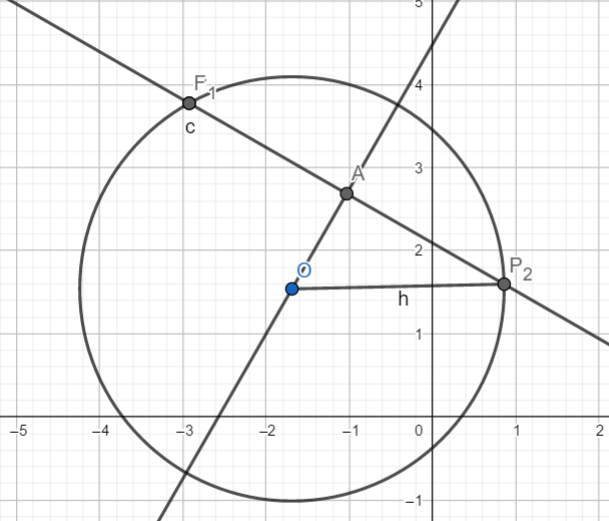
先过圆心作给定直线的垂线，记垂足为A。则\(|OP_1|=|OP_2|=\sqrt{r^2-|OA|^2}\)

设直线方向向量为v，令\(\bold{v'}=\frac{|OP_1|}{|\bold{v}|}\bold{v}\)，则\(\bold{p}=\bold{a}\plusmn\bold{v'}\)

判断两圆位置关系

有重合、同心、包含、内切、相交、外切、相离这几种情况。

先用圆心位置是否相同判掉重合和同心。设两圆半径为\(r_1,r_2(r_1\le r_2)\)，两圆心距离为\(d\)

\(d+r_1<r_2\)：包含

\(d+r_1=r_2\)：内切

\(d<r_1+r_2\)：相交

\(d=r_1+r_2\)：外切

\(d>r_1+r_2\)：相离

求两圆交点

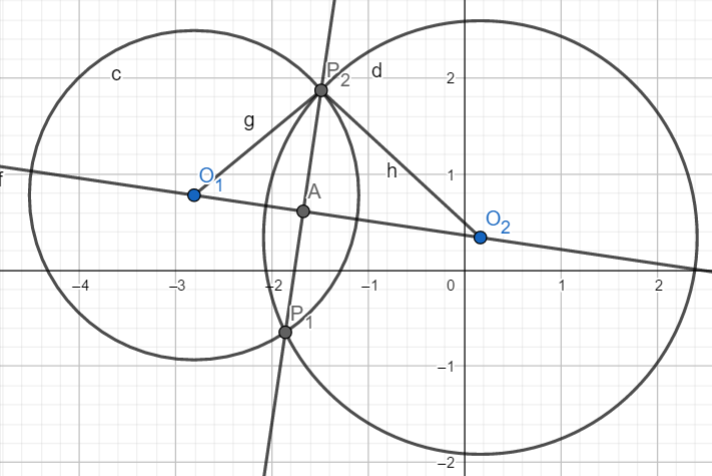
利用余弦定理得到\(\cos\angle PO_1O_2\)，转化为直线和圆交点问题。

判断点是否在多边形内

经典的pip问题。这里仅给出一个实现简单的做法：引射线法。

从给定点随便引出一条射线，计算射线与多边形边的相交次数。为奇数则在多边形内，否则在多边形外。

具体实现需要考虑到直线正好过多边形某个点或者正好与某条边重合的情况。这里有几种方式解决：

1.固定水平向右引直线，经过边上两个点则不算相交，与边上一个点重合则判断这个点是否是这条边纵坐标较大的点，是则记一次相交。

2.令射线的方向向量为(1,y),选定一个不会经过任何一个点的y。

3.给射线随机一个方向，认为随机的射线不会经过任何一个点。（这样没法全整数）

关于边际情况的处理

在判断关系时，有时会出现边际情况。即：判断点在直线哪边时正好点在直线上；直线和圆正好相切，只能求出一个交点，等等。假如题目保证不出现边际情况，那最好；假如可以全整数，那也行，只要直接判断是否=0就能区分出边际情况。糟糕的情况是没法全整数，又可能出现边际情况。这个时候就需要像前文讲浮点数中提到的那样设置eps，假如判别式的绝对值<eps，就认为处于边际情况。

经典算法

极角排序

问题

给定若干向量，要求把这些向量按照极角进行排序。

解决

我们先把极角强制在\([0,2\pi)\)范围内。很容易想到利用向量叉积来判断向量之间的顺序。然而，这只能判断旋转角与\(\pi\)的大小关系，并不能直接判断它的正负；而且也没法适应强制\([0,2\pi)\)这个条件，在两个向量旋转会跨过x轴正半轴时会出错。

因此，在比较的时候，我们先判断两个向量是否一个在\([0,\pi)\)，一个在\([\pi,2\pi)\)，是就强制给定顺序，否则使用向量叉积的正负来进行判断。

凸包构造

问题

给定n个点，求一个面积最小的包含这些点的凸集。

解决

显然这个凸集一定是个凸多边形，并且顶点一定在这n个点当中。这很好证明。那么我们只需要求出这n个点中哪些点会被选进凸包就可以了，这为我们存储凸包提供了便利。

解决构造凸包问题的经典算法有Graham扫描法和Andrew算法，这里仅介绍既快又好写的Andrew算法。

考虑分开来求凸包的上凸壳和下凸壳。首先把所有点按横坐标从小到大排序。显然，横坐标最小的点和横坐标最大的点都会在凸包的边界上。对于横坐标最小的几个点，其中纵坐标最小的点是下凸壳最左端的点，纵坐标最大的点是上凸壳最左端的点。对于横坐标最大的几个点也是一样。

先构造上凸壳。对于除了横坐标最小的点之外的点，按横坐标从小到大依次将它们加入凸壳（横坐标相同的点顺序任意）。使用单调栈维护凸壳即可。下凸壳也是一样。最后按逆时针的方向把它们合并。

单调栈维护凸壳的方法：

如图，已经维护好了ABCDE这个上凸壳，现在要加入点F。显然，新的凸壳应该是ABCF。那么，要怎么实现这个增量的过程呢？

凸包相邻的三个点A,B,C一定满足条件：\(\overrightarrow{BC}\times\overrightarrow{AB}>0\)。从右往左考虑原凸壳中的每个点\(P_n\)在加入\(P_{n+1}\)后\((P_{n-1},P_n,P_{n+1})\)三个点是否满足这个条件，假如不满足，就将\(P_n\)从凸包中删去，继续考虑\(P_{n-1}\)是否需要删去，直到原凸壳中只剩一个点或者条件不满足。能被删去的点一定是从右到左连续的一段，因此算法的正确性得到证明。由于每个点只会加入一次和最多删除一次，因此时间复杂度为\(\Theta(n)\)

由于算法需要排序，时间复杂度的瓶颈在排序上。假如使用基于比较的排序算法，则Andrew算法整体时间复杂度为\(\Theta(n\log n)\)。

在实际的代码中，只需要以横坐标为第一关键字，纵坐标为第二关键字排序就可以解决横坐标相同的问题。

旋转卡壳

问题

二维平面上给定n个点，求距离最大的两个点。

解决

考虑到距离最大的两个点一定在凸包上，那么问题就等价于求凸包的直径。假如是直接枚举两个点，则复杂度并没有改进。考虑对于每个点，距离它最远的点是哪个点。那么逆时针地枚举每个点，是不是距离它距离最大的点一定也是逆时针地在移动呢？

答案是肯定的。然而，凸包上逆时针方向每个点关于一个点的距离并不是一个单峰函数，无法直接判断一个点是否是距离给定点最远的点。这就导致我们仍然无法依靠双指针的方法来优化复杂度。

虽然凸包上逆时针方向每个点关于给定点的距离不是单峰函数，但是对于另外一个命题却有更优秀的结果。即：凸包上逆时针方向每个点关于凸包上一条边所在直线的距离一定是个单峰函数。显然，逆时针地枚举凸包的边，距离其所在直线最远的点也是逆时针移动的。同时又有另一个正确的命题：对于凸包上每条边\(AB\)，取距离\(AB\)所在直线最远的点\(C\)（如果有多个，则任取），则直径一定在这些\(AC\)与\(BC\)中取到。

利用这两个命题，我们可以写出如下算法：逆时针枚举每条边，再维护一个指针指向距离这条边所在直线最远的点，每次把答案与这个点到边的两个端点的距离取max。判断两个点到一条边所在直线距离的大小关系可以用同底三角形的面积来比较，就转化为叉积大小的比较。算法时间复杂度为\(\Theta(n)\)，总复杂度瓶颈在构造凸包上。

实际上，这种在凸包上维护双指针的思想是应用很广泛的。例如，可以用类似的做法解决点集的最小矩形覆盖问题。

半平面交

问题

给定若干个半平面，求它们的交。

解决

由于半平面是凸集，其交也应该是个凸集。假如这些半平面的交是一个有限区域，则一定是一个凸包（或者交为空）。假如半平面交是一个无限区域，处理就比较麻烦。考虑人工添加四个半平面构成的足够大的外边框来把半平面限制在有限区域，也方便判断半平面交是否有限。

朴素的想法是求出这些半平面两两之间的交点，再检验这些交点有哪些不被其他某个半平面包含，就将这些点排除掉，最后剩下的点就是半平面交的顶点。但是\(\Theta(n^2)\)的时间复杂度显然不能接受。

考虑增量的想法。显然，在最终的半平面交构成的凸包中，相邻的边的方向向量一定是按极角序排列的。考虑按方向向量极角序逆时针一个个添加半平面（遇到方向一样的半平面，就取约束条件最严格的那个），维护当前添加的所有半平面围成的开口凸壳的逆时针方向顶点序列和有效半平面（构成凸包某条边的半平面）序列。每次新添加半平面时，检查目前凸壳的所有顶点是否被这个半平面包含，若不包含就将其删去。先不考虑删去顶点的后续维护问题，我们有这样一个结论：不被当前半平面包含的顶点一定是从顶点序列头开始的一段和从顶点序列尾开始的一段共两段（可能为空的）连续序列。这个结论等价于给凸包新增一个半平面约束，此半平面只会对包含方向向量极角序相邻的两条边的交点的顶点连续段产生影响，则进行半平面交时也只需要考虑极角序相邻的半平面之间的互相约束。因此，使用单调队列可以线性地维护这个凸壳，删除队列两端的顶点时也删除队列两端的半平面。值得注意的是，在加入所有半平面后，我们只考虑了队列尾部的半平面对队列头部的顶点的约束，没有考虑队首半平面对队列尾部顶点的约束，且目前顶点数比有效半平面数少一个，凸包并没有封口。因此，最后还需要检查一遍弹出队尾不在队首半平面内的交点，并求出队首半平面与队尾半平面的交点来给凸包封口。最小a

由于有点难以理解，这里给出我的代码。s是半平面数组，qs是队列中半平面的编号，qp是凸包顶点序列。isin(a,b)是判断点a是否在半平面b中的函数，inter(a,b)是求出a,b两条直线的交点的函数。

h=t=1; qs[1]=1;
For(i,2,lens)
{
    while(h<t&&!isin(qp[t],s[i]))t--;
    while(h<t&&!isin(qp[h+1],s[i]))h++;
    qs[++t]=i;
    qp[t]=inter(s[qs[t-1]],s[i]);
}
while(h<t&&!isin(qp[t],s[qs[h]]))t--;
qp[h]=inter(s[qs[h]],s[qs[t]]);

注意这里必须要先弹出队尾再弹出队首，否则在把队列删到只剩一个元素的情况会出现问题。

最后假如凸包的顶点数量小于3，则半平面交的结果为空。