单调队列:从滑动窗口到NOIp2016-蚯蚓
* 先附上网址
https://www.luogu.com.cn/problem/P1886
一道经典题目了。之前就做过(2019年山东省夏令营,2019-07-20 09:14,看来是在礼堂听课时做的)
闲话不多说就是单调队列,一种数据结构,维护两个方面:

为了懒,当然用stl:deque啦(其实是head==tail还是head>tail搞不清楚)
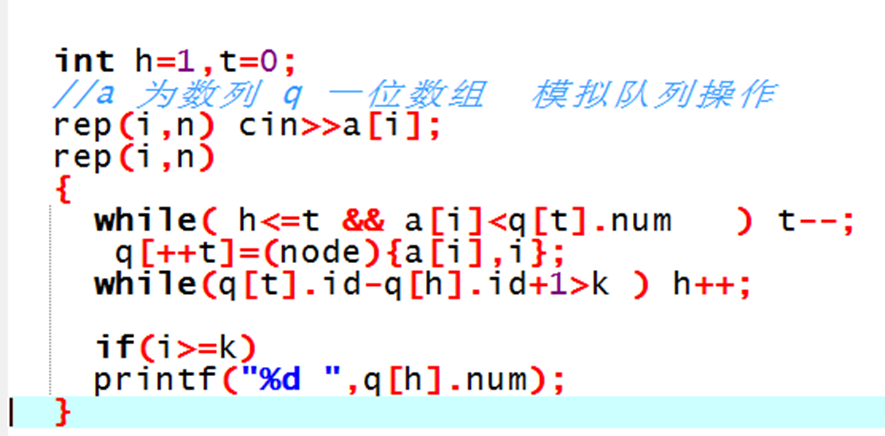
不过用st表也能AC,需要注意卡常数,代码如下:
#include<cstdio>
#include<cmath>
#define min(a,b) (a<b?a:b)
#define max(a,b) (a>b?a:b)
int n,k,a[1000006],st[1000006][22];
inline int read()//不快读的话过得很勉强,快读就比较轻松。另外不要引用isdigit()函数,会变慢
{
int x=0,f=1;char ch=getchar();
while (ch>'9'||ch<'0'){if (ch=='-') f=-1;ch=getchar();}
while (ch>='0'&&ch<='9'){x=x*10+ch-48;ch=getchar();}
return x*f;
}
int main(){
scanf("%d%d",&n,&k);
for(int i=1;i<=n;++i){
//scanf("%d",a+i);
st[i][0]=read();
}
for(int j=1,maxx;j<=20;++j){
maxx=n-(1<<j)+1;
for(int i=1;i<=maxx;++i)
st[i][j]=min(st[i][j-1],st[i+(1<<j-1)][j-1]);
}
int len=log2(k);//直接用此函数的话,已试验,输入整数时无误差
for(int i=1;i<=n-k+1;++i)
printf("%d ",min(st[i][len],st[i+k-(1<<len)][len]));//其实是(i+k-1)-(1<<len)+1
printf("\n");
for(int j=1,maxx;j<=20;++j){
maxx=n-(1<<j)+1;
for(int i=1;i<=maxx;++i)
st[i][j]=max(st[i][j-1],st[i+(1<<j-1)][j-1]);
}
for(int i=1;i<=n-k+1;++i)
printf("%d ",max(st[i][len],st[i+k-(1<<len)][len]));
return 0;
}
接下来是蚯蚓这道题
https://www.luogu.com.cn/problem/P2827
/**
* 蛐蛐国里现在共有 n 只蚯蚓( n 为正整数)。
* 每只蚯蚓拥有长度,我们设第 i 只蚯蚓的长度为 a[i]
* (i=1,2,...,n)
* 并保证所有的长度都是非负整数
* (即:可能存在长度为 0 的蚯蚓)。
*//**
* 每一秒,神刀手会在所有的蚯蚓中,
* 准确地找到最长的那一只(如有多个则任选一个)
* 将其切成两半。
* 神刀手切开蚯蚓的位置由常数 p
* (是满足 0 < p < 1 的有理数)
* 决定,设这只蚯蚓长度为 x,
* 神刀手会将其切成两只长度分别为
* ⌊px⌋ 和 x - ⌊px⌋ 的蚯蚓。
* 特殊地,如果这两个数的其中一个等于 0,
* 则这个长度为 0 的蚯蚓也会被保留。
* 此外,除了刚刚产生的两只新蚯蚓,
* 其余蚯蚓的长度都会增加 q(是一个非负整常数)。
*/
附上ckw大佬的分析(也是2019年夏令营的)

那么思想的话已经很明显了。正解也很多,文章最后贴一个正解做法(我们教练写的)。这里给一个骗分的做法:
NOIp部分分给的非常足!且数据一般不会出现极限数据,必须卡常之类的
这就给我们快速拿 部分分 提供了可乘之机
我们快速写一个不是正解但是一定对的代码然后疯狂卡常,如下:
考虑到每次取最大蚯蚓,且不断插入/删除,我们用一个优先队列来维护
其他的就是照着题面模拟了。需要注意的是每次插入新的蚯蚓时要减去time×q以“拉平”,
换言之,其他蚯蚓都少加了time×q,切的这条蚯蚓切的时候是真实的长度,切后要变回“虚假”的长度
其他的按照体面输入输出就完了。开不开O2优化都是85分,优化作用也有限。
#include<cstdio>
#include<queue>
using namespace std;
int _X,_F,CH;
inline int read(){//read
_X=0;_F=1;CH=getchar();
while(CH>57||CH<48){if(CH=='-')_F=-1;CH=getchar();}
while(CH>=48&&CH<=57){_X=_X*10+CH-48;CH=getchar();}
return _X*_F;
}
priority_queue<int/*,vector<int>,greater<int> */>pq;
int n,m,q,u,v,t/*,a[100005]*/;//含义见题目
int longest,shorter;//变量名起的长一点便于理解
int main(){
n=read();m=read();q=read();u=read();v=read();t=read();
for(int i=1;i<=n;++i)
{
//a[i]=read();
pq.push(read());
}
for(int time=1;time<=m;++time)
{
longest=pq.top();pq.pop();
longest+=(time-1)*q;//本轮他并没有变长
if(time%t==0)printf("%d ",longest);
shorter=longest*(long long)u/v;//这个long long常数很大,但是必须
pq.push(shorter-time*q);pq.push(longest-shorter-time*q);
//写这篇文章时我想到了把time*q存起来,但是该拿的85分到手了,剩下几个点真的没什么用
}
putchar('\n');
int addlen=m*q;//<2^31
for(int i=1;i<=n+m;++i)
{
if(i%t){pq.pop();continue;}
longest=pq.top();pq.pop();
printf("%d ",longest+addlen);
}
return 0;
}
这是一份正解,三个单调队列,含义如ckw所述。题解满大街都是,贴个我们教练的:

# include<bits/stdc++.h>
#define rep(i,n) for(int i=1;i<=n;++i)
using namespace std;
inline int read()
{
int x=0,f=1;
char ch;ch=getchar();
while(ch<48 ||ch>57){if(ch=='-') f=-1;ch=getchar(); }
while(ch>=48&&ch<=57) {x=x*10+ch-48;ch=getchar();}
return x*f;
}
const int N=1e5+5;
const int M=1e7;
int a[3][M],cut[M],h[3],t[3];//a[0] 原数列 a[1] 砍断后长的段 a[2]砍断后短的段
// cut [] 记录被砍断的蚯蚓 h[0] h[1] h[2] 代表 a[0] a[1] a[2]头指针 t[]分别是尾指针
int n,m,q,u,v,T,inf;
bool cmp(int &a,int &b) {return a>b;}
int main()
{ //freopen("in.txt","r",stdin);
cin>>n>>m>>q>>u>>v>>T;
for(int i=0;i<=2;++i) rep(j,M)a[i][j]=-1e9;
inf=-1e9;
h[0]=h[1]=h[2]=1; cut[0]=0;
rep(i,n) a[0][i]=read();
sort(a[0]+1,a[0]+1+n,cmp);// 首先让a[0] 从大到小 有序
double per=u*1.0/v;
rep(i,m)// 开始砍蚯蚓
{
int temp,maxn;
if(a[0][h[0]]>=a[1][h[1]]) maxn=a[0][h[0]],temp=0;
else maxn=a[1][h[1]],temp=1;
if(a[2][h[2]]>maxn) maxn=a[2][h[2]],temp=2;
// 找到a[0] a[1] a[2] 队首最大的 就是 应该被砍的蚯蚓
h[temp]++;//被砍的蚯蚓被弹出队首
if(i%T==0)cut[++cut[0]]=maxn+(i-1)*q;//被砍的蚯蚓应当加上增长补偿,每一秒都增长q
// 接下来把砍断的蚯蚓 按大小存在a[1] a[2] 队列
int small=(maxn+(i-1)*q)*per,big=maxn+(i-1)*q-small;
if(big<small) swap(big,small);
a[1][++t[1]]=big-i*q,a[2][++t[2]]=small-i*q;
}
//按要求输出 事后我想cut数组也许没有必要 直接输出即可
rep(i,cut[0]) cout<<cut[i]<<" "; cout<<endl;
int left=(n+m)/T,cnt=0;
// 后来身负洪荒之力人来了 蚯蚓不在增长 只需要把序列输出即可
while(left)
{
int temp,maxn=inf;
if(a[0][h[0]]>=a[1][h[1]]) maxn=a[0][h[0]],temp=0;
else maxn=a[1][h[1]],temp=1;
if(a[2][h[2]]>=maxn) maxn=a[2][h[2]],temp=2;
h[temp]++;
if(++cnt%T==0)cout<<maxn+m*q<<" ",left--;
}
return 0;
}
还有一位同学因常数过大被卡所以一定快读:
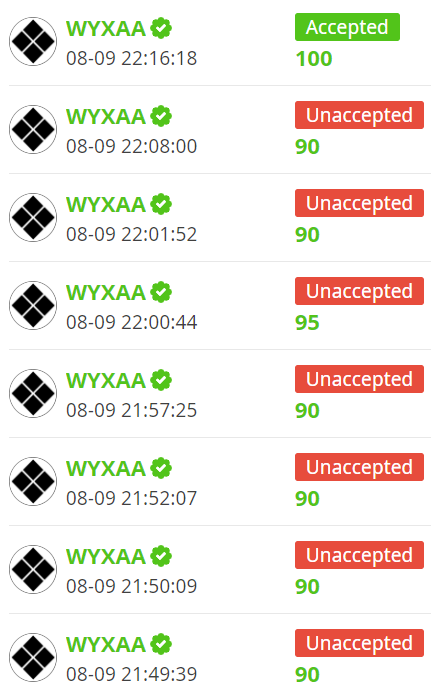
文末总结:
一些看似高级的题目其实可能有简单(吗?)的做法,尤其是单调队列,好几次出现了
所以还是那句话,基础算法灵活掌握。
另外就是ckw教的经验吧,先考虑部分分的限制条件,不行就先自己加一个,在这种受限的背景下题目还会含有什么限制条件,
再推广到更高分看是不是还成立。我觉得部分分就挺香的了


