ABC371F Takahashi in Narrow Road 题解 模拟+线段树

题目链接：https://atcoder.jp/contests/abc371/tasks/abc371_f

题目大意：

有一条向东和向西延伸的道路，\(N\) 个人在这条道路上。道路从一个称为原点的点向东和向西无限延伸。

第 \(i\) 个人 \((1\leq i\leq N)\) 最初位于原点东侧距离原点 \(X_i\) 米处。

这些人可以沿着道路向东或向西移动。具体来说，他们可以执行以下移动任意次数。

选择一个人。如果目的地没有其他人，则将选择的人向东或向西移动 \(1\) 米。

注：这里说的目的地指的是，如果这个人要向东移动 \(1\) 米，则目的地就是东边 \(1\) 米的地方；如果这个人要向西移动 \(1\) 米，则目的地就是西边 \(1\) 米的地方。

他们总共有 \(Q\) 个任务，第 \(i\) 个任务 \((1 \leq i \leq Q)\) 描述如下：

第 \(T_i\) 个人到达坐标 \(G_i\)。

找出依次完成所有 \(Q\) 个任务所需的最小总移动次数。

解题思路：

首先本题中我们定义的 “连通块” 指的是一段挨着的人（即这一段错了最左边那个人以外，每个人的坐标都比它左边那个人大 \(1\)）。

以下图为例：

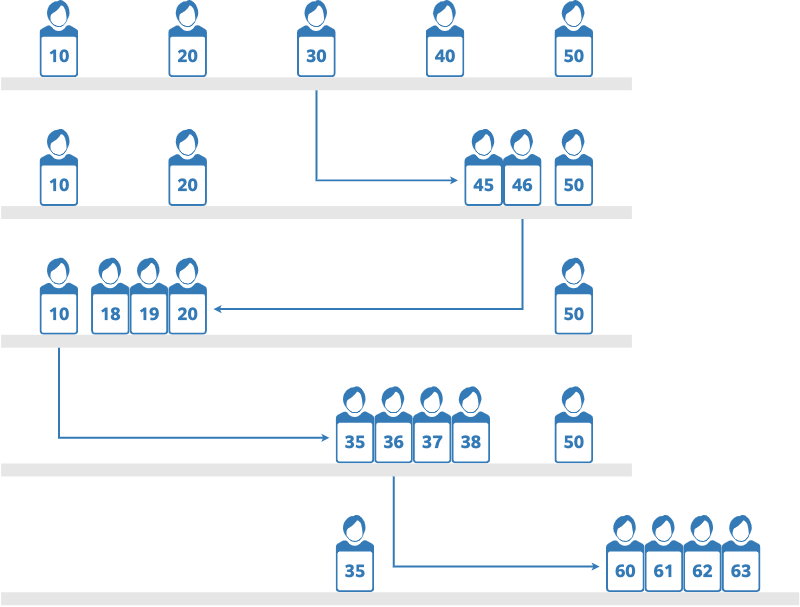
• 第一阶段：每个人都属于同一个连通块；
• 第二阶段：第 \(1\) 个人单独一个连通块，第 \(2\) 个人单独一个连通块，第 \(3 \sim 5\) 个人属于同一个连通块；
• 第三阶段：第 \(1 \sim 4\) 个人属于同一个连通块，第 \(5\) 个人单独一个连通块；
• 第四阶段：仍然是第 \(1 \sim 4\) 个人属于同一个连通块，第 \(5\) 个人单独一个连通块；
• 第五阶段：第 \(1\) 个人单独一个连通块，第 \(2 \sim 5\) 个人属于同一个连通块。

在整体的 \(Q\) 次移动中，每次移动：

• 最多有 \(n\) 个连通块合并成一个连通块；
• 最多有 \(1\) 个连通块被拆分为两个连通块。

考虑 暴力去合并与拆分连通块？\(\Rightarrow\) 其实是可行的。

因为每次操作最多（通过拆分）增加一个连通块，初始时最多 \(n\) 个连通块，而最终合并能够得到的最终的连通块的个数最少是一个。所以，我们实际上合并连通块的次数不超过 \(n+q-1\) 次。虽然一次合并操作就可能合并 \(n-1\) 次连通块（看上去很吓人），但是实际整个过程中，合并和拆分连通块的次数是 \(O(n+q)\)，均摊下来次数还是比较少的。

而且在代码实现时，我们可能是同时将一段区间的多个连通块合并成一个连通块，这样实际的合并次数就更少了。

在实现时，我们用线段树维护了一个信息，那就是每个人所在的连通块中最左边那个人的编号。在线段树中支持的操作有两个：

• bl(p)：（单点查询）查询第 \(p\) 个人所在的连通块中最左边那个人的编号；
• merge_people(l, r)：（区间更新）将区间 \([l, r]\) 合并成一个连通块。

同时我们实时更新每个区间最左边那个人（第 \(p\) 个人）的位置 \(x[p]\)。\(\Rightarrow\) 这很关键，因为以 \(p\) 为最左边的人的连通块中其他人的位置都是由 \(p\) 决定的。

如果 \(q\) 和 \(p\) 属于同一个连通块，\(x[p]\) 是第 \(p\) 个人此时实际所在的位置，则 \(q\) 所在的位置应为 \(x[p] + q - p\)（因为同一个连通块里的人是挨着的）。具体实现时，我开了一个 get_pos(p) 函数获取第 \(p\) 个人的位置。

题目里面是第 \(T_i\) 个人移动到坐标 \(G_i\)。我在分析移动的时候将其表示为第 \(p\) 个人移动到坐标 \(G\)。

所限我们一个通过 get_pos(p) 函数获得第 \(p\) 个人当前（即移动前）所在的坐标 \(P\)。

• 如果 \(P = G\)（起点等于中点），不需要移动；
• 如果 \(P \lt G\)，需要向右移动；
• 如果 \(R \gt G\)，需要向左移动。

所以接下来我们分 向右移动 和 向左移动两种情况进行分析。

向右移动

如果 \(p\) 向右移动，\(p\) 和他左边的那个人就差分开来了，第 \(1 \sim p-1\) 所属的连通块的信息不变（所以不需要额外处理第 \(p\) 个人左边的那些人的归属信息）；同时，以 \(p\) 为左端点肯定向右有连续的一段数字在向右移动后都归属于 \(p\)，对于第 \(p\) 个人右边的第 \(q\) 个人，因为 \(p\) 在移动后到达的位置是 \(G\)，而 \(q\) 如果和 \(p\) 在同一个连通块，则 \(q\) 最终的位置肯定是在位置 \(G + q - p\) 处，所以我们可以通过判断 \(q\) 当前所在的坐标是否 \(\le G+q-p\) 来判断 \(q\) 是否在 \(p\) 移动后和 \(p\) 属于同一个连通块。\(\Rightarrow\) 然后我们就可以通过二分查找找到最右边的那个和 \(p\) 属于同一个连通块的人 —— 设他是第 \(q\) 个人。

此时，将 \([p, q]\) 合并成一个连通块即可。

这里要注意，如果 \(q \lt n\)，则合并前后 \(q\) 和 \(q+1\) 肯定不属于同一个连通块（不然二分找到的就是 \(q+1\) 或者更后面的数而不是 \(q\) 了）。

向左移动

向左移动时，我们也可以二分得到最左边的那个和 \(p\) 属于同一个连通块的人（设它是第 \(pp\) 个人），则 \([pp, p]\) 合并成一个连通块。

同时要注意，第 \(p\) 个人和第 \(p+1\) 个人在移动前可能是属于同一个连通块的，当 \(p\) 向左移动后，第 \(p+1\) 个人开始的一些人，他们所在的连通块的最左边的人会变为第 \(p+1\) 个人。

所以我们要在二分查找一下移动前 \(p\) 右边的那些人中最右边的那个和 \(p\) 属于同一个连通块的人，设为第 \(q\) 个人，如果 \(q \lt p\)，则将 \([p+1, q]\) 合并成一个新的连通块。

这样我们就实时更新了位置。

但是我们并没有计算移动次数。

所以接下来最关键的就是 cal(l, r) 函数。

它用于计算 \([l, r]\) 这些人的坐标之和。

我的 cal(l, r) 函数保证 \([l, r]\) 范围内是若干个完整的连通块（即 \(l\) 是它所在连通块最左边那个人，\(r\) 是他所在连通块最右边那个人）。

对于一个连通块 \([l, r]\)，如果我们知道 \(l\) 的坐标 \(x[l]\)，那么 \([l, r]\) 范围内所有人的坐标总和是一个等差数列之和，即 \((x[l] + x[l] + r - l) \times (r - l + 1) / 2\)。

我们只计算每次移动前后变化过的完整区间的坐标和，所以虽然每次移动都会调用 cal 函数，但是 cal 函数实际计算的完整区间的总数也是 \(O(n + q)\) 数量级的。

• 如果是往右移动（坐标整体变大），移动后 cal(l, r) 的值减去移动前 cal(l, r) 的值其实就是 \([l, r]\) 范围内坐标的增量，即最少移动次数；
• 如果是往右移动（坐标整体变小），移动前 cal(l, r) 的值减去移动后 cal(l, r) 的值其实就是一勺移动次数。

按照这个逻辑就可以得到最少移动次数总和了。

示例程序：

#include <bits/stdc++.h>
using namespace std;
const int maxn = 2e5 + 5;
int n, q, x[maxn];
long long ans;

int tr[maxn<<2];
#define lson l, mid, rt<<1
#define rson mid+1, r, rt<<1|1
void push_up(int rt) {
    // ...
}
void push_down(int rt) {
    if (tr[rt]) {
        tr[rt<<1] = tr[rt<<1|1] = tr[rt];
        tr[rt] = 0;
    }
}
void build(int l, int r, int rt) {
    if (l == r) {
        tr[rt] = l;
        return;
    }
    int mid = (l + r) / 2;
    push_down(rt);
    build(lson), build(rson);
    push_up(rt);
}
int query(int p, int l, int r, int rt) { // 查询第 p 个人归属于哪个人
    if (l == r)
        return tr[rt];
    int mid = (l + r) / 2;
    push_down(rt);
    return (p <= mid) ? query(p, lson) : query(p, rson);
}
int bl(int p) {     // 查询第 p 个人归属于哪个人
    return query(p, 1, n, 1);
}
void update(int L, int R, int p, int l, int r, int rt) { // [L, R] 都归 p
    if (L <= l && r <= R) {
        tr[rt] = p;
        return;
    }
    int mid = (l + r) / 2;
    push_down(rt);
    if (L <= mid) update(L, R, p, lson);
    if (R > mid) update(L, R, p, rson);
    push_up(rt);
}
void merge_people(int l, int r) {   // 将 [l, r] 合并成一个连通块
    update(l, r, l, 1, n, 1);
}

int get_pos(int p) { // 获得第 p 个人当前实际所在的位置
    return x[ bl(p) ] + p - bl(p);
}

long long cal(int l, int r) {
    long long res = 0;
    int p = r;
    while (p >= l) {
        int pp = bl(p);
        assert(bl(pp) == pp);
        res += (long long) (get_pos(pp) + get_pos(p)) * (p - pp + 1) / 2;
        p = pp - 1;
    }
    assert(p == l - 1);
    return res;
}

void go_right(int p, int G) {
    // q 对应最右边一个和 p 挨着的人
    int l = p, r = n, q;
    while (l <= r) {
        int mid = (l + r) / 2;
        if (G + mid - p >= get_pos(mid))
            q = mid, l = mid + 1;
        else
            r = mid - 1;
    }
    int pp = bl(p);
    ans -= cal(pp, q);
    x[p] = G;
    merge_people(p, q);
    ans += cal(pp, q);
}

void go_left(int p, int G) {
    // pp对应最左边一个和 p 挨着的人
    int l = 1, r = p, pp;
    while (l <= r) {
        int mid = (l + r) / 2;
        if (G + mid - p <= get_pos(mid))
            pp = mid, r = mid - 1;
        else
            l = mid + 1;
    }
    // q对应（向左移动前）最右边一个和 p 挨着的人（没有则 q = -1）
    int q = p;
    l = p+1, r = n;
    while (l <= r) {
        int mid = (l + r) / 2;
        if (bl(mid) <= p)
            q = mid, l = mid + 1;
        else
            r = mid - 1;
    }
    ans += cal(pp, q);
    if (p < q) {
        x[p+1] = get_pos(p+1);
        merge_people(p+1, q);
    }
    x[pp] = G + pp - p;
    merge_people(pp, p);
    ans -= cal(pp, q);
}

int main() {
    scanf("%d", &n);
    for (int i = 1; i <= n; i++)
        scanf("%d", x+i);
    build(1, n, 1);
    scanf("%d", &q);
    while (q--) {
        int p, G; // 第 p 个人走到下标 G
        scanf("%d%d", &p, &G);
        int P = get_pos(p);
        if (P < G)
            go_right(p, G);
        else if (P > G)
            go_left(p, G);
    }
    printf("%lld\n", ans);
    return 0;
}