洛谷P4159 [SCOI2009] 迷路 题解 矩阵快速幂/拆点

题目链接：https://www.luogu.com.cn/problem/P4159

题目大意：
给你一个包含 \(n\) 个点的有向图以及一个邻接矩阵，求从 \(1\) 号点到 \(n\) 号点的长度为 \(t\) 的路径有多少种。有向边长度 \(\le 9\)。

解题思路：

如果每条边的长度都为 \(1\) ，则直接可以用矩阵连乘做。但是没有

考虑到每条边的长度都不超过 \(9\)，所以考虑把每条边都拆分成若干条长度为 \(1\) 的边，这就需要额外地添加一些点。

具体地说（为了方面起见，我把一开始的 \(n\) 个点的编号从 \(0\) 开始，即 \(0,1,2, \cdots, n-1\) 号节点）：

对于节点 \(i(0 \le i \lt n)\)，将其拆分成 \(i \cdot 9, i \cdot 9 + 1, i \cdot 9 + 2, \cdots , i \cdot 9 + 8\) 这 \(9\) 个点。
然后对于所有 \(1 \le j \lt 9\)，连一条 \(i \cdot 9 + j \rightarrow i \cdot 9 + j - 1\) 的边（边权为 \(1\)）。
然后，如果从节点 \(x\) 到节点 \(y\) 有一条边权为 \(q\) 的边，则从 \(x \cdot 9\) 向 \(y \cdot 9 + q - 1\) 连一条边（边权为 \(1\)）。
然后就相当于将原始的图转变成了一个边权为 \(1\) 的有向图了。

具体如下图所示：

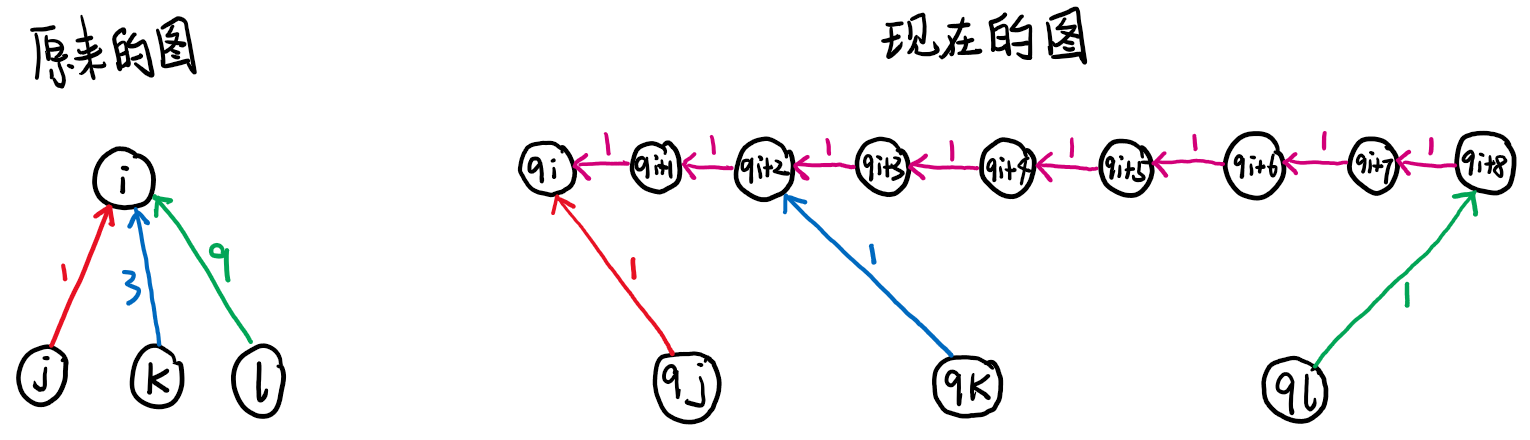
然后在这个邻接矩阵上做矩阵快速幂就可以了。

示例代码：

#include <bits/stdc++.h>
using namespace std;
const int maxn = 110, MOD = 2009;
struct Matrix {
    int n, a[maxn][maxn];
    Matrix operator * (Matrix b) const {
        Matrix c;
        c.n = n;
        memset(c.a, 0, sizeof(c.a));
        for (int i = 0; i < n; i ++)
            for (int j = 0; j < n; j ++)
                for (int k = 0; k < n; k ++)
                    c.a[i][j] = (c.a[i][j] + a[i][k] * b.a[k][j]) % MOD;
        return c;
    }
    Matrix operator ^ (int m) const {
        Matrix b, c;
        b.n = c.n = n;
        memcpy(b.a, a, sizeof(a));
        memset(c.a, 0, sizeof(c.a));
        for (int i = 0; i < n; i ++) c.a[i][i] = 1;
        while (m) {
            if (m % 2) c = c * b;
            b = b * b;
            m /= 2;
        }
        return c;
    }
} a;
int n, t;
char s[11];
int main() {
    cin >> n >> t;
    a.n = n * 9;
    memset(a.a, 0, sizeof(a.a));
    for (int i = 0; i < n; i ++) {
        for (int j = 1; j < 9; j ++)
            a.a[i*9+j][i*9+j-1] = 1;
    }
    for (int i = 0; i < n; i ++) {
        cin >> s;
        for (int j = 0; j < n; j ++) {
            int num = s[j] - '0';
            if (num) {
                int x = j * 9 + num - 1;
                a.a[i*9][x] = 1;
            }
        }
    }
    cout << (a ^ t).a[0][(n-1)*9] << endl;
    return 0;
}