树堆(Treap)学习笔记 2020.8.12
如果一棵二叉排序树的节点插入的顺序是随机的,那么这样建立的二叉排序树在大多数情况下是平衡的,可以证明,其高度期望值为 \(O( \log_2 n )\)。即使存在一些极端情况,但是这种情况发生的概率很小。而且这样建立的二叉排序树的操作很方便,不必像伸展树那样通过伸展操作来保持数的平衡,也不必像 AVL 树、红黑树等结构那样,为了达到平衡而进行各种复杂的旋转操作。变成复杂度低了,正确率就很高,这对有限的竞赛时间和紧张的竞赛考场是很重要的。
Treap 就是一种满足堆的性质的二叉排序树。在保持二叉排序树基本性质不变的同时,为每一个节点设置一个随机的权值,权值满足堆的性质,其结构和效果相当于按随机顺序插入节点而建立的二叉排序树。它的实现简单,支持伸展树的大部分操作,而且效率高于伸展树。
“Treap”一词是由“Tree”和“Heap”而来。Treap本身是一棵二叉排序树,它的左子树和右子树也分别是一棵Treap。
和一般的二叉排序树不同的是,Treap记录了一个额外的数据域 —— 优先级。Treap在以关键字构成二叉排序树的同时,优先级还满足堆的性质(这篇随笔假设采用小根堆)。但是,Treap和堆有一点不同:堆必须是完全二叉树,而Treap并不一定要求是。
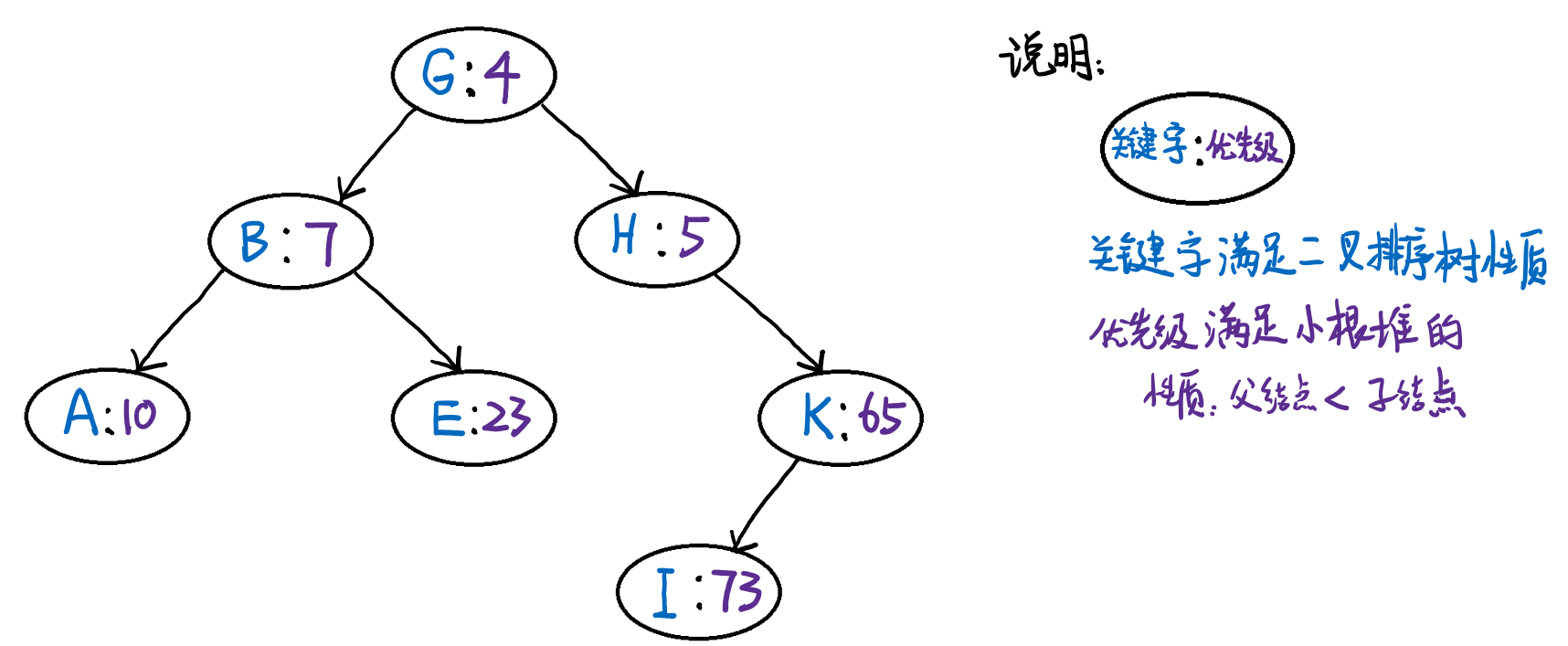
如图所示就是一个 Treap 结构,其按关键字中序遍历的结果是:ABEGHIK,而且优先级满足小根堆。
1. Treap的基本操作
让 Treap 同时满足两个性质的具体做法是:首先让它满足二叉排序树的性质,再通过旋转操作(左旋或右旋),在不破坏二叉排序树性质的同时满足堆的性质。Treap 旋转操作主要通过操作某个父节点和它的一个子节点,让子节点上去,父节点下来。
下图是 Treap 的左旋和右旋操作的示意图:
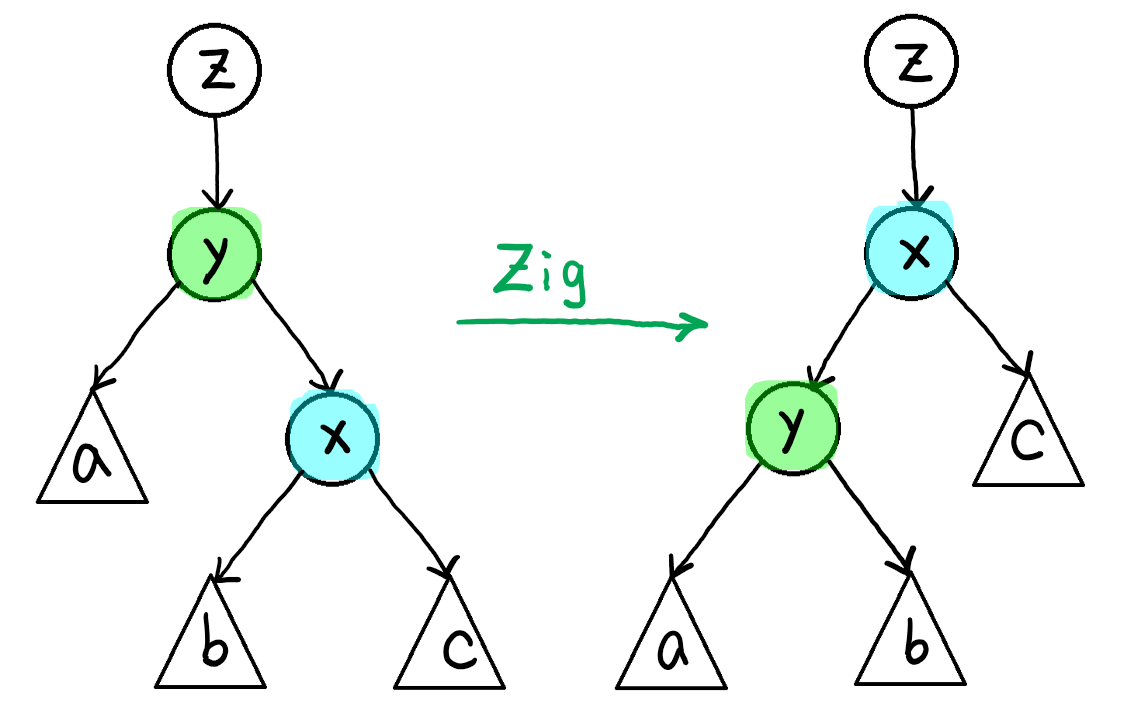
Treap的左旋操作

Treap的右旋操作
(一个疑惑:为什么Splay的左旋叫Zag,右旋叫Zig;而Treap的左旋叫Zig,右旋叫Zag?)
在 Zig 和 Zag 操作中,可以看到 \(a,b,c,x,y\) 之间的大小关系没有发生改变。
由于是二叉搜索树,满足根节点的关键字 \(\gt\) 左子树;\(\lt\) 右子树,所以
对于上图中的左旋(Zig)操作,翻转前
(其中 \(A,B,C\) 分别表示以 \(a,b,c\) 为根节点的子树中的所有元素)
翻转后仍然满足这个性质。
对于上图中国的右旋(Zag)操作,翻转前
翻转后仍然满足这个性质。
通过左旋和右旋两种旋转操作,一个节点可以在Treap中自由地上下移动,而且节点的上下移动很容易和堆节点的上调和下调对应起来。下面介绍Treap的一些基本操作。
1. 查找、求最大值、求最小值
这三个操作和二叉排序树的做法一样,但是由于Treap的随机化结构,可以证明在Treap中查找、求最大值、求最小值的时间复杂度都是 \(O(h)\) 的,其中,\(h\) 表示树的高度。
2. 插入
先给节点随机分配一个优先级,然后和二叉排序树的节点插入一样,把要插入的节点插入到一个叶子上,然后维护堆的性质,即如果当前节点的优先级比根小就旋转(如果当前节点是根的左二子就右旋,如果当前节点是根的右儿子就左旋)。
假设要插入的数依次为 \(1,2,3,4,5,6\),通过随机函数得到的优先级分别为 \(10,22,5,80,37,45\),则依次插入节点的过程如下:
插入 \(1\) 和 \(2\) 时都没有影响堆的性质,所以不需要进行旋转维护。
\((3:5)\) 插入后,由于 \(5\) 比 \(22\)、\(10\) 都小,所以要进行两次旋转操作,把 \((3:5)\) 调整到最上面,保证了优先级符合堆性质。
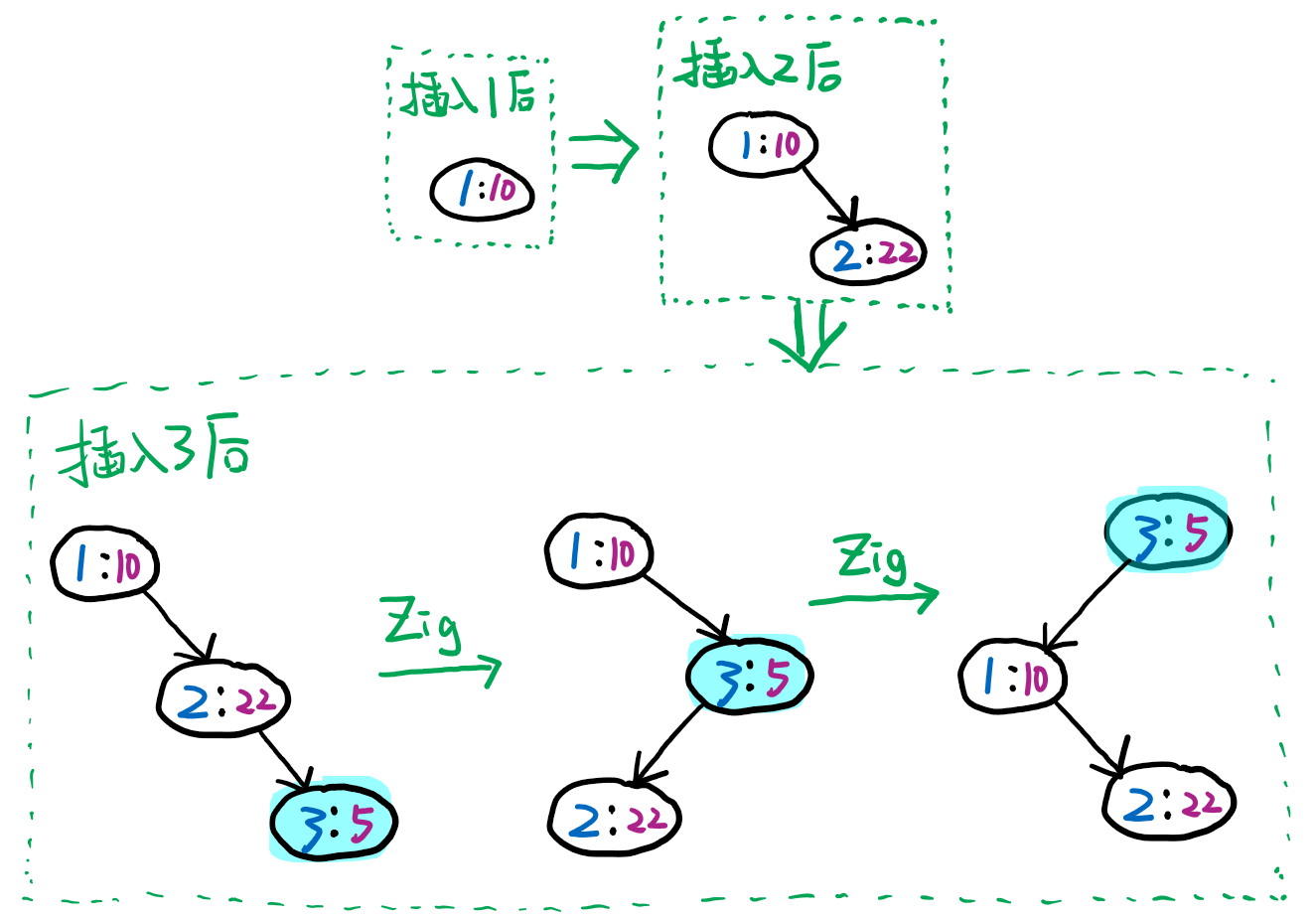
插入 \(4\) 不需要进行旋转。
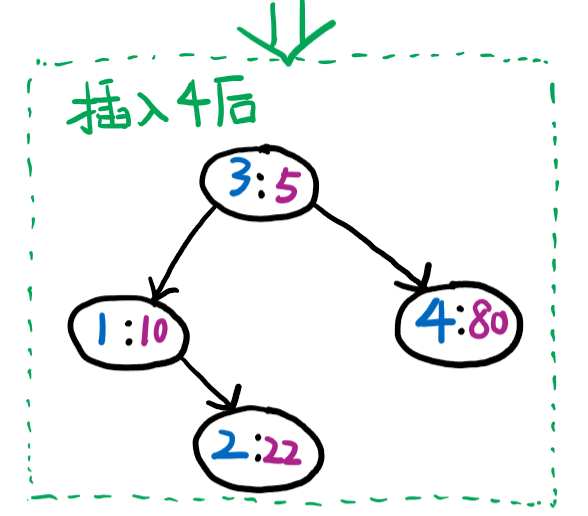
插入 \(5\) 之后要进行一次左旋。
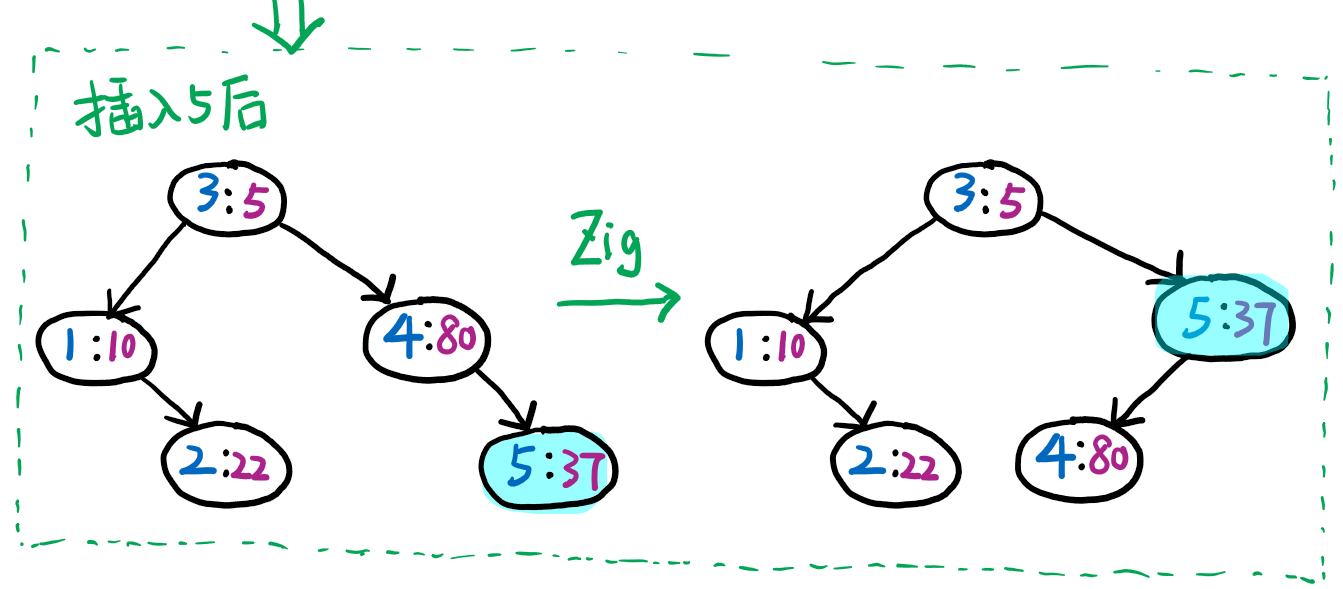
插入 \(6\) 之后不需要进行旋转。
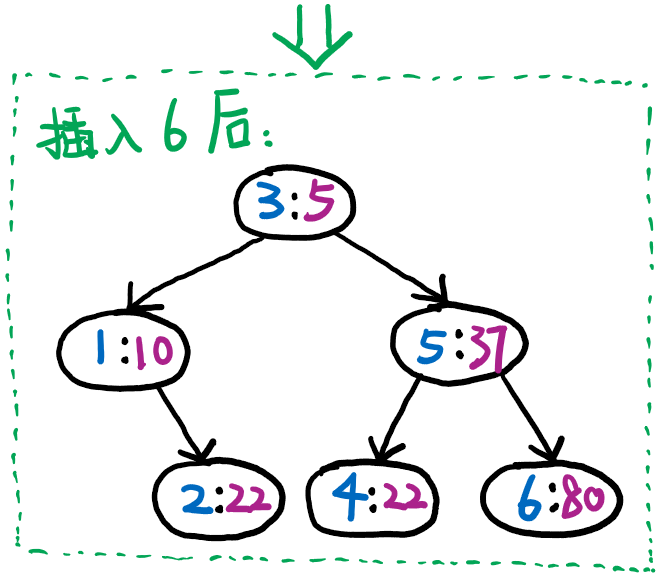
然后就完成了整棵树的插入。
通过观察,不难发现,如果把每个元素按照优先级大小的顺序(在上例中,即按照 \(3,1,2,5,4,6\) 的顺序)一次插入二叉排序树,形成的树和以上插入调整后的结果完全一致。这就是 Treap 的作用,使得数据插入实现了无关于数据本身的随机性,其效果与把数据打乱后插入完全相同,这使得它几乎能应用于所有需要使用平衡树的地方。
如果把插入的过程写成递归形式,只要在递归调用完成后判断是否满足堆的性质,如果不满足就继续旋转,实现起来也非常容易。由于旋转操作的时间复杂度是 \(O(1)\),最多只要进行 \(h\) 次旋转(\(h\) 是树的高度),所以总的时间复杂度为 \(O(h)\)。
3. 删除
有了旋转操作之后,Treap的删除比二叉排序树还要简单。因为Treap满足堆性质,所以我们只需要把要删除的节点旋转成叶节点,然后直接删除就可以了。具体的做法就是每次找到优先级小的孩子,向与其相反方向旋转,直到那个节点被旋转成了叶节点,然后直接删除即可。
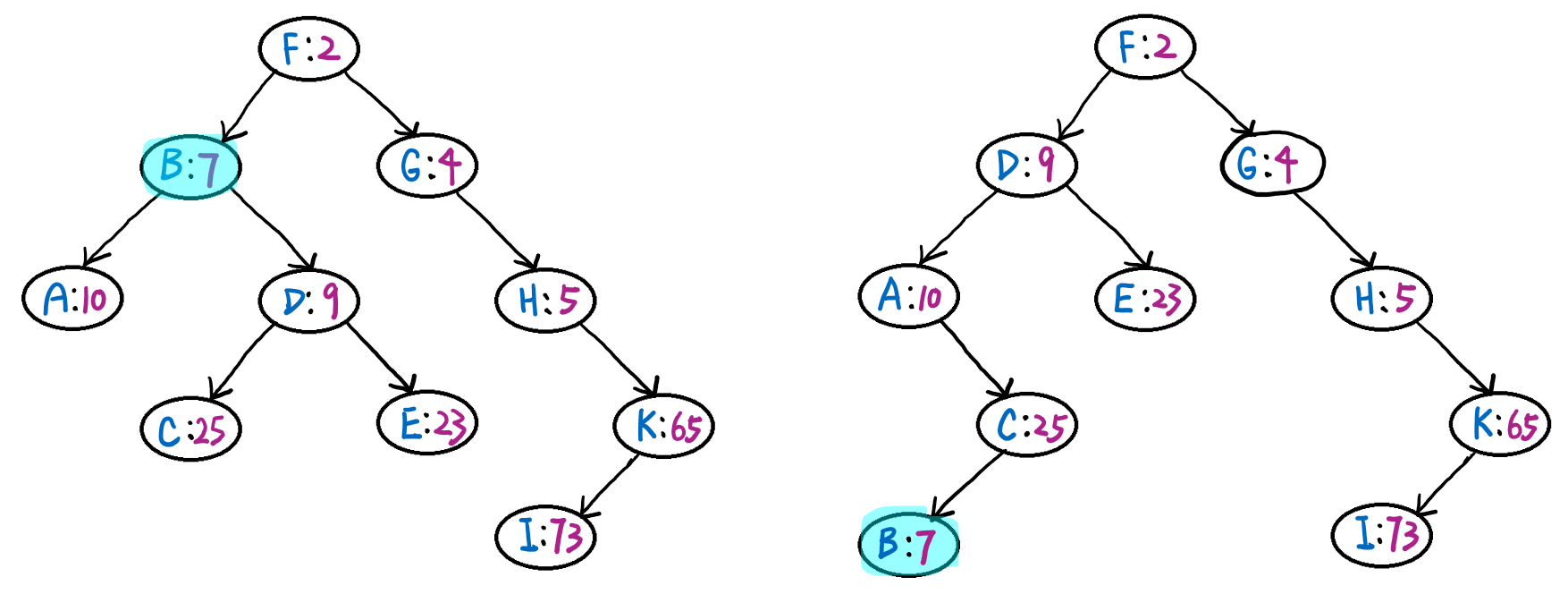
例如,要删除下图(左图)中的节点 \((B:7)\),旋转的结果如下图(右图)所示,再删除节点 \((B:7)\)。删除最多进行 \(h\) 次旋转,所以删除的时间复杂度是 \(O(h)\)。
4. 分离
要把一个Treap按大小分成两个Treap,只需要在分开的位置强行增加一个虚拟节点(设好优先级),然后依据优先级旋转至根节点再将其删除掉,左右两棵子树就是两个Treap了。根据二叉排序树的性质,这时左子树的所有节点都小于右子树的节点。分离的时间复杂度相当于一次插入操作的时间复杂度,也是 \(O(h)\)。
5. 合并
合并是指把两棵平衡树合并成一棵平衡树,其中第一棵树的所有节点都必须小于或等于第二棵树中的所有节点,这也是上面的分离操作的结果所满足的条件。Treap合并操作的过程和分离过程相反,只要曾姐一个虚拟的根,把两棵树分别作为左右子树,然后再把根删除就可以了。合并的时间复杂度和删除一样,也是 \(O(h)\)。
Treap的算法实现
首先定义一些需要的数据,即声明好结构体的功能:
int val[maxn], // 关键字
priority[maxn], // 优先级
lson[maxn], // 左二子编号
rson[maxn], // 右儿子编号
p[maxn], // 父节点编号
sz; // 元素个数
struct Treap {
int rt; // 根节点编号
void zig(int x); // 左旋
void zag(int x); // 右旋
void func_rotate(int x); // 旋转(左旋+右旋)
void add(int v); // 插入一个值v
int func_find(int v); // 查找值为v的元素
void del(int v); // 删除一个值为v的元素
int getMin(); // 获得最小值
int getMax(); // 获得最大值
int getPre(int v); // 获得前趋(值<=v的最大元素)
int getSuc(int v); // 获得后继(值>=v的最小元素)
} tree;
然后定义左旋和右旋的功能:
// 左旋
void Treap::zig(int x) {
int y = p[x], z = p[y];
assert(y && rson[y] == x);
if (rt == y) rt = x; // 更新rt
int b = lson[x];
rson[y] = b;
p[b] = y;
lson[x] = y;
p[y] = x;
p[x] = z;
if (z) {
if (lson[z] == y) lson[z] = x;
else rson[z] = x;
}
}
// 右旋
void Treap::zag(int x) {
int y = p[x], z = p[y];
assert(y && lson[y] == x);
if (rt == y) rt = x; // 更新rt
int b = rson[x];
lson[y] = b;
p[b] = y;
rson[x] = y;
p[y] = x;
p[x] = z;
if (z) {
if (lson[z] == y) lson[z] = x;
else rson[z] = x;
}
}
左旋与右旋的实现需要注意以下几个问题:
- 针对子节点 \(x\) 或者父节点 \(y\) 都可以(我的实现中都是针对子节点 \(x\) 的);
- 旋转的前提是: \(x\) 必须得有父节点,也就是说不能把根节点通过旋转向上调;
- 要注意有些子树可能是不存在的,不存在的节点定义成 \(0\) 即可;
- 如果节点有父节点,子节点指向新的父节点后,原先的父节点的子节点信息也得改变,父子关系的调整是双向的 —— 我不是你的儿子了,那么同时你也不是我的父亲了。
由于左旋和右旋的目的都是为了将子节点 \(x\) 向上调整一层,所以我们可以封装好一个 func_rotate 函数用于统一左旋和右旋操作:
// 旋转(左旋+右旋)
void Treap::func_rotate(int x) {
assert(p[x]);
if (x == rson[p[x]]) zig(x);
else zag(x);
}
插入:
// 插入一个值v
void Treap::add(int v) {
val[++sz] = v;
priority[sz] = rand();
if (!rt) rt = sz;
else {
int x = rt;
while (true) {
if (val[x] >= v) {
if (lson[x]) x = lson[x];
else {
lson[x] = sz;
p[sz] = x;
break;
}
}
else {
if (rson[x]) x = rson[x];
else {
rson[x] = sz;
p[sz] = x;
break;
}
}
}
x = sz;
while (p[x] && priority[x] < priority[p[x]]) func_rotate(x);
}
}
查询:
// 查找值为v的元素
int Treap::func_find(int v) {
if (!rt) return 0;
int x = rt;
while (true) {
if (val[x] == v) return x;
else if (val[x] > v) {
if (lson[x]) x = lson[x];
else return 0;
}
else { // val[x] < v
if (rson[x]) x = rson[x];
else return 0;
}
}
}
删除:
// 删除一个值为v的元素
void Treap::del(int v) {
int x = func_find(v);
if (!x) return;
while (lson[x] || rson[x]) {
if (!rson[x]) func_rotate(lson[x]);
else if (!lson[x]) func_rotate(rson[x]);
else if (priority[lson[x]] < priority[rson[x]]) func_rotate(lson[x]);
else func_rotate(rson[x]);
}
// 循环退出时x变成了叶子节点,删除它
if (x == rt) { // 叶子节点==根节点 --> 就1个节点
rt = 0;
return;
}
int y = p[x];
if (y) {
if (lson[y] == x) lson[y] = 0;
else rson[y] = 0;
}
p[x] = 0; // 这句不写也没关系
}
求最小值:
// 获得最小值
int Treap::getMin() {
int x = rt;
while (lson[x]) x = lson[x];
return x;
}
求最大值:
// 获得最大值
int Treap::getMax() {
int x = rt;
while (rson[x]) x = rson[x];
return x;
}
求前趋:
// 获得前趋(值<=v的最大元素)
int Treap::getPre(int v) {
if (!rt) return 0;
int ans = 0, x = rt;
while (x) {
if (val[x] <= v) {
if (ans == 0 || val[ans] < val[x]) ans = x;
x = rson[x];
}
else x = lson[x];
}
return ans;
}
求后继:
// 获得后继(值>=v的最小元素)
int Treap::getSuc(int v) {
if (!rt) return 0;
int ans = 0, x = rt;
while (x) {
if (val[x] >= v) {
if (ans == 0 || val[ans] > val[x]) ans = x;
x = lson[x];
}
else x = rson[x];
}
return ans;
}
完整的代码如下(对应《怪物仓库管理员(二)》):
#include <bits/stdc++.h>
using namespace std;
const int maxn = 1000010;
int val[maxn], // 关键字
priority[maxn], // 优先级
lson[maxn], // 左二子编号
rson[maxn], // 右儿子编号
p[maxn], // 父节点编号
sz; // 元素个数
struct Treap {
int rt; // 根节点编号
void zig(int x); // 左旋
void zag(int x); // 右旋
void func_rotate(int x); // 旋转(左旋+右旋)
void add(int v); // 插入一个值v
int func_find(int v); // 查找值为v的元素
void del(int v); // 删除一个值为v的元素
int getMin(); // 获得最小值
int getMax(); // 获得最大值
int getPre(int v); // 获得前趋(值<=v的最大元素)
int getSuc(int v); // 获得后继(值>=v的最小元素)
} tree;
// 左旋
void Treap::zig(int x) {
int y = p[x], z = p[y];
assert(y && rson[y] == x);
if (rt == y) rt = x; // 更新rt
int b = lson[x];
rson[y] = b;
p[b] = y;
lson[x] = y;
p[y] = x;
p[x] = z;
if (z) {
if (lson[z] == y) lson[z] = x;
else rson[z] = x;
}
}
// 右旋
void Treap::zag(int x) {
int y = p[x], z = p[y];
assert(y && lson[y] == x);
if (rt == y) rt = x; // 更新rt
int b = rson[x];
lson[y] = b;
p[b] = y;
rson[x] = y;
p[y] = x;
p[x] = z;
if (z) {
if (lson[z] == y) lson[z] = x;
else rson[z] = x;
}
}
// 旋转(左旋+右旋)
void Treap::func_rotate(int x) {
assert(p[x]);
if (x == rson[p[x]]) zig(x);
else zag(x);
}
// 插入一个值v
void Treap::add(int v) {
val[++sz] = v;
priority[sz] = rand();
if (!rt) rt = sz;
else {
int x = rt;
while (true) {
if (val[x] >= v) {
if (lson[x]) x = lson[x];
else {
lson[x] = sz;
p[sz] = x;
break;
}
}
else {
if (rson[x]) x = rson[x];
else {
rson[x] = sz;
p[sz] = x;
break;
}
}
}
x = sz;
while (p[x] && priority[x] < priority[p[x]]) func_rotate(x);
}
}
// 查找值为v的元素
int Treap::func_find(int v) {
if (!rt) return 0;
int x = rt;
while (true) {
if (val[x] == v) return x;
else if (val[x] > v) {
if (lson[x]) x = lson[x];
else return 0;
}
else { // val[x] < v
if (rson[x]) x = rson[x];
else return 0;
}
}
}
// 删除一个值为v的元素
void Treap::del(int v) {
int x = func_find(v);
if (!x) return;
while (lson[x] || rson[x]) {
if (!rson[x]) func_rotate(lson[x]);
else if (!lson[x]) func_rotate(rson[x]);
else if (priority[lson[x]] < priority[rson[x]]) func_rotate(lson[x]);
else func_rotate(rson[x]);
}
// 循环退出时x变成了叶子节点,删除它
if (x == rt) { // 叶子节点==根节点 --> 就1个节点
rt = 0;
return;
}
int y = p[x];
if (y) {
if (lson[y] == x) lson[y] = 0;
else rson[y] = 0;
}
p[x] = 0; // 这句不写也没关系
}
// 获得最小值
int Treap::getMin() {
int x = rt;
while (lson[x]) x = lson[x];
return x;
}
// 获得最大值
int Treap::getMax() {
int x = rt;
while (rson[x]) x = rson[x];
return x;
}
// 获得前趋(值<=v的最大元素)
int Treap::getPre(int v) {
if (!rt) return 0;
int ans = 0, x = rt;
while (x) {
if (val[x] <= v) {
if (ans == 0 || val[ans] < val[x]) ans = x;
x = rson[x];
}
else x = lson[x];
}
return ans;
}
// 获得后继(值>=v的最小元素)
int Treap::getSuc(int v) {
if (!rt) return 0;
int ans = 0, x = rt;
while (x) {
if (val[x] >= v) {
if (ans == 0 || val[ans] > val[x]) ans = x;
x = lson[x];
}
else x = rson[x];
}
return ans;
}
int n, op, x;
int main() {
scanf("%d", &n);
while (n --) {
scanf("%d", &op);
if (op != 3 && op != 4) scanf("%d", &x);
if (op == 1) tree.add(x);
else if (op == 2) tree.del(x);
else if (op == 3) printf("%d\n", val[tree.getMin()]);
else if (op == 4) printf("%d\n", val[tree.getMax()]);
else if (op == 5) printf("%d\n", val[tree.getPre(x)]);
else printf("%d\n", val[tree.getSuc(x)]);
}
return 0;
}

 浙公网安备 33010602011771号
浙公网安备 33010602011771号