洛谷P2239 螺旋矩阵 题解 模拟

题目链接：https://www.luogu.com.cn/problem/P2239

最暴力的解法就是从左上角开始遍历，一开始往右走，到头了右转往下走，到头了右转往左走，到头了右转往上走，……，一次循环。

此算法的时间复杂度为 \(O(n^2) = O(9 \times 10^8)\)，在洛谷是可以过的。

但是我们其实可以把矩阵看成一个个圈，可以发现：最外面的圈一共有 \(4 \times (n-1)\) 个数字，第 \(2\) 外面的圈一共有 \(4 \times (n-3)\) 个数字，……，第 \(i\) 圈一共有 \(4 \times (n-2 \cdot i + 1)\) 个数字……（如果 \(n\) 为奇数则最后那一圈就只有一个数字）。

而根据给我们的坐标 \((i,j)\) 我们可以快速确定这个点在第 \(k = min(min(i,n-i+1), min(j,n-j+1))\) 圈，而第 \(1\) 圈到第 \(k-1\) 圈的数字总共有

\[\sum_{i=1}^{k-1} 4 \times (n - 2 \cdot i + 1) = 4 \cdot (n + 1 - k) \cdot (k-1) \]

而第 \(k\) 圈的起始位置为 \((k,k)\) ，我们从这里开始判断即可。

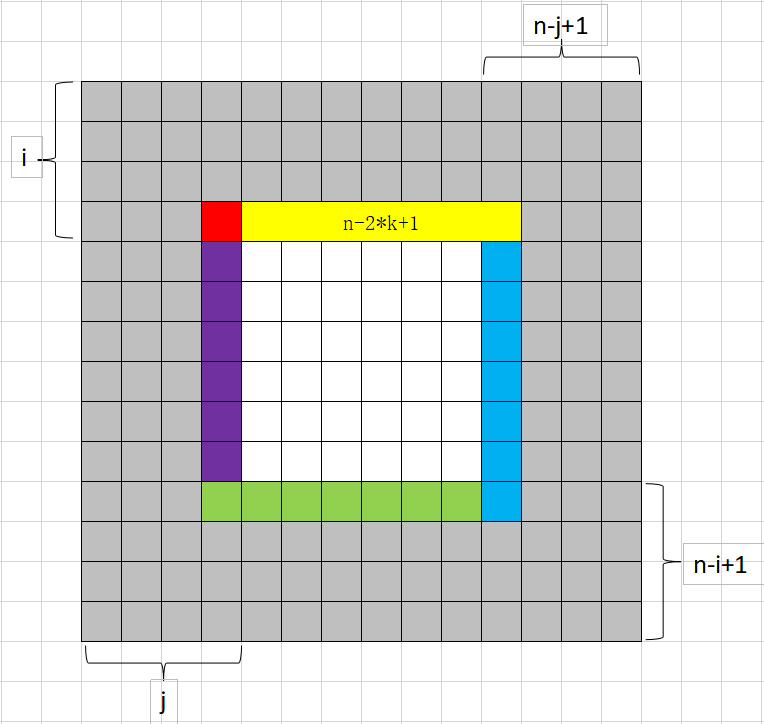
• 如果 \(i = k\)，则 \((i,j)\) 编号为 \(4 \cdot (n + 1 - k) \cdot (k-1) + 1 + j - k\)；
• 否则，如果 \(j = n+1-k\)，则 \((i,j)\) 编号为 \(4 \cdot (n + 1 - k) \cdot (k-1) + 1 + (n-2 \cdot k+1) + i-k\)；
• 否则，如果 \(i = n+1-k\)，则 \((i,j)\) 编号为 \(4 \cdot (n + 1 - k) \cdot (k-1) + 1 + 2 \cdot (n-2 \cdot k+1) + (n+1-k)-j\)；
• 否则，如果 \(j = k\)，则 \((i,j)\) 编号为 \(4 \cdot (n + 1 - k) \cdot (k-1) + 1 + 3 \cdot (n-2 \cdot k+1) + (n+1-k) - i\)。

实现代码如下：

#include <bits/stdc++.h>
using namespace std;
int n, i, j, k, ans;
int main() {
    cin >> n >> i >> j;
    k = min( min(i, n+1-i), min(j, n+1-j) );
    ans = 4 * (n+1-k) * (k-1) + 1;
    if (i == k) ans += j-k;
    else if (j == n+1-k) ans += (n-2*k+1) + i-k;
    else if (i == n+1-k) ans += 2*(n-2*k+1) + (n+1-k)-j;
    else ans += 3*(n-2*k+1) + (n+1-k)-i;
    cout << ans << endl;
    return 0;
}