Codeforces Round #604 (Div. 2) E. Beautiful Mirrors 题解 组合数学

题目链接：https://codeforces.com/contest/1265/problem/E

题目大意：
有 \(n\) 个步骤，第 \(i\) 个步骤成功的概率是 \(P_i\) ，每一步只有成功了才会进入下一步，失败了会从第 \(1\) 步重新开始测。请问成功的期望步数是多少？

解题思路：
设期望步数是 \(S\) ，则有公式如下：

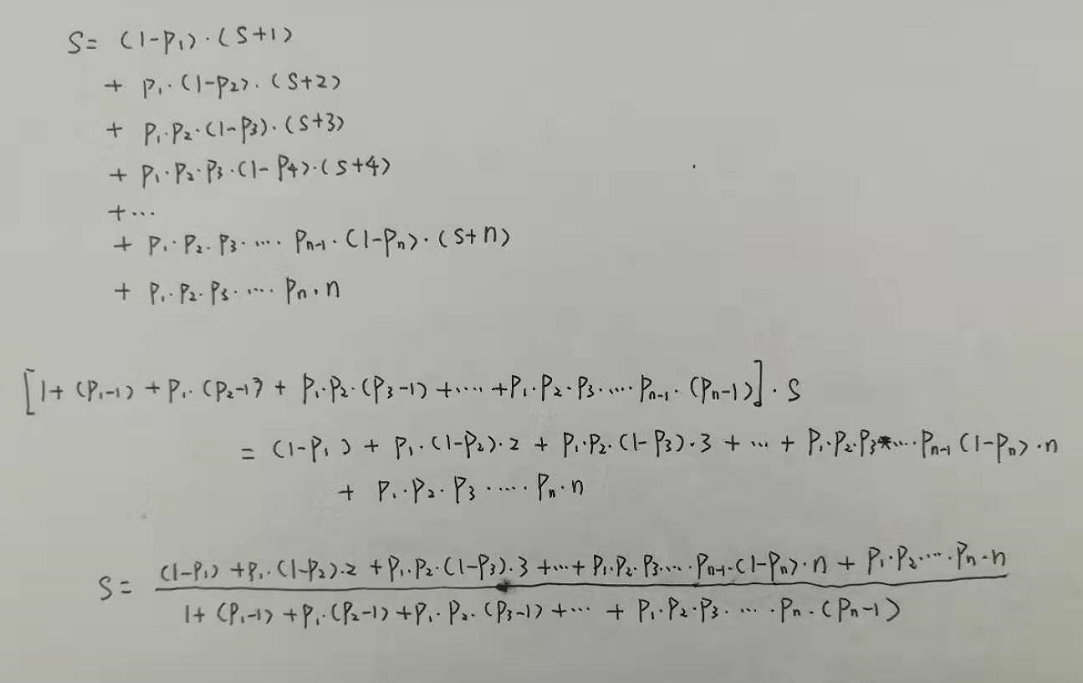
实现代码如下：

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int maxn = 200020;
const ll MOD = 998244353LL;
 
void gcd(ll a , ll b , ll &d , ll &x , ll &y) {
    if(!b) {d = a; x = 1; y = 0;}
    else { gcd(b , a%b,d,y , x); y -= x * (a/b); }
}
ll inv(ll a , ll n) {
    ll d , x , y;
    gcd(a , n , d,  x , y);
    return d == 1 ? (x+n)%n : -1;
}
 
int n;
ll a[maxn], p[maxn], s[maxn];
int main() {
    scanf("%d", &n);
    for (int i = 1; i <= n; i ++) scanf("%lld", &a[i]);
    for (int i = 1; i <= n; i ++) {
        p[i] = a[i] * inv(100, MOD) % MOD;
    }
    s[0] = 1;
    for (int i = 1; i <= n; i ++) s[i] = s[i-1] * p[i] % MOD;
    ll x = 0, y = 0;
    for (int i = 1; i <= n; i ++) {
        x = (x + s[i-1] * (1 - p[i] + MOD) % MOD) % MOD;
        y = (y + s[i-1] * (1 - p[i] + MOD) % MOD * i % MOD) % MOD;
    }
    y = (y + s[n] * n % MOD) % MOD;
    x = (1 - x + MOD) % MOD;
    ll res = y * inv(x, MOD) % MOD;
    printf("%lld\n", res);
    return 0;
}