洛谷P1720 月落乌啼算钱 题解 斐波那契数列/特征方程求解

题目链接：https://www.luogu.com.cn/problem/P1720
题目描述：
给你一个公式 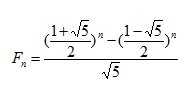，求对应的 \(F_n\) 。
解题思路：
首先不难想象这是一个斐波那契数列，我们可以通过找规律等方式来求解得到答案。
但是这里想说一下的还是这个公式的推导过程。
斐波那契数列的数学公式是通过 数列特征方程 来进行求解的。
首先，对于斐波那契数列，我们知道 \(f_{n+2} = f_{n+1} + f_{n}\)
我们不妨设等比数列的公比为 \(q\) ，则

\[q^2 \times f_n = q \times f_n + f_n \]

约去 \(f_n\) 得：

\[q^2 - q - 1 = 0 \]

得：\(q_1 = \frac{1 + \sqrt{5}}{2},q_2 = \frac{1 - \sqrt{5}}{2}\)

所以 \(f_n\) 是 \(q_1^n\) 和 \(q_2^n\) 的一个线性组合，
我们假设 \(f_n = A \times q_1^n + B \times q_2^n\) ，带入 \(f_1 = f_2 = 1\) ，得：

\[f_n = \frac{\sqrt{5}}{5}(\frac{1 + \sqrt{5}}{2})^{n} - \frac{\sqrt{5}}{5}(\frac{1 - \sqrt{5}}{2})^{n} \]

在了解这个思想之后，我们还是按照递推公式计算斐波那契数列数列比较方便。

实现代码如下：

#include <bits/stdc++.h>
using namespace std;
long long f[50];
int n;
int main() {
    cin >> n;
    f[1] = f[2] = 1;
    for (int i = 3; i <= n; i ++) f[i] = f[i-1] + f[i-2];
    cout << f[n] << ".00" << endl;
    return 0;
}