据说最近IMO中国队失利的一题
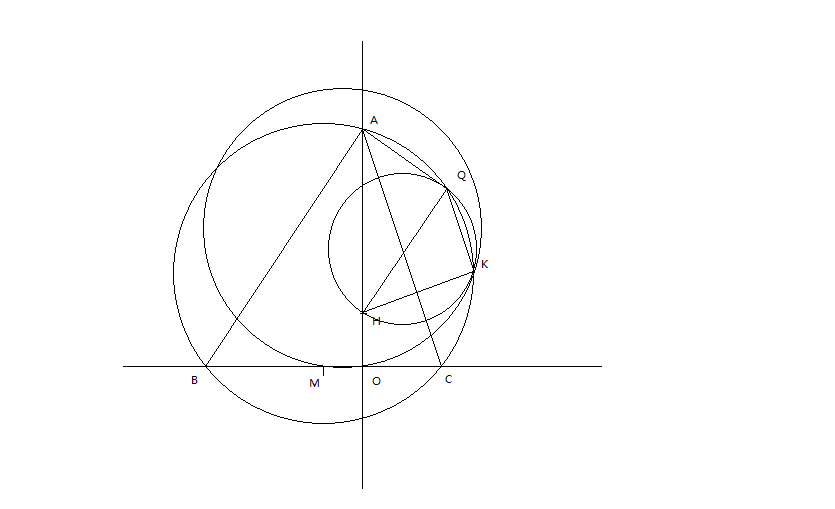
(图基于Microsoft PaintBrush技术构建)
平面几何是可以难得出蛆的。这道题难在多圆、高度非对称和具有一定复杂性。如图,对ABC,H是垂心,O是垂足,M是中点。QK在ABC外接圆上,均在图中小三角形上构成直角。现需要证明:三角形QHK的外接圆和MOK的的外接圆相切。
如果解析,估计也就做如图的坐标了,到求Q的坐标就可能需要解二元二次方程,K更不知道了。然后,没有然后了。
硬上,然后下去:
容易的点的坐标:
A(0,a)
B (-b,0)
C (c,0)
M ((c-b)/2, 0)
H (0, bc/a)
大圆圆心:( (c-b)/2, (a^2-bc)/2a ),半径:sqrt((a^2+b^2)*(a^2+c^2))/2a
三角形AQH的外接圆圆心:( 0, (a^2+bc)/2a),半径:(a^2-bc)/2a
接下来是关键部分,解析分析上部的直角三角形组,从而求出Q和K的坐标。
可以发现用解析法,会出现多项式爆炸,奈么完结。
于是只有用上述解析中发现的一条平面几何定理(外接圆圆心到边的距离为垂心到对顶点的距离的一半)为突破口,发现这些点之间关联存在以下框架(这个框架非常似曾相识,也许以前看到过或者类似低阶题目):
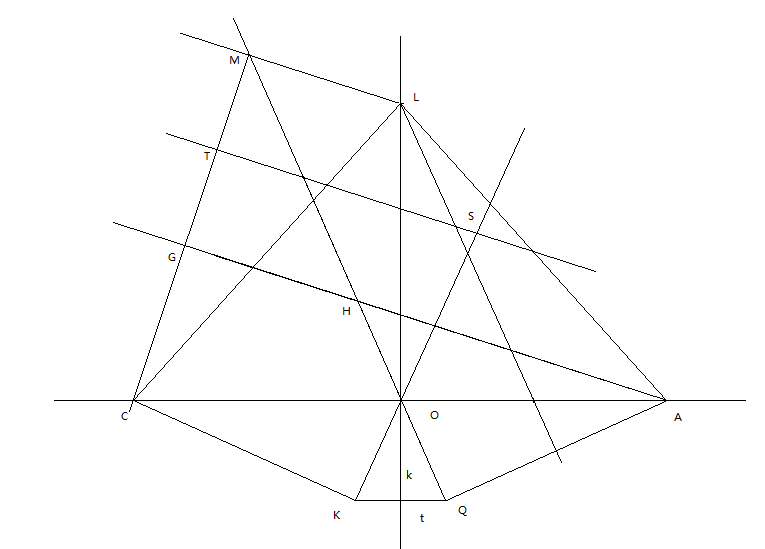
这其中L为原来三角形ABC的外接圆圆心,G为原图中垂足O,T为MG的中点。显然LKQ、OKQ、LCK、LQA为等腰三角形,形成关于y轴镜面对称结构,O处为原点可建立显然如图的直角坐标系。角OQA,OKC为直角,所以MQ和L向QA作的垂线平行。H和K关于x轴镜面对称。设Q的坐标为(-t, k)(于是显然K为(-t, -k),H为(-t, k)),根据显然的相似关系A的坐标为(a, 0) = (k^2+t^2/t, 0),L的坐标为(0, ka/2t)。
HA的方程易求,HA和y轴的交点坐标为ak/(a+t)。由上述关系,显然TS和y轴的交点为L和HA与y轴交点的中点,即:(k a^2 + 3a k t) / 4 t (a + t)。
LM和AH平行,AH被L对QA垂线平分,显然平分点和HML构成平行四边形,于是容易求出M的坐标为(-(a+t)/2, ka/2t+k/2)。
进一步,TS与GA平行,所以斜率也是-k/(a+t),于是由TS的方程和OS的方程,得到S的坐标为( (a^2+3 a t) / 4(a+2t), k(a^2+3 a t) / 4 t (a+2t) )。
于是最终只要证明,SM = SK。(根据以上算式可证,用数值已经验证几组无误;但wolfram居然不给力,不能正确解出,可能要用自制程序来展开验证)


