XJOI NOIP模拟题1
第一题
分析:
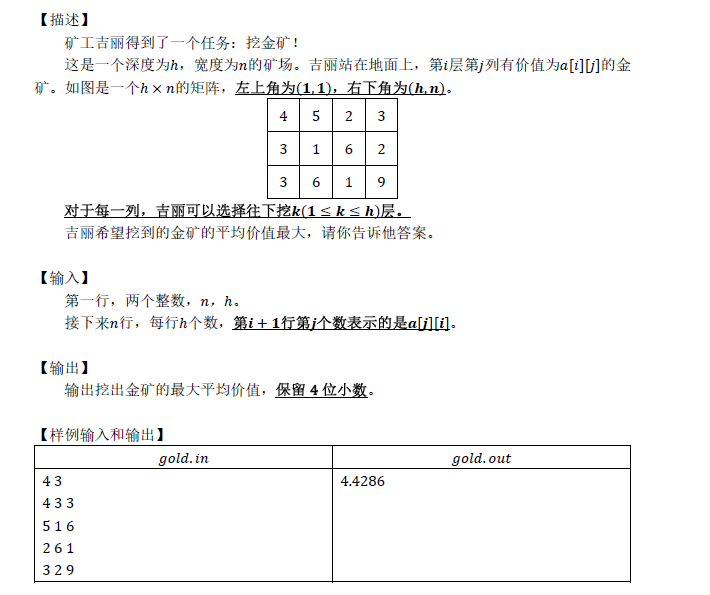
开始想的是贪心,取每列均值最大一段。
应该是01分数规划,具体看代码
代码:

program gold; var a:array[0..100000]of int64; n,i,m,j,x:longint; function max(x,y:real):real; begin if x>y then max:=x else max:=y; end; function cheak(x:real):boolean; var i,j:longint; s,ans:real; begin ans:=0; for i:=1 to n do begin s:=-1000000000; for j:=1 to m do begin s:=max(a[(i-1)*m+j]-j*x,s); end; ans:=ans+s; end; if ans>=0 then exit(true) else exit(false); end; procedure work; var l,r,mid:real; begin l:=0; r:=1000000000; while l+0.00001<=r do begin mid:=(l+r)/2; if cheak(mid) then l:=mid else r:=mid; end; writeln(l:0:4); end; begin readln(n,m); for i:=1 to n do begin for j:=1 to m do begin read(x); if j=1 then a[(i-1)*m+j]:=x else a[(i-1)*m+j]:=a[(i-1)*m+j-1]+x; end; end; work; end.
第二题

n最大10^5
分析:
第一反应是用图做,对相交城市连边再求最大团,这样显然是不够的。
稍经思考可以发现,这题跟火柴排队似乎有某种联系。
显然如果在上边一组中x在y左边,在下面一组城市x在y右边,两者必然相交。
如果底下一组是1 2 3 4 5有序的话,对于上面一组,如果x<y 而 x在y后面,则必有交点,实际上这就转化为了最长下降子序列问题,不过之前先要对上面一组对底下一组的排列进行映射。
代码:

program road; var d,a,b,w:array[0..100000]of longint; n,i,m,len,j,k:longint; function find(x:longint):longint; var l,r,mid,ans:longint; begin l:=1; r:=len; ans:=0; while l<=r do begin mid:=(l+r) div 2; if d[mid]<=x then begin ans:=mid; l:=mid+1; end else r:=mid-1; end; exit(ans); end; begin readln(n); for i:=1 to n do read(a[i]); for i:=1 to n do begin read(b[i]); w[b[i]]:=i; end; for i:=1 to n do a[i]:=w[a[i]]; d[1]:=a[n]; len:=1; for i:=n-1 downto 1 do begin if a[i]>d[len] then begin inc(len); d[len]:=a[i]; end else begin j:=find(a[i]); k:=j+1; d[k]:=a[i]; end; end; writeln(len); end.
第三题:

n,t最大10^5
分析:
先按编号顺序后根遍历树,得到一个序列,这个序列就是向里面逐个进人依次占用的结点。
对于op=1操作用堆维护
对于op=2操作,用倍增找祖先,找到最远的被占用的祖先,将该点的人带走(实际上是带走x点人的等效),并加入堆。
为什么时间效率可以过呢
不考虑op=2只会加n个人故为nlog2(n),增加op=2操作,因为每次只走1个人,最多走t人,则最多重新来t个人,这时op=1情况时间效率增加t*log2(n)
op=2本身还要有t*log2(n)的时间,故总时间效率为O(n*log2(n))。
代码:

program queue; type point=^node; node=record x:longint; next:point; end; var f:array[0..25,0..100000]of longint; q,d,a,b,g:array[0..100000]of longint; r:array[0..200000]of longint; w:array[0..100000]of point; n,i,m,t,e,k:longint; procedure use(x:longint); var t,s,v:longint; begin k:=k+1; r[k]:=x; s:=k; while (s<>1)and(r[s div 2]>r[s]) do begin v:=r[s div 2]; r[s div 2]:=r[s]; r[s]:=v; s:=s div 2; end; end; function get:longint; var t,s,v:longint; begin get:=r[1]; r[1]:=r[k]; k:=k-1; t:=1; while (t*2<=k)or(t*2+1<=k) do begin if (t*2+1>k)or(r[t*2]<r[t*2+1]) then s:=t*2 else s:=t*2+1; if r[t]>r[s] then begin v:=r[t]; r[t]:=r[s]; r[s]:=v; t:=s; end else break; end; end; procedure make; var i,j:longint; begin for i:=0 to 24 do for j:=1 to n do f[i+1,j]:=f[i,f[i,j]]; end; procedure dfs(x,fa:longint); var p:point;y:longint; begin new(p); p:=w[x]; f[0,x]:=fa; while p<>nil do begin y:=p^.x; if y<>fa then dfs(y,x); p:=p^.next; end; inc(m); q[m]:=x; end; procedure add(x,y:longint); var p:point; begin new(p); p^.x:=y; p^.next:=w[x]; w[x]:=p; end; procedure insert(x:longint); var i,y:longint; begin for i:=1 to x do begin y:=get; d[y]:=1; end; writeln(q[y]); end; procedure put(x:longint); var i,s:longint; begin s:=0; for i:=25 downto 0 do if (d[g[f[i,x]]]=1)and(f[i,x]>0) then begin x:=f[i,x]; s:=s+1 shl i; end; d[g[x]]:=0; use(g[x]); writeln(s); end; procedure solve; var i,op,x:longint; begin for i:=1 to t do begin readln(op,x); if op=1 then begin insert(x); end else begin put(x); end; end; end; procedure qsort(l,h:longint); var i,j,t,m,m1:longint; begin i:=l; j:=h; m:=a[(i+j) div 2]; m1:=b[(i+j) div 2]; repeat while (a[i]<m)or((a[i]=m)and(b[i]>m1)) do inc(i); while (m<a[j])or((a[j]=m)and(m1>b[j])) do dec(j); if i<=j then begin t:=a[i]; a[i]:=a[j]; a[j]:=t; t:=b[i]; b[i]:=b[j]; b[j]:=t; inc(i); dec(j); end; until i>j; if i<h then qsort(i,h); if j>l then qsort(l,j); end; begin readln(n,t); for i:=1 to n-1 do readln(a[i],b[i]); qsort(1,n-1); m:=0; for i:=1 to n-1 do add(a[i],b[i]); for i:=1 to n-1 do begin e:=a[i]; a[i]:=b[i];b[i]:=e; end; qsort(1,n-1); for i:=1 to n-1 do add(a[i],b[i]); dfs(1,0); k:=0; for i:=1 to n do g[q[i]]:=i; for i:=1 to n do begin use(i); d[i]:=0; end; make; solve; end.




