bzoj 3218: a + b Problem

Description

 

Input

Output

Sample Input

Sample Output

HINT

Source 

传说中的可持久化线段树优化网络流。。。

做了一些预备题后最小割建图还是比较简单，但边数是n^2。

每次可以通过向值域中的区间连边，使边数降为nlogn，要满足j<i，打一个可持久化，每次搞完再insert即可

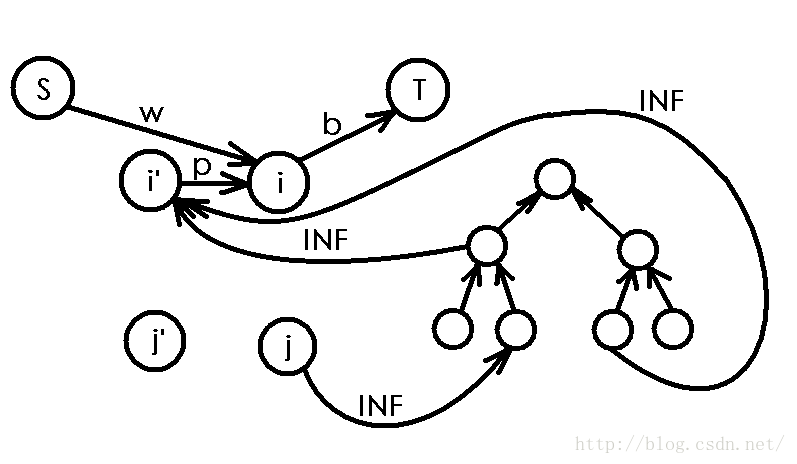
蒯一个PoPoQQQ大爷的图，很清楚啊。。。

 

// MADE BY QT666
#include<cstdio>
#include<algorithm>
#include<cmath>
#include<iostream>
#include<cstring>
#define RG register
using namespace std;
typedef long long ll;
const int N=1000050;
const int Inf=19260817;
int gi(){
  int x=0,flag=1;
  char ch=getchar();
  while(ch<'0'||ch>'9'){if(ch=='-') flag=-1;ch=getchar();}
  while(ch>='0'&&ch<='9') x=x*10+ch-'0',ch=getchar();
  return x*flag;
}
int head[N],nxt[N],to[N],s[N],cnt=1,level[N],q[N],S,T,F;
int a[5050],b[5050],w[5050],l[5050],r[5050],p[5050],n,tot;
int sz,ls[100050],rs[100050],root[100050],hsh[100050],sum,goal,hh=0;
inline void Addedge(RG int x,RG int y,RG int z) {
  to[++cnt]=y,s[cnt]=z,nxt[cnt]=head[x],head[x]=cnt;
}
inline void lnk(RG int x,RG int y,RG int z){
  if(!x||!y) return;
  Addedge(x,y,z),Addedge(y,x,0);
}
inline bool bfs(){
  for(RG int i=1;i<=sz;i++) level[i]=0;
  q[0]=S,level[S]=1;int t=0,sum=1;
  while(t<sum){
    int x=q[t++];
    if(x==T) return 1;
    for(RG int i=head[x];i;i=nxt[i]){
      int y=to[i];
      if(s[i]&&level[y]==0){
	level[y]=level[x]+1;
	q[sum++]=y;
      }
    }
  }
  return 0;
}
inline int dfs(RG int x,int maxf){
  if(x==T) return maxf;
  int ret=0;
  for(RG int i=head[x];i;i=nxt[i]){
    int y=to[i],f=s[i];
    if(level[y]==level[x]+1&&f){
      int minn=min(f,maxf-ret);
      f=dfs(y,minn);
      s[i]-=f,s[i^1]+=f,ret+=f;
      if(ret==maxf) break;
    }
  }
  if(!ret) level[x]=0;
  return ret;
}
inline void Dinic(){
  while(bfs()) F+=dfs(S,Inf);
}
inline void insert(int l,int r,int x,int &y,int v){
  y=++sz;ls[y]=ls[x],rs[y]=rs[x];hh++;
    lnk(x,y,Inf);lnk(goal,y,Inf);
    if(l==r) return;
    int mid=(l+r)>>1;
    if(v<=mid) insert(l,mid,ls[x],ls[y],v);
    else insert(mid+1,r,rs[x],rs[y],v);
}
inline void query(int x,int L,int R,int xl,int xr){
  if(!x) return;
  if(xl<=L&&R<=xr){lnk(x,goal,Inf);return;}
  int mid=(L+R)>>1;
  if(xl<=mid) query(ls[x],L,mid,xl,xr);
  if(xr>mid) query(rs[x],mid+1,R,xl,xr);
}
int main(){
  n=gi();S=2*n+1;T=2*n+2;sz=T;
  for(RG int i=1;i<=n;i++){
    a[i]=gi(),b[i]=gi(),w[i]=gi(),l[i]=gi(),r[i]=gi(),p[i]=gi();
    tot+=b[i],tot+=w[i];hsh[++sum]=a[i];
  }
  sort(hsh+1,hsh+1+sum);sum=unique(hsh+1,hsh+sum+1)-hsh-1;
  for(int i=1;i<=n;i++){
    a[i]=lower_bound(hsh+1,hsh+1+sum,a[i])-hsh;
    l[i]=lower_bound(hsh+1,hsh+1+sum,l[i])-hsh;
    r[i]=upper_bound(hsh+1,hsh+1+sum,r[i])-hsh-1;
    lnk(S,i,w[i]);lnk(i,T,b[i]);lnk(i+n,i,p[i]);
  }
  for(int i=1;i<=n;i++){
    goal=i+n;if(l[i]<=r[i]) query(root[i-1],1,sum,l[i],r[i]);
    goal=i;insert(1,sum,root[i-1],root[i],a[i]);
  }
  Dinic();printf("%d\n",tot-F);
  return 0;
}