bzoj 1597: [Usaco2008 Mar]土地购买
Description
农 夫John准备扩大他的农场,他正在考虑N (1 <= N <= 50,000) 块长方形的土地. 每块土地的长宽满足(1 <= 宽 <= 1,000,000; 1 <= 长 <= 1,000,000). 每块土地的价格是它的面积,但FJ可以同时购买多快土地. 这些土地的价格是它们最大的长乘以它们最大的宽, 但是土地的长宽不能交换. 如果FJ买一块3x5的地和一块5x3的地,则他需要付5x5=25. FJ希望买下所有的土地,但是他发现分组来买这些土地可以节省经费. 他需要你帮助他找到最小的经费.
Input
* 第1行: 一个数: N
* 第2..N+1行: 第i+1行包含两个数,分别为第i块土地的长和宽
Output
* 第一行: 最小的可行费用.
Sample Input
100 1
15 15
20 5
1 100
输入解释:
共有4块土地.
Sample Output
HINT
FJ分3组买这些土地: 第一组:100x1, 第二组1x100, 第三组20x5 和 15x15 plot. 每组的价格分别为100,100,300, 总共500.
Source
首先这个题仍然是一个划分性DP。。。
所以设的状态仍然和之前的划分性DP相同。。。
首先考虑最裸的暴力。。。
f[i]=min(f[j]+max(q[j+1到i].b)*max(q[j+1到i].a));
然后我们发现一个很严肃的问题。。。
这个方程在转移的时候有max那么显然是不会满足决策单调性的。。。
这个暴力可以通过ST表预处理实现n^2。然而这个复杂度是明显不行的。。。
我们要做的就是尽量的去掉这些max。。。去掉max的方法就是使这些权值都是单调的,那么我们直接查询端点即可,就不需要max了。。
首先考虑让a单调,这样通过一遍sort即可以做到。。。
然后方程变为了:
f[i]=min(f[j]+max(q[j+1到i].b)*q[i].a);
然而还是有一个max的仍然没有单调性,复杂度仍然是n^2;
那么我们如何再把b变成单调的呢???因为只有这样才能去掉max。。
如果把土地尺寸用二维坐标表示时:
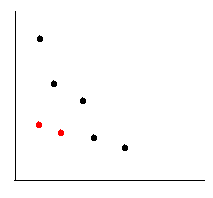
显然如果通过把a排序之后,图中两个红点是不会产生任何贡献的。。。
所以对于一个点在把a排了序之后,对于一个点如果后面还有b值大于他的b值时,这个点可以被覆盖掉(他不会有任何贡献)。。。
这个其实可以线性扫,然而我暴力打了ST表懒得删了
然后把这些点删掉之后,a权值是单调递增的,b权值是单调递减的。。。
方程被化为:
f[i]=min(f[j]+q[j+1].b*q[i].a);
这个式子就是一个经典的决策单调性式子了。。。
满足决策单调性,可以用二分栈完美解决了。。。nlogn
附上代码
// MADE BY QT666
#include<cstdio>
#include<algorithm>
#include<cmath>
#include<iostream>
#include<queue>
#include<set>
#include<cstdlib>
#include<cstring>
#include<string>
#include<ctime>
#define int long long
#define lson num<<1
#define rson num<<1|1
using namespace std;
typedef long long ll;
const int N=100050;
int gi()
{
int x=0,flag=1;
char ch=getchar();
while(ch<'0'||ch>'9'){if(ch=='-') flag=-1;ch=getchar();}
while(ch>='0'&&ch<='9') x=x*10+ch-'0',ch=getchar();
return x*flag;
}
struct ac{int a,b;}qq[N],nw[N];
struct data{int l,r,p;}q[N];
int n,f[N],pre[20],pre2[N],ST[N][20];
bool cmp(ac a,ac b){
return a.a<b.a;
}
int cal(int j,int i){
return f[j]+nw[j+1].b*nw[i].a;
}
void makeST()
{
pre[0]=1;for(int i=1;i<=18;i++) pre[i]=pre[i-1]<<1;
pre2[0]=-1;for(int i=1;i<=n;i++) pre2[i]=pre2[i>>1]+1;
for(int i=1;i<=n;i++) ST[i][0]=qq[i].b;
for(int j=1;j<=18;j++)
for(int i=1;i<=n;i++){
if(i+pre[j]-1<=n){
int x1=ST[i][j-1],x2=ST[i+pre[j-1]][j-1];
ST[i][j]=max(x1,x2);
}
}
}
int query(int l,int r)
{
if(l==r)return qq[l].b;
int x=pre2[r-l+1];
int x1=ST[l][x],x2=ST[r-pre[x]+1][x];
int ans=max(x1,x2);
return ans;
}
int find(data t,int x){
int l=t.l,r=t.r;
while(l<=r){
int mid=(l+r)>>1;
if(cal(t.p,mid)<cal(x,mid))
l=mid+1;
else r=mid-1;
}
return l;
}
main()
{
n=gi();
for(int i=1;i<=n;i++) qq[i].a=gi(),qq[i].b=gi();
sort(qq+1,qq+1+n,cmp);
makeST();
int tot=0;
for(int i=1;i<=n;i++){
if(qq[i].b>=query(i+1,n)){
nw[++tot]=qq[i];
}
}
int head=1,tail=0;
q[++tail]=(data){0,tot,0};
for(int i=1;i<=tot;i++){
while(head<=tail&&i>q[head].r) head++;
f[i]=cal(q[head].p,i);
if(head>tail||cal(i,tot)<=cal(q[tail].p,tot)){
while(head<=tail&&cal(i,q[tail].l)<=cal(q[tail].p,q[tail].l))
tail--;
if(head>tail)
q[++tail]=(data){i,tot,i};
else{
int t=find(q[tail],i);
q[tail].r=t-1;
q[++tail]=(data){t,tot,i};
}
}
}
printf("%lld",f[tot]);
}




