bzoj 3626: [LNOI2014]LCA
Description
给出一个n个节点的有根树(编号为0到n-1,根节点为0)。一个点的深度定义为这个节点到根的距离+1。
设dep[i]表示点i的深度,LCA(i,j)表示i与j的最近公共祖先。
有q次询问,每次询问给出l r z,求sigma_{l<=i<=r}dep[LCA(i,z)]。
(即,求在[l,r]区间内的每个节点i与z的最近公共祖先的深度之和)
Input
第一行2个整数n q。
接下来n-1行,分别表示点1到点n-1的父节点编号。
接下来q行,每行3个整数l r z。
Output
输出q行,每行表示一个询问的答案。每个答案对201314取模输出
Sample Input
0
0
1
1
1 4 3
1 4 2
Sample Output
5
HINT
共5组数据,n与q的规模分别为10000,20000,30000,40000,50000。
Source
Orz这题真的太鬼了,除了暴力求LCA再暴力求根本想不到该怎么做,小伙子啊,迟早要完!!!
看了题解之后膝盖又一次跪烂了。。。
于是接下来就一步一步还原大佬们是怎么YY出来的吧
新暴力雏形:
对于每个z,我们把z到根节点上的所有点都打上标记,然后对于区间[l,r]的点就不断向上跳爸爸,直到跳到一个打了标记的点,把这个点的深度加上。。。
也就是说只有这些被z跳到的点的深度才是有贡献的。。。
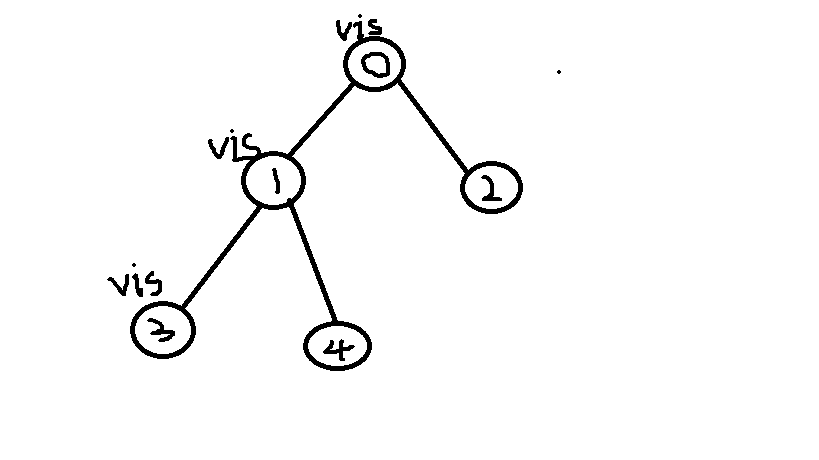
考虑到深度的定义。。。
于是有了并没有一点改进的暴力:
把z到根的路径上的点权加1,l--r中的每个点的贡献相当于查询该点到根节点的路径上的权值和(这个值也就等价于第一种暴力中找到的第一个有标记的点的深度。。。)

这样手动模拟或脑子YY是显然没有问题的。。。
我们发现这种操作是有可逆性的,重复性的(深度叠加)。。。
那么上面的第二种暴力的做法等价于如下做法:
把l--r间的每个点到根节点路径上的点权加1,然后对于每个z,其答案就是z到根的权值和。。。
于是就变成了下面这样:

于是我们可以想到一个比较明显的做法了。。。依次加入0--n-1的点并把该点到根的路径上的点权加1;
我们考虑用前缀和的思想,即用ans[r]-ans[l-1]。。。
我们对于每个询问的l和r拆成两个询问,把这些询问离线下来sort一遍,维护一个head指针一直加点。。。,head指针是单增的,
就不需要像CJK神犇那样对每个询问l和r还要打个莫队。。。
我们需要一个数据结构来维护区间修改和区间求和。。。于是我做死的打了一个LCT,相当于只要下放lazy和维护一个子树大小。。。
附上代码:
1 // MADE BY QT666 2 #include<cstdio> 3 #include<algorithm> 4 #include<cmath> 5 #include<iostream> 6 #include<queue> 7 #include<set> 8 #include<cstdlib> 9 #include<cstring> 10 #include<string> 11 #include<ctime> 12 #define lson num<<1 13 #define rson num<<1|1 14 #define int long long 15 using namespace std; 16 typedef long long ll; 17 const int N=100050; 18 const int mod=201314; 19 int gi() 20 { 21 int x=0,flag=1; 22 char ch=getchar(); 23 while(ch<'0'||ch>'9'){if(ch=='-') flag=-1;ch=getchar();} 24 while(ch>='0'&&ch<='9') x=x*10+ch-'0',ch=getchar(); 25 return x*flag; 26 } 27 int c[N][2],fa[N],st[N],sum[N],rev[N],lazy[N],size[N],v[N],f[N]; 28 int ans[N][2]; 29 int n,m; 30 struct ac 31 { 32 int l,id,z,type; 33 }q[N]; 34 inline bool cmp(const ac &a,const ac &b) {return a.l<b.l;} 35 inline bool isroot(int x) {return c[fa[x]][0]!=x&&c[fa[x]][1]!=x;} 36 inline void update(int x) 37 { 38 int l=c[x][0],r=c[x][1]; 39 sum[x]=sum[l]+sum[r]+v[x]; 40 size[x]=size[l]+size[r]+1; 41 } 42 inline void solvelazy(int x,int y) 43 { 44 v[x]+=y; 45 lazy[x]+=y; 46 sum[x]+=y*size[x]; 47 } 48 inline void pushdown(int x) 49 { 50 int l=c[x][0],r=c[x][1]; 51 if(rev[x]) 52 { 53 rev[x]^=1;rev[l]^=1;rev[r]^=1; 54 swap(c[x][0],c[x][1]); 55 } 56 if(lazy[x]) 57 { 58 if(c[x][0]) solvelazy(c[x][0],lazy[x]); 59 if(c[x][1]) solvelazy(c[x][1],lazy[x]); 60 lazy[x]=0; 61 } 62 } 63 inline void rotate(int x) 64 { 65 int y=fa[x],z=fa[y],l,r; 66 if(c[y][0]==x)l=0;else l=1;r=l^1; 67 if(!isroot(y)) 68 { 69 if(c[z][0]==y) c[z][0]=x; 70 else c[z][1]=x; 71 } 72 fa[y]=x;fa[x]=z;fa[c[x][r]]=y; 73 c[y][l]=c[x][r],c[x][r]=y; 74 update(y),update(x); 75 } 76 inline void splay(int x) 77 { 78 int top=0;st[++top]=x; 79 for(int i=x;!isroot(i);i=fa[i]) st[++top]=fa[i]; 80 for(int i=top;i;i--) pushdown(st[i]); 81 while(!isroot(x)) 82 { 83 int y=fa[x],z=fa[y]; 84 if(!isroot(y)) 85 { 86 if(c[y][0]==x^c[z][0]==y) rotate(x); 87 else rotate(y); 88 } 89 rotate(x); 90 } 91 } 92 inline void access(int x) 93 { 94 int t=0; 95 while(x) 96 { 97 splay(x); 98 c[x][1]=t; 99 t=x;update(x);x=fa[x]; 100 } 101 } 102 inline void rever(int x) {access(x);splay(x);rev[x]^=1;} 103 inline void lnk(int x,int y) {rever(x);fa[x]=y;} 104 inline int query(int x,int y) {rever(x);access(y);splay(y);return sum[y];} 105 inline void add(int x,int y) {rever(x);access(y);splay(y);lazy[y]++;v[y]++;sum[y]+=size[y];} 106 main() 107 { 108 n=gi();m=gi(); 109 int l,r,tot=0,z; 110 for(int i=2;i<=n;i++) f[i]=gi(),f[i]++,lnk(i,f[i]); 111 for(int i=1;i<=m;i++) 112 { 113 l=gi(),r=gi(),z=gi(); 114 l++;r++;z++; 115 q[++tot].l=l-1,q[tot].id=i,q[tot].z=z;q[tot].type=0; 116 q[++tot].l=r,q[tot].id=i,q[tot].z=z;q[tot].type=1; 117 } 118 sort(q+1,q+1+tot,cmp); 119 int head=1; 120 for(int i=1;i<=tot;i++) 121 { 122 while(head<=q[i].l) add(1,head),head++; 123 ans[q[i].id][q[i].type]=query(1,q[i].z); 124 } 125 for(int i=1;i<=m;i++) printf("%lld\n",(ans[i][1]-ans[i][0])%mod); 126 return 0; 127 }



