机器学习之算法模型评价指标
机器学习评价指标
1、几个概念
精确率:Precision——”正确被检索的item(TP)”占所有”实际被检索到的(TP+FP)”的比例
召回率:Recall——“正确被检索的item(TP)”占所有”应该检索到的item(TP+FN)”的比例
F-measure= 正确率 * 召回率 * 2 / (正确率 + 召回率) (F 值即为正确率和召回率的调和平均值)
准确率:Accuracy—–正确分类的样本数与总样本数之比 。
2、AUC
AUC是一个模型评价指标,用于二分类模型的评价。AUC是“Area under Curve(曲线下的面积)”的英文缩写,而这条“Curve(曲线)”就是ROC曲线(也叫做受试者工作特征曲线)。
为什么要用AUC作为二分类模型的评价指标呢?为什么不直接通过计算准确率来对模型进行评价呢?
答案是这样的:机器学习中的很多模型对于分类问题的预测结果大多是概率,即属于某个类别的概率,如果计算准确率的话,就要把概率转化为类别,这就需要设定一个阈值,概率大于某个阈值的属于一类,概率小于某个阈值的属于另一类,而阈值的设定直接影响了准确率的计算。
例如:
数据集一共有5个样本,真实类别为(1,0,0,1,0);
二分类机器学习模型,得到的预测结果为(0.5,0.6,0.4,0.7,0.3)。
将预测结果转化为类别——预测结果降序排列,以每个预测值(概率值)作为阈值,即可得到类别。
'''
真实类别为(1,0,0,1,0);
预测结果为(0.5,0.6,0.4,0.7,0.3)
'''
1、当阈值 >=0.5 类别为1,否则为0
预测结果 准确率
[1,1,0,1,0] = 0.8
2、阈值 >=0.4 --->1
[1,1,1,1,0] -->0.6
3、阈值 > 0.6 --->1
[0,0,0,1,0] -->0.8
可以看出阈值的设定直接影响了准确率的计算。使用AUC可以解决这个问题,接下来详细介绍AUC的计算。
计算每个阈值下的“True Positive Rate”、“False Positive Rate”。以“True Positive Rate”作为纵轴,以“False Positive Rate”作为横轴,画出ROC曲线,ROC曲线下的面积,即为AUC的值。
那么什么是“True Positive Rate”、“False Positive Rate”?
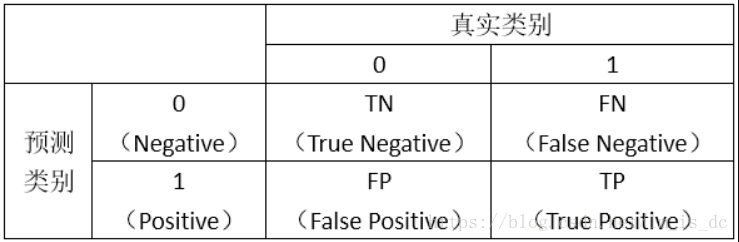
首先,我们看如下的图示:
0:负样本
1:正样本
表格对角线的值都是正确预测的值。
然后,我们计算两个指标的值:
TruePositiveRate = TP/(TP+FN),
代表将真实正样本划分为正样本的概率
FalsePositiveRate = FP/(FP+TN),
代表将真实负样本划分为正样本的概率
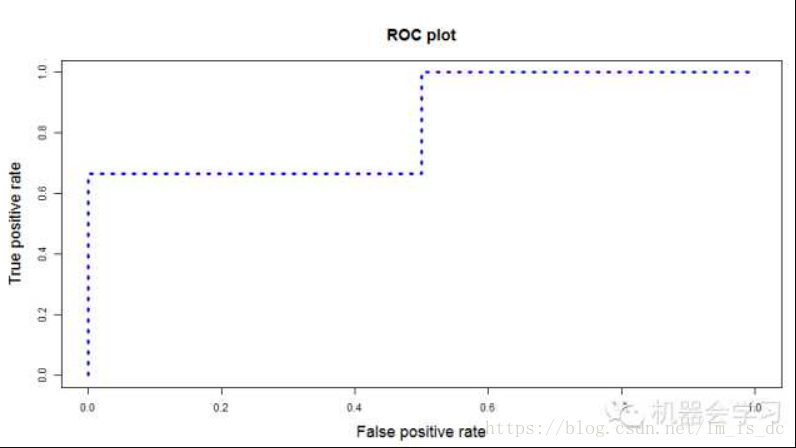
接着,我们以“True Positive Rate”作为纵轴,以“False Positive Rate”作为横轴,画出ROC曲线。类似下图:
ROC曲线下的面积,即为AUC的值,越大,说明模型预测效果越好。
- TPR:真实的正例中,被预测正确的比例
- FPR:真实的反例中,被预测正确的比例
最理想的分类器,就是对样本分类完全正确,即FP=0,FN=0。所以理想分类器TPR=1,FPR=0。
参考:https://blog.csdn.net/Csuriwolf/article/details/79143548
3、案例
导包
#逻辑斯蒂算法
from sklearn.linear_model import LogisticRegression
#支持向量机SVC算法
from sklearn.svm import SVC
#鸢尾花数据集
from sklearn.datasets import load_iris
#显示
from IPython.display import display
#auc曲线面积评价算法指标
from sklearn.metrics import auc,roc_curve
#线性插值
from scipy import interp
# 对数据进行划分,类似train_test_split
# 按照比例(目标值的比例)进行划分
from sklearn.model_selection import StratifiedKFold,KFold
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline获取数据
#获取数据 鸢尾花
iris = load_iris()
X = iris.data
y = iris.target
np.unique(y).size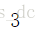
鸢尾花有3个类别.
把鸢尾花变成二分类问题,需要去掉一个类别.
#鸢尾花有3个类别
#把鸢尾花变成二分类问题,需要去掉一个类别
X = X[y!=2]
y = y[y!=2]
X.shape#鸢尾花的特征属性只有4个
#给鸢尾花增加特征属性,增加800个符合正态分布的数值
X = np.concatenate([X,np.random.randn(100,800)],axis=1)
X.shape线性插值示例
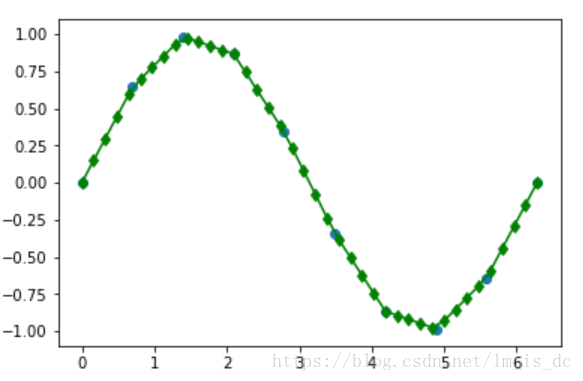
scipy包中的interp
在给定的10个点中插入40个点
#10个点
a = np.linspace(0,2*np.pi,10)
b = np.sin(a)
plt.scatter(a,b)
#线性插值 40个点
c = np.linspace(0,2*np.pi,40)
d = interp(c,a,b)
plt.plot(c,d,color = 'green',marker='d')StratifiedKFold和KFold数据切分示例
#使用KFold拆分数据
#X1 8个样本数据
X1 = np.array([
[1,2,3,4],
[11,12,13,14],
[21,22,23,24],
[31,32,33,34],
[41,42,43,44],
[51,52,53,54],
[61,62,63,64],
[71,72,73,74]
])
#8个目标数据
y1=np.array([1,1,0,0,1,1,0,0])
#一个样本数据对应一个目标值
#对数据分成4类
kFold = KFold(4)
for train,test in kFold.split(X1,y1):
# train,test代表索引
print(train,test)
#训练数据6个,测试数据2个StratifiedKFold:分层采样交叉切分,确保训练集,测试集中各类别样本的比例与原始数据集中相同.
sKFold = StratifiedKFold(4)
for train,test in sKFold.split(X1,y1):
# train,test代表索引
print(train,test)
#训练数据6个,测试数据2个使用SVC算法
#分层采样交叉切分,
#确保训练集,测试集中各类别样本的比例与原始数据集中相同
# 使用6折交叉验证,并且画ROC曲线
sKFold = StratifiedKFold(6)
#probability=True 显示概率
svc = SVC(kernel='linear',probability=True)
#求解 auc平均值
aucs = []
#横坐标0到1,分成100分
fpr_mean = np.linspace(0,1,100)
tprs = []
# train,test,是划分后的索引
#第几类标记
i = 1
for train,test in sKFold.split(X,y):
#根据索引从X和y中取出训练数据,训练模型
svc.fit(X[train],y[train])
#获取预测的概率分布
y_ = svc.predict_proba(X[test])
# print(y_)
# ROC曲线
#y_[:,1] 比较正样本 thresholds:阈值
fpr,tpr,thresholds = roc_curve(y[test],y_[:,1])
#不同的阈值,fpr和tpr的值就会不同
# print(thresholds)
# print(fpr)
# print(tpr)
# print('---------------------------------------')
#计算ROC曲线围成的面积
auc_ = auc(fpr,tpr)
aucs.append(auc_)
#线性插值 fpr和tpr只有几个值
#根据fpr_mean的值,插出tpr的值
tpr_mean = interp(fpr_mean,fpr,tpr)
tprs.append(tpr_mean)
#绘图
plt.plot(fpr,tpr,
label = 'Fold %d auc:%0.4f'%(i,auc_),alpha=0.3)
i += 1
#tprs有6个值,取其平均值
tpr_mean = np.mean(tprs,axis=0)
#tpr的值范围为0到1
tpr_mean[0] = 0
tpr_mean[1] =1
#计算平均面积
auc_mean = auc(fpr_mean,tpr_mean)
#求aucs方差
auc_std = np.std(aucs)
plt.plot(fpr_mean,tpr_mean,
label='Mean_auc:%0.4f$\pm$%0.2f'%(auc_mean,auc_std),
# $\pm$ 显示加减号
color='green')
#显示图例
plt.legend()结论:使用SVC模型对鸢尾花进行二分类的AUC面积为0.88,方差为0.08.



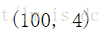


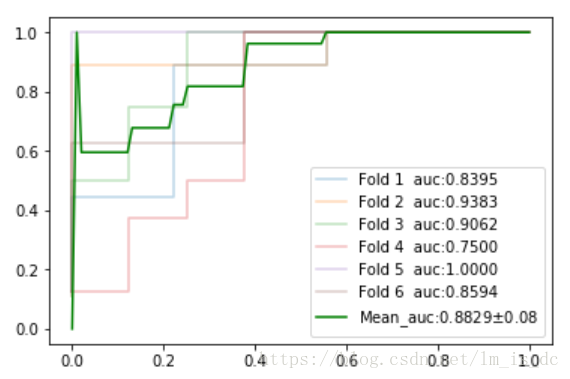

 浙公网安备 33010602011771号
浙公网安备 33010602011771号