ACM ICPC 2018 青岛赛区 部分金牌题题解(K,L,I,G)
目录:
————————————————————
ps:楼主脑残有点严重,很容易写错别字和语言组织混乱,如果在读文章时遇到,可以在评论区里回复一下,我好改(花式骗评论)
补题地址:http://acm.zju.edu.cn/onlinejudge/showProblems.do?contestId=1&pageNumber=31
顺便好人做到底,给大家凑个11/13的题解出来。(据说A题题解某个大佬是有写的,但是我找不到,有没有好心人告诉我一下)
B:https://www.cnblogs.com/xseventh/p/9986194.html(摸鱼的队员终于把B题补掉了,dsu on tree)
C:https://blog.csdn.net/lzyws739307453/article/details/83932183 (分类讨论)
D:https://blog.csdn.net/LSD20164388/article/details/83893264(枚举+讨巧)
E:https://blog.csdn.net/Code92007/article/details/83932020(二分+贪心)
F:http://www.cnblogs.com/qq965921539/p/9905086.html (构造题)
J :https://blog.csdn.net/Code92007/article/details/83930044(贪心)
M:傻逼签到题,递归到1时判奇偶就行了
____________________________
K Airdrop
虽然K题现场过的比较少,但实际上是一个排个序 ,按顺序枚举x0,大力数数的垃圾题,只是现场榜歪没人看而已。emmmm,根据重现的结果,可能k确实有一点难度,这里给一下提示,首先这个人啊,是优先先动y,再动x的,所以不和x=x0在同一条线上的点,只要与(x0,y0)的曼哈顿距离相同就有可能会撞。因此我们要在(x0,y0)的左右两边分别数每种曼哈顿距离出现的次数。显然左右的是可以拆开数,所以我们先把所有x0左侧曼哈顿距离相同的点的数量数完,在数右边,最后在数一下多少个点的x=x0就行,如果你有注意到题目有说所有点的初始位置是不一样的,可能会好写很多。
现在以数左边曼哈顿距离相同的点的数量为例,首先要注意到什么情况下曼哈顿距离相同点并不会抵消掉而是会留下一个,这里举个栗子,当有三个点对于(x0,y0)的曼哈顿距离相同时,万一有两个因为比较早相遇而挂掉,则最后一个人就能活到空投那里。解决办法也简单,注意到,他们只能在y=y0这条直线上相遇,早相遇的点,他们相遇的x也比较小,只要在从左往右枚举x0的过程中,顺便把在上个x0的相撞死的人对于的数量贡献去掉就好了。再维护一下当前有多少个曼哈顿距离只出现了1次,只出现一次的点都是能活着到空投的。
最后的最后,在教一下怎么数量,因为对于不同的x0,y0所有点的曼哈顿距离都在变的,我们不能每次重新数所有距离出现的次数。但是对于在(x0,y0)左侧点,如果他们对于(x0,y0)曼哈顿距离相同,随着(x0,y0)右移他们还是会相同的,所以干脆直接数他们到(xm,y0)的曼哈顿距离就行了,xm为x0坐标的最大值。 他们到(xm,y0)距离相同的话,则这些点到任意他们的右侧(x0,y0)距离也肯定相同。

1 #include<stdio.h> 2 #include<math.h> 3 #include<string.h> 4 #include<stdlib.h> 5 #include<vector> 6 #include<algorithm> 7 using namespace std; 8 int const maxn=2e5+5; 9 int x[200005]; 10 int y[200005]; 11 vector<int>e[maxn],q,que,res; 12 int sum[200005]; 13 int num[200005]; 14 void clear(int n,int x0,int y0) 15 { 16 for(int i=1;i<=n;i++) 17 { 18 num[abs(x0-x[i])+abs(y0-y[i])]=0; 19 } 20 } 21 int main() 22 { 23 int i,j,n,m,w,t,y0,xm=1e5+1,k; 24 scanf("%d",&t); 25 while(t--) 26 { 27 scanf("%d%d",&n,&y0); 28 q.clear(); 29 q.push_back(0); 30 // e[0].clear(); 31 for(i=1;i<=n;i++) 32 { 33 scanf("%d%d",&x[i],&y[i]); 34 e[x[i]].clear(); 35 e[x[i]+1].clear(); 36 // e[x[i]-1].clear(); 37 q.push_back(x[i]); 38 q.push_back(x[i]+1); 39 // q.push_back(x[i]-1); 40 } 41 sort(q.begin(),q.end()); 42 q.erase(unique(q.begin(),q.end()),q.end()); 43 for(i=1;i<=n;i++) 44 { 45 e[x[i]].push_back(y[i]); 46 } 47 int ans=0,temp=0; 48 clear(n,xm,y0); 49 for(int xx:q) 50 { 51 sum[xx]=e[xx].size(); 52 if(temp) 53 { 54 que.clear(); 55 for(int yy:e[temp]) 56 { 57 k=abs(yy-y0)+abs(xm-temp); 58 num[k]++; 59 if(num[k]==1) 60 { 61 ans++; 62 } 63 else 64 { 65 que.push_back(k); 66 } 67 } 68 for(int pos:que) 69 { 70 if(num[pos]) 71 ans--; 72 num[pos]=0; 73 } 74 } 75 temp=xx; 76 sum[xx]+=ans; 77 // printf("(%d %d)\n",xx,sum[xx]); 78 } 79 reverse(q.begin(),q.end()); 80 81 ans=0,temp=0; 82 clear(n,0,y0); 83 res.clear(); 84 for(int xx:q) 85 { 86 if(temp) 87 { 88 que.clear(); 89 for(int yy:e[temp]) 90 { 91 k=abs(yy-y0)+abs(0-temp); 92 num[k]++; 93 if(num[k]==1) 94 { 95 ans++; 96 } 97 else 98 { 99 100 que.push_back(k); 101 } 102 } 103 for(int pos:que) 104 { 105 if(num[pos]) 106 ans--; 107 num[pos]=0; 108 } 109 } 110 temp=xx; 111 sum[xx]+=ans; 112 res.push_back(sum[xx]); 113 //printf("(%d %d %d)\n",xx,sum[xx],ans); 114 } 115 sort(res.begin(),res.end()); 116 printf("%d %d\n",res.front(),res.back()); 117 } 118 return 0; 119 }
I Soldier Game
这题两种写法,一种是枚举最小值+线段树单点更新维护可行最大值。 另一种是dp (神仙知道怎么写,我不知道)。这题思路还是比较复杂了,然后HDU的CSY巨巨现场一眼标算,果然神仙和凡人是不能比的。
当我问群巨怎么做时,他们只给我“枚举最小值+线段树维护可行最大值“,这几个关键字,我百思不得其解,终于想了几天后顿悟了。o(╥﹏╥)o
首先。我们考虑一个动态规划问题:给出a个长度为1的区间和b个长度为2区间,每个区间都有权重。从中取出若干个不相交的区间,在满足覆盖满[1,n]情况下,使得【权重最大的区间】的权重最小,要怎么做。
一个显然的想法:令dp[i]代表覆盖满[1,i]的所有方案中,权重的最大值最小为多少。然后按左端点从小到大枚举区间,进行状态转移就行了,复杂度O(a+b)。
然后现在我就可以得到I题的一个O(n^2)写法了,具体做法是这样的:
我们把n个长度为1的区间和n-1长度为2的区间按权值排序 ->枚举最小值 -> 将权值小于最小值的区间删去 ->
-> 然后对剩下的区间做dp,求出可行的【最小的最大值】,计算最大值和当前枚举的最小值之差,并更新答案。
上面那个做法虽然不够优越,但是已经为正确的做法已经铺好了路,因为上面涉及到一个线性dp的单点修改后在查询,套个老掉牙线段树维护dp值不就可以在log(n)的时间内查询到修改后的值了吗。
所以现在我们就有了个nlog(n)做法,核心在于怎么把dp挂到线段树上。不过说起来容易做起来难, 因为你发现如果你要搬到线段树上要维护一坨东西才行,
不过核心思想并不复杂,只是枚举一下树上孩子合并时是否有区间跨过两个孩子就行了,合并操作的具体代码长这样
1 struct Node 2 { 3 ///m代表中间,l代表左,r代表右 4 int rl; 5 int m;///只包含中间,不包含区间的左右端点 6 int mr;///包含中右 7 int lm;///包含左中 8 int lmr;///包含左中右 9 int set(int i) 10 { 11 rl=a[i][1]; 12 lm=mr=-INF; 13 lmr=a[i][0]; 14 m=INF; 15 } 16 inline Node operator+(const Node &b)const 17 { 18 Node ans; 19 ans.m=min(max(mr,b.lm),max(max(m,rl),b.m)); 20 ans.lm=min(max(lmr,b.lm),max(max(lm,rl),b.m)); 21 ans.mr=min(max(mr,b.lmr),max(max(m,rl),b.mr)); 22 ans.lmr=min(max(lmr,b.lmr),max(max(lm,rl),b.mr)); 23 ans.rl=b.rl; 24 return ans; 25 } 26 27 };
有没有被吓到,不过努力思考一下应该还是看得懂的。
完整的AC代码如下(我删掉一个区间的方法,是把这个区间权值赋值成无穷大,这样对答案就没有贡献了,话说我居然是跑得最快的╰(*°▽°*)╯):

1 #include<stdio.h> 2 #include<string.h> 3 #include<algorithm> 4 #include<math.h> 5 using namespace std; 6 typedef long long ll; 7 #define N 280000 8 int a[200005][2]; 9 const int INF=(1<<31)-1; 10 struct Node 11 { 12 ///m代表中间,l代表左,r代表右 13 int rl; 14 int m;///只包含中间,不包含区间的左右端点 15 int mr;///包含中右 16 int lm;///包含左中 17 int lmr;///包含左中右 18 int set(int i) 19 { 20 rl=a[i][1]; 21 lm=mr=-INF; 22 lmr=a[i][0]; 23 m=INF; 24 } 25 inline Node operator+(const Node &b)const 26 { 27 Node ans; 28 ans.m=min(max(mr,b.lm),max(max(m,rl),b.m)); 29 ans.lm=min(max(lmr,b.lm),max(max(lm,rl),b.m)); 30 ans.mr=min(max(mr,b.lmr),max(max(m,rl),b.mr)); 31 ans.lmr=min(max(lmr,b.lmr),max(max(lm,rl),b.mr)); 32 ans.rl=b.rl; 33 return ans; 34 } 35 36 }; 37 const int MAXN=280000; 38 struct Segment_tree 39 { 40 int size; 41 Node node[MAXN]; 42 void update(int pos) 43 { 44 node[pos]=node[pos+pos]+node[pos+pos+1]; 45 } 46 void build(int n)///申请空间 47 { 48 size=1; 49 while(size<n)///计算几个刚好能套住整个区间的区间容量 50 size<<=1;///size=size*2 51 // printf("size=%d\n",size); 52 } 53 void build(int n,int flag)///申请空间,并建树 54 { 55 build(n); 56 int i; 57 for(i=n; i<size; i++) 58 { 59 a[i][0]=-INF; 60 a[i][1]=INF; 61 } 62 for(i=0; i<size; i++) 63 { 64 node[size+i].set(i); 65 } 66 for(i=size-1; i>0; i--) 67 { 68 update(i);///数值从低到高更新上去 69 } 70 } 71 void change(int x) 72 { 73 x+=size; 74 node[x].set(x-size); 75 while(x>1) 76 { 77 // printf("[%d]\n",x); 78 x>>=1; 79 update(x); 80 } 81 } 82 void put() 83 { 84 int i=1,j=1,s=size*4,k,len=3; 85 for(i=1; i<=2*size-1; i++) 86 { 87 if(i==j) 88 { 89 puts(""); 90 j<<=1; 91 s>>=1; 92 for(k=0; k<len*(s/2-1); k++) 93 printf(" "); 94 } 95 printf("%3d",node[i].lmr); 96 for(k=0; k<len*(s-1); k++) 97 printf(" "); 98 } 99 puts(""); 100 } 101 102 } tree; 103 typedef pair<int,int> PI; 104 PI b[200005]; 105 int cmp(const PI &x,const PI &y) 106 { 107 return a[x.first][x.second]<a[y.first][y.second]; 108 } 109 int main() 110 { 111 int n,m,t,i; 112 //freopen("1.in","r",stdin); 113 scanf("%d",&t); 114 while(t--) 115 { 116 scanf("%d",&n); 117 int top=0; 118 for(i=0; i<n; i++) 119 { 120 scanf("%d",&a[i][0]); 121 b[top++]=make_pair(i,0); 122 if(i>0) 123 { 124 a[i-1][1]=a[i-1][0]+a[i][0]; 125 b[top++]=make_pair(i-1,1); 126 } 127 } 128 a[n-1][1]=INF; 129 sort(b,b+top,cmp); 130 tree.build(n,1); 131 int j=0; 132 int mn; 133 long long ans=INF*2LL; 134 for(i=0; i<top;) 135 { 136 mn=a[b[i].first][b[i].second]; 137 // printf("i=%d\n",i); 138 139 if(tree.node[1].lmr==INF) 140 { 141 break; 142 } 143 ans=min(ans,tree.node[1].lmr-(long long)mn); 144 while(j<top&&a[b[j].first][b[j].second]<=mn) 145 { 146 a[b[j].first][b[j].second]=INF; 147 tree.change(b[j].first); 148 j++; 149 } 150 i=j; 151 } 152 153 printf("%lld\n",ans); 154 } 155 return 0; 156 }
L Sub-cycle Graph
好吧,这是一个比较傻吊的组合数学题,但是现场的时候看错条件了,越想越复杂_(¦3」∠)_。
题意是问有多少种n个点m条边的图,是一个连通简单环图的子图。
首先因为是连通简单环图,所以母图必须只有一个简单环且连通所有结点,在断掉一些边后,必然会变成n-m条链的组合。
现在我们先来考虑一个比较简单的问题:n个结点组成一条链有多少种本质不同的方案
显然这个数列的前n项是1,1,3,12,……,n!/2。
写成Σai/(i!) x^i 的指数型生成函数的话(什么你不会指数型生成函数,那还不赶紧去学),就是
则组成k条链的指数型生成函数就是
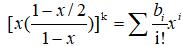
则题目想要的答案就是bn /k!。 为啥除k! ? 因为我们的答案是不考虑这k条链出现的先后顺序的。
然后开始FFT?, 答案是NO!
上面那个多项式我们并不需要真的做多项式的幂运算。首先上面的式子可以拆成这样。
其中
可以用二项式系数直接展开。
而
是一个特殊的多项式,与这个多项式做卷积相当于对系数求前缀和。
乘k次,就相当于求k次前缀和,求k次前缀和的第m项,想必现在是个人都应该会了。
所以到此题目就做完了,算法复杂度O(m)

1 #include<stdio.h> 2 #include<algorithm> 3 using namespace std; 4 #define ll long long 5 ll fac[100005],ifac[100005]; 6 const ll mod=1e9+7,inv2=(mod+1)/2; 7 ll C(int n,int m) 8 { 9 if(m>n) 10 return 0; 11 return fac[n]*ifac[m]%mod*ifac[n-m]%mod; 12 } 13 int main() 14 { 15 int n=1e5+2,m,t,i,j,k; 16 ifac[1]=1; 17 ifac[0]=1; 18 for(i=2; i<=n; i++) 19 { 20 ifac[i]=(mod-mod/i)*ifac[mod%i]%mod; 21 } 22 fac[0]=1; 23 for(i=1; i<=n; i++) 24 { 25 fac[i]=fac[i-1]*i%mod; 26 ifac[i]=ifac[i-1]*ifac[i]%mod; 27 } 28 scanf("%d",&t); 29 while(t--) 30 { 31 scanf("%d%d",&n,&m); 32 if(m>n) 33 { 34 puts("0"); 35 } 36 else if(m==n) 37 { 38 printf("%lld\n",fac[n-1]*inv2%mod); 39 } 40 else 41 { 42 ll ans=0,temp=1; 43 k=n-m; 44 for(i=0;i<=m;i++) 45 { 46 // printf("[%d %d],%d\n",k,m-i,C(k+(m-i)-1,m-i)); 47 ans+=C(k,i)*temp%mod*C(k+(m-i)-1,m-i)%mod; 48 ans%=mod; 49 temp=temp*-inv2%mod; 50 if(temp<0) 51 temp+=mod; 52 } 53 printf("%lld\n",ans%mod*fac[n]%mod*ifac[k]%mod); 54 } 55 56 } 57 return 0; 58 }
G Repair the Artwork
问题1:
只有0和1情况方案数怎么计算?
在只有0,1的时候,可行方案数显然 【可选的区间数】^m
问题2:
只有2的情况方案数怎么计算:
为了方便表示,我们约定一下记号(不然说起来会像绕口令)
- 如果一个位置上的2被当做1用(即一定不覆盖这个位置)我们把用×表示这个2,
- 如果一个位置上的2被当做0用(即这个位置可能被覆盖,也可能没有被覆盖)我们把用O表示这个2。
- 如果一个位置上的2一定被覆盖用Θ表示,
- {??……?} 表示每个2满足??……?约束情况下的方案数。
现在我们来推导一下只有两个2时方案数怎么计算
则我们要求的答案{ΘΘ},随便容斥一下就可展开成如下形式:
(注:如果你实在看不懂,我再解释一下,{OΘ}可以拆成第一个位置【一定被被覆盖】和【一定不被覆盖】两种情况,所以就有了{OΘ}={ΘΘ}+{×Θ} =>{ΘΘ}={OΘ}-{×Θ}. 接着同理对剩下的Θ,用相同的方式展开掉就行了。}
这样就转化为只有01的形式,然后用问题的1方式就能计算了,到这问题就解决了吗?然而还有一些计算上的细节问题要解决。
所以我们继续尝试计算{ΘΘΘ},来说明这个问题
经过一番费力的展开,你会得到{ΘΘΘ}={OOO} - {OO×} - {O×O} + {O××} - {×OO} + {×O×} + {××O} -{×××} .
你观察一下就会发现,实际上发现,其实就是

其中r(A1,A2,A3) 为A1,A2,A3中x的个数。 说白就是类似多项式(1+(-x))^m 的展开形式。
在这里我们有两个重要的结论:
- 结论一:答案一定能表示如下形式(因为任意一个{A1,A2,A3}肯定是x^m 形式)。

- 结论二:暴力枚举情况,要枚举2^n种可能,所以暴力是不可行的
问题3:在只有2的情况下,怎么在多项式时间里计算n个2的方案数?
根据问题2的结论1,对dp初步方案是用dp[i][j],代表{i个Θ}中 j^m的系数。 然后答案就是Σdp[i][j]* j^m,
然后来考虑一下转移:{i个Θ}={(i-1个Θ) +O}-{i-1个Θ) +×}。
你自行思考一下就会发现,这个{ (i-1个Θ) +×} 不就是等于{i-1个Θ} 吗? 因为这个尾巴上的×,对可选区间数莫有虾米贡献,(因为x是不能选的,挂不挂在尾巴上没差)。
而这个(i-1个Θ) +O} 好像不太能转化成和{i-1个Θ}有关形式,因为每种情况的可选区间数,都可以额外增加【最后一个O贡献的可选区间的数】=【右端点为n的可选区间的数量】=【i - 上一个1的位置】。但是这个上一个1的位置,对于不同情况是不一样的。(例如{OO}=3^m 而再加个O话,{OOO}=(3+3)^m ,而对于{O×}=1^m,再加个O,{O×O}=(1+1)^m,)
因此我还需要对dp状态加个维度,我们用dp[i][j][k]代表{i个Θ}展开中,最后一个×出现的位置为j的方案中 k^m的系数。 然后答案就是Σdp[i][j][k]* k^m,
现在我在来考虑一下dp方程这么转移。我们要加上{(i-1个Θ) +O}的方案数,减掉{i-1个Θ) +×}的方案数,所以有:
- 当尾巴加O不改变最后一个1位置,但是改变可选区间数:
for(j=0,j<i;j++)
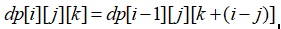
- 当尾巴加x时,所有转移到这个状态的,【最后一个1的位置】都要改成i:
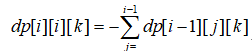
到此转移就完成了,然后你会发现,这个算法是n^4。但是常数很小,然后题目有1000组数据,其中包含50组大数据_(¦3」∠)_,写挫就可能惨遭卡常。
顺便给个样例,100个2 ,m=1e9 的方案数mod 1e9+7 的结果是388544367。
问题四 在0,1,2三种数字都考虑的情况,状态该怎么转移?。
其实0,1转移方法和上面类似的,
- 所以遇到1,因为{(i-1个Θ) +1}={(i-1个Θ) } ,所以连动都不要动,但是注意需要记这个1的位置,因为在计算右端点为n的可选区间的数量会用到。
- 而遇到0时,所有情况下k那个维度都要加上【i - 上一个1的位置】偏移量,所以要讨论一下这个1是从2变来,还是真正的1。
- 然后遇到2,转移是和问题三一样的,只不过也要注意一下,计算偏移量时的这个1是从2变来,还是真正的1就行了
最后,你发现这个毒瘤题还会有爆内存的风险,需要优化掉一维的空间。而且可能还要和卡常斗智斗勇。
所以再仔细观察一下,你发现这两种转移其实就是两种简单的操作:一种是数组下标偏移,一种是求j那维的前缀和。
因此当个二维数组写的时候:遇到1,不做任何操作。遇到0时只累加偏移量。遇到2,枚举j求个前缀和,求玩在计算2带来的偏移量。
最后在计算答案的时候,把偏移量代入就行了
AC代码如下:

1 #include<cstdio> 2 #include<algorithm> 3 #include<string.h> 4 #include<vector> 5 using namespace std; 6 #define ll long long 7 const int mod=1e9+7; 8 inline int max(const int &x,const int &y) 9 { 10 return x>y?x:y; 11 } 12 int dp[105][6005]; 13 int d[105]; 14 int xx[105]; 15 int a[105]; 16 ll temp[6005]; 17 inline ll quickpow(ll a, ll n) 18 { 19 ll ans=1; 20 while(n) 21 { 22 if(n&1) 23 ans=ans*a%mod; 24 n>>=1; 25 a=a*a%mod; 26 } 27 return ans; 28 } 29 int main() 30 { 31 int n,m,t,r,i,mx; 32 scanf("%d",&t); 33 while(t--) 34 { 35 scanf("%d%d",&n,&m); 36 r=0; 37 mx=0; 38 a[0]=2; 39 for(i=1; i<=n; i++) 40 { 41 scanf("%d",&a[i]); 42 if(a[i]==1) 43 { 44 r=i; 45 } 46 mx+=i-r; 47 } 48 for(i=0; i<=n; i++) 49 memset(dp[i],0,sizeof(dp[i][0])*(mx+1)); 50 memset(xx,0,sizeof(xx)); 51 memset(d,0,sizeof(d)); 52 dp[0][0]=1;///注意啥都不选也有一种方案。 53 r=0; 54 mx=0; 55 for(i=1; i<=n; i++) 56 { 57 if(a[i]==1)///1的时候屁事都不干 58 { 59 r=i; 60 } 61 else 62 { 63 if(a[i]==0)///0的时候累加偏移量 64 { 65 for(int j=0; j<i; j++) 66 { 67 xx[j]+=i-max(j,r); 68 } 69 } 70 else if(a[i]==2) 71 { 72 for(int j=0; j<i; j++) 73 { 74 if(a[j]==2) 75 { 76 mx=d[j]; 77 d[i]=max(d[i],mx+xx[j]);///d[i]是可能有值的系数的宽度。 78 for(register int k=xx[j]; k<=mx+xx[j]; k++)///这里注意一下j带有的偏移量,所以不能直接 dp[i][k]-=dp[j][k],而是应该dp[i][k]-=dp[j][k-xx[j]];, 79 { 80 dp[i][k]-=dp[j][k-xx[j]]; 81 if(dp[i][k]<0) 82 dp[i][k]+=mod; 83 } 84 } 85 } 86 for(int j=0; j<i; j++)///把2当0时累加偏移量。注意这个for是不能和上一个for交换位置,如果写个三维数组的,再改成二维数组就会知道为什么。 87 { 88 xx[j]+=i-max(j,r); 89 } 90 } 91 } 92 } 93 long long ans=0; 94 mx=0; 95 for(i=0; i<=n; i++) 96 { 97 mx=max(mx,d[i]+xx[i]); 98 } 99 for(i=1; i<=mx; i++)///预处理一下所有数的次幂。 100 { 101 temp[i]=quickpow(i,m); 102 } 103 for(int i=0; i<=n; i++) 104 { 105 if(a[i]==2) 106 { 107 for(int j=0; j<=d[i]; j++) 108 { 109 ans+=dp[i][j]*temp[j+xx[i]]%mod; 110 ans%=mod; 111 } 112 } 113 } 114 if(ans<0) 115 ans+=mod; 116 printf("%lld\n",ans); 117 } 118 return 0; 119 }





