杜教筛使用心得
现在杜教筛好像是个人都会了 orz。
所以我写篇博客复习一下，这里不讲原理只讲优化技巧的和如何使用
先贴两个学习原理的博客：
http://www.cnblogs.com/abclzr/p/6242020.html
http://www.cnblogs.com/candy99/p/dj_s.html
然后我们来讲一下，怎么使用，下面均以要 求和的n为109 为讨论前提
常用公式
一般取用来卷积的辅助函数g为恒等函数：g(n)=1 ,n=1,2,3,…………（有时取g(n)=mu(n) 啥的也有奇效，反正是玄学）
这时杜教筛的公式就能化简为：
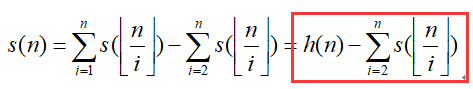
我们一般只用红框里的两个公式。
杜教筛不要求函数一定要有积性，而是要求两点
- f(i)在106以内的所有前缀和能在接近O(n)复杂度内全部处理出来。
- 狄利克雷卷积的前缀和——h(n) ，在1e9 内的任意一项h(m)，能在O(sqrt(m)) 以内的复杂度内求出来。
使用步骤一：预处理106 以内的s[i]
这一步如果f(i)是积性函数，可以直接用线性筛法直接搞定，如果不是的话，就要可能要注意分析性质瞎搞了(比如搞一些预处理，使得f(i)可以O(1)求之类的骚操作)。
注意这里只是以106为例，因为后面的计算过程常数比较大，追求速度的话，最好要能处理到2*106。
使用步骤二：写快速计算h函数第k项的函数 h(int k)
这里求h，有以下几种方法
-
用公式推出
的通项看是否有优良的性质。可以快速搞出前n项和 - 对打表找规律
- 对
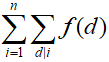打表找规律
使用步骤三：写个记忆化搜索计算s(n)
设我们预处理出s[i]的范围是i∈[1,UB】。
通用的写法
若之前算过n 我们则返回我们记下的值，因为n比较大不能用数组直接存，最好用哈希表。
若n<=UB,我们返回预处理好的s[i]
否则使用公式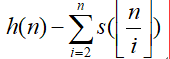
递归计算
要注意到(n/i) 只有2*sqrt(n) 不同的取值，直接用一下数论分块就行了（如果不知道啥是数论分块的话，你百度一下就行 了）
然后注意把值存到哈希表内。
代码如下
1 long long S(long long n) 2 { 3 if(n<=UB) 4 { 5 return s[n]; 6 } 7 long long ans=0; 8 ans=table.find(n);///查询哈希表中是否有n 9 if(ans==-1) 10 { 11 long long i,j; 12 ans=0; 13 for(i=2; i<=n; i++) 14 { 15 j=i; 16 i=n/(n/i); 17 ans+=(i-j+1)*S(n/j); 18 } 19 ans=(h(n)-ans); 20 table.insert(n,ans);/// 将n对应的值存入哈希表 21 } 22 return ans; 23 }
更方便的写法
但是如果只有单组，或者你不最求速度，这里有通过构造一个完美哈希把哈希表扔掉，且非递归的写法。
首先我发现递归的时候是从大递归到小的，跟dp原理递推的方法一样，我可以反过来从小算到大，这样就能保证每次转移时子状态已经算好了。
然后问题的关键在于有多少种不同状态，可以发现递归时，n是不断被除的，当前状态即x=n /a1/a2/a3/……/ak 这到底会有多少种不同的取值呢？ 答案是2*sqrt(n)
因为可以证明在取整情况下也满足 x=n /a1/a2/a3/……/ak = n/(a1*a2*a3*……*ak) 即x=n/m 而n/m在取整的情况下 就2*sqrt(n)种不同的取值.
接着因为我们预处理了n^(2/3) 即106内的结果， 我们可以再扔掉一部分状态，只留n^(1/3)的状态用公式计算出来就行了。
到这里,因为每次转移复杂度是2*sqrt(x)的，可以证明出杜教筛的复杂度是
※提取要计算的状态
好废话讲了那么多，我们先预处理出，所要计算的n^(1/3)的状态的位置（即（n/1,n/2,n/3,……n/(1e3)））
这里直接用暴力算出来就行，代码如下，注意要按大小顺序存起来方便后面转移
1 vector<ll>q; 2 for(int i=1; i<=n; i++) 3 { 4 i=n/(n/i); 5 if(n/i<=UB) 6 break; 7 q.push_back(n/i); 8 }
※构造完美哈希算法
这里只要一行代码，就可以构造出完美哈希从而扔掉哈希表，然后把s数组多开大sqrt(n)的大小就行了，其中的原理和精髓可看最终代码
#define id(x) x<=UB?x:(n/(x)+UB)
注：这里可以证明若UB>sqrt(n),对于所有大于UB的x。n/x 的取值一对一映射到[1,n/UB] 区间内
※最终的实现方式
最后总体代码如下
1 ll cal(ll n) 2 { 3 vector<ll>q; 4 for(int i=1; i<=n; i++) 5 { 6 i=n/(n/i); 7 if(n/i<=UB) 8 break; 9 q.push_back(n/i); 10 } 11 int k; 12 ll ans,i,j,m,t; 13 for(k=q.size()-1; k>=0; k--)///从小到大枚举状态 14 { 15 ans=0; 16 m=q[k]; 17 for(i=2; i<=m; i++)///递推公式，和文章上面哈希表的写法对比一下就知道写的是什么了。 18 { 19 j=i; 20 t=(m/i); 21 i=m/t; 22 ans+=(i-j+1)*s[id(t)]; 23 } 24 ans=(h(m)-ans); 25 s[id(m)]=ans; 26 } 27 return s[id(n)]; 28 }
使用步骤四：验板子
你要想要知道自己板子有没写错，或者写搓怎么办？。上OJ验板子， 一直wa也不知道wa在哪，题目函数太复杂怎么办？
答：这里要用验筛法板子的神级函数，f(i)=i. 这个函数前n项和对1e9+7 取模的结果，用脚指头算都知道是 n*(n+1)/2%（1e9+7） ，很容易知道你板子算出来的结果对不对。中间过程也比较好处理。
- 首先步骤一：求s[i]前106项，这里我就不详细说明了，s[i]=s[i-1]+i
- 接着步骤二：写求h的函数,
，emmmmmmmmmmmm这东西能快速算？？？。 这里有一个只有s(n)很快速计算第n项时（要是能快速计算还写毛杜教筛，所以这个技巧没卵用，不过能用来验板子）才能使用的技巧——枚举d的取值，则有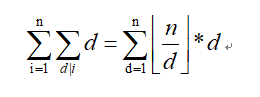
，在配合数论分块就能在根号复杂度内算出h(n)了 - 套上面步骤三写好的代码，注意加个取模
- 运行代码，从文件中读入1000000000。看程序的运行时间和计算结果
示例代码如下:
1 #include<stdio.h> 2 #include<string.h> 3 #include<vector> 4 #include<algorithm> 5 using namespace std; 6 #define ll long long 7 #define id(x) x<=UB?x:(n/(x)+UB) 8 const int UB=1e6; 9 const int N=100000; 10 const ll mod=1e9+7; 11 ll s[UB+N]; 12 void init()///预处理s的前UB项 13 { 14 for(int i=1;i<=UB;i++) 15 { 16 s[i]=s[i-1]+i; 17 s[i]%=mod; 18 } 19 } 20 ll h(ll n)///h=Σ Σf(d)*[i%d==0] h为狄利克雷卷积的前缀和 21 { 22 ll i,j; 23 ll sum=0; 24 for(i=1;i<=n;i++) 25 { 26 j=i; 27 i=n/(n/i); 28 sum+=(j+i)*(i-j+1)/2%mod*(n/i)%mod; 29 } 30 return sum%mod; 31 } 32 ll cal(ll n) 33 { 34 vector<ll>q; 35 for(int i=1; i<=n; i++) 36 { 37 i=n/(n/i); 38 if(n/i<=UB) 39 break; 40 q.push_back(n/i); 41 } 42 int k; 43 ll ans,i,j,m,t; 44 for(k=q.size()-1; k>=0; k--)///从小到大枚举状态 45 { 46 ans=0; 47 m=q[k]; 48 for(i=2; i<=m; i++)///递推公式，和文章上面哈希表的写法对比一下就知道写的是什么了。 49 { 50 j=i; 51 t=(m/i); 52 i=m/t; 53 ans+=(i-j+1)*s[id(t)]%mod; 54 } 55 ans=(h(m)-ans)%mod; 56 if(ans<0) 57 ans+=mod; 58 s[id(m)]=ans; 59 } 60 return s[id(n)]; 61 } 62 int main() 63 { 64 int i,j; 65 ll n=1e9; 66 // scanf("%lld",&n); 67 init(); 68 printf("out=%lld,ans=%lld\n",cal(n),(n*(n+1)/2)%mod); 69 return 0; 70 }
这个这个必须一秒内出来，且答案正确，不然你就凉拉
