梯度下降
梯度其实是一个向量,包含两个要素,大小和方向。其中方向是偏导数最大的那个方向,偏导数的最大值。
用数学来描述的话,就是。
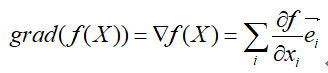
其中f一般是代价函数

而所谓梯度下降其实就是沿着梯度的反方向(函数值减少的最快的方向)移动一定的步长的迭代算法,通过一定次数的迭代后就可以快速的下降局部最小值周围。
而梯度下降一般用于严格凸函数,即只有一个极小值,且除最小值点外,其他点梯度不等于0。
其数学表达式是
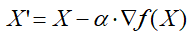
其中X是n维参数向量。α是学习因子,用于控制步长,一般初始值取0.1左右。
列1:
对于线性回归
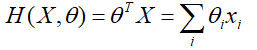
在数据集{Xi,yi}其代价函数为
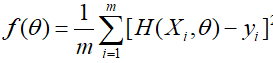
目标是求解出合适的参数θ,使得代价函数最小化。让f对θ求偏导和整理可以得到一个优雅的迭代方程
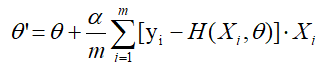
为啥这个方程优雅呢,因为这个方程可以这样表达:

我们发现更新量其实就是对拟合偏差的线性加权。
此外梯度下降还存在许多优化,比如学习因子的控制,初始值的选取




