虚树学习笔记

虚树算法其实原理蛮简单的就是，从一颗n个结点的原树上在只取出必要结点成一颗新树，这颗新树必包含指定m个结点并保持原树上的祖孙关系。

首先我们来解答一些问题

问：什么样的结点是必要的呢？？

答：指定的m个结点和 这m个结点中任意两个结点的最近公共祖先。

问：为啥要包含最近公共祖先呢？

答：因为最近公共是虚树的关节点，起到连接这m个点的作用

问：任意两个结点的公共祖先构成集合，会不会有m*(m-1)/2个点？

答：其实这些祖先构成的集合最多就m-1个点，因为虚树其实原理有点类似在树上跑不压缩路径的并查集，你连接m个点最多也只需要m-1个关节点.

首先来看两张图，直观感受虚树的构建

1.构建必须包含2,4,7,6的虚树

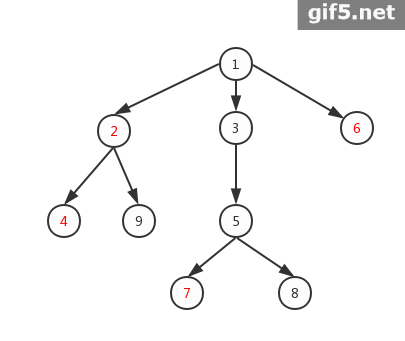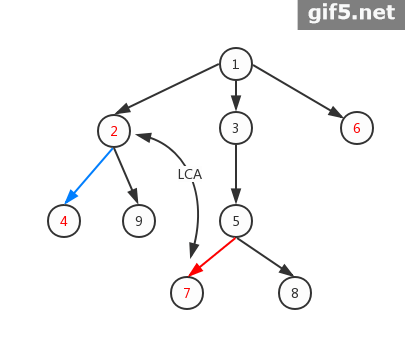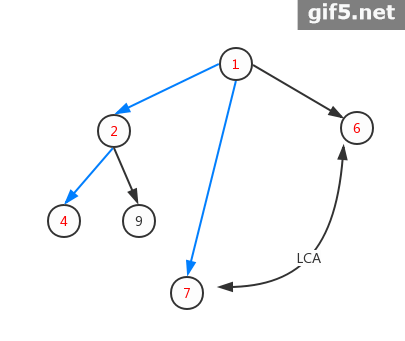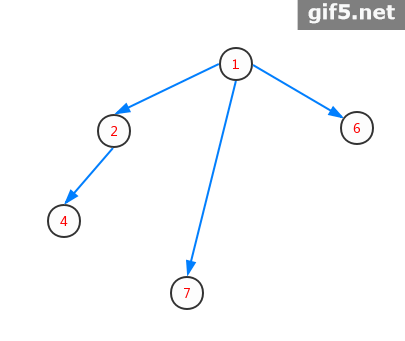
2.构建必须包含2,7,8的虚树

 

 虚树的构建方法可以看这篇文章https://www.cnblogs.com/chenhuan001/p/5639482.html

总体上就是先按dfs排个序，然后用栈加LCA对这m个结点实现深度优先遍历并记录路径以方便建虚树。最后要注意的是建边一定要在出栈的时候建，因为有可能出现图2的那种情况，两个点之间还需再塞进去一个结点。

算法复杂度：

因为虚树构建时需要对结点按dfs序排序，并求出排序后相邻结点的LCA的所以算法复杂度O(mlog(n*m))

虚树优点：

虚树主要配合树形DP食用，因为树形DP的复杂是与树的结点数成正比的，通过构建虚树，可以把树的结点数下降到2m-1以内，从而大大提高树形DP的效率。

代码实现：

 

  1 #include<stdio.h>
  2 #include<string.h>
  3 #include<algorithm>
  4 #include<queue>
  5 #include<vector>
  6 #include<stack>
  7 using namespace std;
  8 const int MAXN=100006;
  9 /**
 10 @var d[v]    结点v的深度
 11 @var f[v][i] 结点v的第2^i个祖先
 12 @var id[v]   结点的dfs序
 13 @var e[v]    结点v在原树邻接表
 14 @var vt[v]   结点v在虚树上包含的邻接表
 15 @var que     要查询的结点的集合（虚树必须包含的结点）
 16 @var LN      log2(最大深度)的向下取值
 17 @var st      栈，用于构建ST表
 18 @var z       dfs序的计数器
 19 注意结点标号必须从1开始，因为0拿去当空结点了。
 20 */
 21 int d[MAXN],f[MAXN][18],id[MAXN],LN=0,z,st[MAXN];
 22 vector<int>e[MAXN],vt[MAXN],que;
 23 int init(int n)
 24 {
 25     z=0;
 26     memset(f,0,sizeof(f));
 27     for(int i=1; i<=n; i++)
 28         e[i].clear();
 29     d[0]=-1;
 30     LN=0;
 31 }
 32 void dfs(int v,int deep)
 33 {
 34     d[v]=deep;
 35     st[deep]=v;
 36     id[v]=++z;
 37     if((1<<LN)<deep)
 38         LN++;
 39     int i,j;
 40     for(i=1,j=0; i<=deep; i<<=1,j++)
 41     {
 42         f[v][j]=st[deep-i];
 43     }
 44     for(i=0; i<e[v].size(); i++)
 45     {
 46         if(e[v][i]!=f[v][0])
 47         {
 48             dfs(e[v][i],deep+1);
 49         }
 50     }
 51 }
 52 int lca(int x,int y)
 53 {
 54     if(d[x]<d[y])
 55         swap(x,y);
 56     int i;
 57     for(i=LN; i>=0; i--)
 58     {
 59         if(f[x][i]&&d[f[x][i]]>=d[y])
 60             x=f[x][i];
 61     }
 62     if(x==y)
 63         return x;
 64     for(i=LN; i>=0; i--)
 65     {
 66         if(f[x][i]>0&&f[x][i]!=f[y][i])
 67         {
 68             x=f[x][i];
 69             y=f[y][i];
 70         }
 71     }
 72     return f[x][0];
 73 }
 74 int cmp(const int &x,const int &y)
 75 {
 76     return id[x]<id[y];
 77 }
 78 int build(vector<int> &que)
 79 {
 80     int i,j,k,temp;
 81     sort(que.begin(),que.end(),cmp);
 82     stack<int>st;
 83     st.push(que[0]);
 84     vt[que[0]].clear();
 85     for(i=1; i<que.size(); i++)///每次有出栈的时候开始建边
 86     {
 87         k=lca(que[i],st.top());
 88         temp=0;
 89         while(!st.empty()&&lca(k,st.top())!=st.top())
 90         {
 91             if(temp)
 92                 vt[st.top()].push_back(temp);
 93             temp=st.top();
 94             st.pop();
 95         }
 96         if(st.empty()||st.top()!=k)
 97         {
 98             st.push(k);
 99             vt[k].clear();
100         }
101         if(temp)
102             vt[st.top()].push_back(temp);
103         st.push(que[i]);
104         vt[que[i]].clear();
105     }
106     temp=0;
107     while(!st.empty())
108     {
109         if(temp)
110             vt[st.top()].push_back(temp);
111         temp=st.top();
112         st.pop();
113     }
114     return temp;
115 }
虚树

 习题：http://codeforces.com/problemset/problem/613/D

这题需要树形DP基础，而且要讨论的情况有点多，所以其实有点不适合入门.....，因为很可能被树形DP卡住

posted @ 2018-04-01 12:41  强势围观  阅读(1451)  评论(0)  编辑  收藏  举报