2016.10.14【周赛】第二周周赛——打怪升级不按套路 ——题解
A:
A题很简单只要满足两个条件即可
1.abs(a)+abs(b)<=s
2.s-abs(a)-abs(b)是偶数
附AC代码
1 #include<stdio.h> 2 int main() 3 { 4 int a,b,s; 5 scanf("%d%d%d",&a,&b,&s); 6 if(a<0) 7 a=-a; 8 if(b<0) 9 b=-b; 10 if(a+b<=s&&(s-a-b)%2==0) 11 puts("Yes"); 12 else 13 puts("No"); 14 15 return 0; 16 }
B:
这题是道简单的贪心,只要排序一下,再从大到小拿走即可,因为数据很小,也可以两个for暴力
附AC代码
1 #include<stdio.h> 2 #include<algorithm> 3 using namespace std; 4 int main() 5 { 6 int n,i,a[105],sum=0,s=0; 7 scanf("%d",&n); 8 for(i=0;i<n;i++) 9 { 10 scanf("%d",&a[i]); 11 sum+=a[i]; 12 } 13 sort(a,a+n); 14 for(i=1;i<=n;i++) 15 { 16 s+=a[n-i]; 17 if(s+s>sum) 18 break; 19 } 20 printf("%d\n",i); 21 return 0; 22 }
C:这题是道简单的dp,难点在于转化模型
这是其实不难发现这题就是简单台阶模型,我们可以这样看
假设 你目前位于0的位置,然后你一步最大可以跨过m级台阶,这时你两步间留下的没被踩到的阶梯的个数刚好小于m,这和题目要求的模型一模一样。
不难得出转移方程 dp[i]=dp[i-1]+dp[i-2]+……+dp[i-m] ,然后就是上界的问题,由于第n个位置可以种或不种,即第n阶台阶可以跨过去,所以上界应选n+1。最后再注意一下int会溢出,应该使用long long就能AC了
附AC代码
1 #include<stdio.h> 2 #include<string.h> 3 int main() 4 { 5 int i,j,n,m; 6 long long dp[100]; 7 while(scanf("%d%d",&n,&m)!=EOF) 8 { 9 10 memset(dp,0,sizeof(dp)); 11 dp[0]=1; 12 for(i=0;i<=n;i++) 13 { 14 for(j=1;j<=m;j++) 15 dp[i+j]+=dp[i]; 16 } 17 printf("%I64d\n",dp[n+1]); 18 } 19 return 0; 20 }
D:
这题是道简单的模拟题,唯一的难点是判断是否能追上,首先我们不难得出地图里路径走到最后一定是形成了各自的循环,考虑到地图的大小我们可以推测猫和老鼠各自的周期肯定小于100,如果他们能相遇的话,时间一定不可能大于公共最小周期,所以设个时间限制100*100,超过这个时间就肯定追不到了(你设得大一点也行,因为时间限制很宽裕,事实上这个值可以设得比10000还小得多)
附AC代码
1 #include<stdio.h> 2 #include<string.h> 3 char Map[15][15]; 4 struct Pos 5 { 6 int dir; 7 int x,y; 8 9 } mouse,cat; 10 11 Pos move(Pos animal) 12 { 13 int x=animal.x,y=animal.y,dir=animal.dir; 14 if(dir==0&&Map[x-1][y]) 15 { 16 animal.x--; 17 } 18 else if(dir==1&&Map[x][y+1]) 19 { 20 animal.y++; 21 } 22 else if(dir==2&&Map[x+1][y]) 23 { 24 animal.x++; 25 } 26 else if(dir==3&&Map[x][y-1]) 27 { 28 animal.y--; 29 } 30 else 31 { 32 animal.dir++; 33 } 34 return animal; 35 } 36 37 int main() 38 { 39 int n,i,j,t,time; 40 char s[15]; 41 scanf("%d",&t); 42 while(t--) 43 { 44 memset(Map,0,sizeof(Map)); 45 mouse.dir=0; 46 cat.dir=0; 47 time=0; 48 for(i=1; i<=10; i++) 49 { 50 scanf("%s",&s); 51 for(j=1; j<=10; j++) 52 { 53 Map[i][j]=(s[j-1]!='*'); 54 if(s[j-1]=='m') 55 { 56 mouse.x=i; 57 mouse.y=j; 58 59 } 60 else if(s[j-1]=='c') 61 { 62 cat.x=i; 63 cat.y=j; 64 } 65 } 66 } 67 while(1) 68 { 69 mouse.dir%=4; 70 cat.dir%=4; 71 mouse=move(mouse); 72 cat=move(cat); 73 time++; 74 if(time>10000) 75 { 76 printf("0\n"); 77 break; 78 } 79 if(mouse.x==cat.x&&mouse.y==cat.y) 80 { 81 printf("%d\n",time); 82 break; 83 } 84 } 85 } 86 return(0); 87 }
E:这题作为压轴大题,复杂度,和难度相比之前的题都有着爆炸式增长,前面之所以有那么多水题,是希望能留够时间给大家做这道题。由于这题数据较大,大家做矩阵乘法法时一定要小心long long的溢出,我写的矩阵乘法是加完再MOD,结果做加法时溢出,导致WA一次。
这题就不附完整的AC代码了,而是给出思路,和部分代码,希望读者能独立的做出来这道超级模板题。
首先先看提示

从中不难看出杨辉三角的影子
其实矩阵是这样构造的
首先构造齐K次递推方程组 即
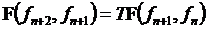

然后将方程转化成矩阵

设

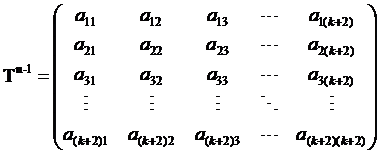
显然有

1 #include<stdio.h> 2 #include<string.h> 3 struct matrix 4 { 5 long long m[60][60];/** m的类型注意调整*/ 6 }e,o; 7 long long c[100][100]; 8 9 int main() 10 { 11 12 int i,n,k,j,m,x,l,f1,f2,a,b,t; 13 long long v[60],temp; 14 matrix T; 15 memset(e.m,0,sizeof(e.m)); 16 for(i=0;i<52;i++) 17 e.m[i][i]=1;/**初始化单位阵*/ 18 memset(o.m,0,sizeof(o.m));/**初始化零矩阵*/ 19 c[0][0]=1; 20 for(i=1;i<=52;i++) 21 { 22 c[i][0]=1; 23 for(j=1;j<=i;j++) 24 c[i][j]=c[i-1][j-1]+c[i-1][j]; 25 } 26 scanf("%d",&t); 27 while(t--) 28 { 29 scanf("%d%d%d%d%d%d%d",&f1,&f2,&a,&b,&k,&n,&m); 30 memset(T.m,0,sizeof(T.m)); 31 T.m[k][0]=1; 32 for(i=k-1;i>=0;i--) 33 { 34 for(j=0;j<k-i;j++) 35 { 36 T.m[i][j]=T.m[i+1][j]*a%m; 37 } 38 T.m[i][k-i]=T.m[i+1][k-i-1]*b%m; 39 } 40 for(i=0;i<k;i++) 41 { 42 for(j=0;j<=k-i;j++) 43 { 44 T.m[i][j]=T.m[i][j]*(c[k-i][j]%m)%m; 45 } 46 } 47 T.m[k+1][0]=1; 48 T.m[k+1][k+1]=1; 49 for(i=0;i<=k+1;i++) 50 { 51 for(j=0;j<=k+1;j++) 52 printf("%5I64d",T.m[i][j]); 53 puts(""); 54 } 55 v[0]=1,temp=1; 56 for(i=1;i<=k;i++) 57 { 58 v[i]=v[i-1]*f1%m; 59 } 60 for(i=k-1;i>=0;i--) 61 { 62 temp=temp*f2%m; 63 v[i]=v[i]*temp%m; 64 } 65 v[k+1]=v[k]; 66 matpow(T,n-1,k+2,m,v); 67 } 68 return 0; 69 }




