实验三:朴素贝叶斯算法实验
【实验目的】
理解朴素贝叶斯算法原理,掌握朴素贝叶斯算法框架。
【实验内容】
针对下表中的数据,编写python程序实现朴素贝叶斯算法(不使用sklearn包),对输入数据进行预测;
熟悉sklearn库中的朴素贝叶斯算法,使用sklearn包编写朴素贝叶斯算法程序,对输入数据进行预测;
【实验报告要求】
对照实验内容,撰写实验过程、算法及测试结果;
代码规范化:命名规则、注释;
查阅文献,讨论朴素贝叶斯算法的应用场景。
| 色泽 | 根蒂 | 敲声 | 纹理 | 脐部 | 触感 | 好瓜 |
| 青绿 | 蜷缩 | 浊响 | 清晰 | 凹陷 | 碍滑 | 是 |
| 乌黑 | 蜷缩 | 沉闷 | 清晰 | 凹陷 | 碍滑 | 是 |
| 乌黑 | 蜷缩 | 浊响 | 清晰 | 凹陷 | 碍滑 | 是 |
| 青绿 | 蜷缩 | 沉闷 | 清晰 | 凹陷 | 碍滑 | 是 |
| 浅白 | 蜷缩 | 浊响 | 清晰 | 凹陷 | 碍滑 | 是 |
| 青绿 | 稍蜷 | 浊响 | 清晰 | 稍凹 | 软粘 | 是 |
| 乌黑 | 稍蜷 | 浊响 | 稍糊 | 稍凹 | 软粘 | 是 |
| 乌黑 | 稍蜷 | 浊响 | 清晰 | 稍凹 | 硬滑 | 是 |
| 乌黑 | 稍蜷 | 沉闷 | 稍糊 | 稍凹 | 硬滑 | 否 |
| 青绿 | 硬挺 | 清脆 | 清晰 | 平坦 | 软粘 | 否 |
| 浅白 | 硬挺 | 清脆 | 模糊 | 平坦 | 硬滑 | 否 |
| 浅白 | 蜷缩 | 浊响 | 模糊 | 平坦 | 软粘 | 否 |
| 青绿 | 稍蜷 | 浊响 | 稍糊 | 凹陷 | 硬滑 | 否 |
| 浅白 | 稍蜷 | 沉闷 | 稍糊 | 凹陷 | 硬滑 | 否 |
| 乌黑 | 稍蜷 | 浊响 | 清晰 | 稍凹 | 软粘 | 否 |
| 浅白 | 蜷缩 | 浊响 | 模糊 | 平坦 | 硬滑 | 否 |
| 青绿 | 蜷缩 | 沉闷 | 稍糊 | 稍凹 | 硬滑 | 否 |
一、编写python程序实现朴素贝叶斯算法(不使用sklearn包)
#导入包和数据
import numpy as np import pandas as pd data_list = [ ['青绿', '蜷缩', '浊响', '清晰', '凹陷', '碍滑', 'YES'], ['乌黑', '蜷缩', '沉闷', '清晰', '凹陷', '碍滑', 'YES'], ['乌黑', '蜷缩', '浊响', '清晰', '凹陷', '碍滑', 'YES'], ['青绿', '蜷缩', '沉闷', '清晰', '凹陷', '碍滑', 'YES'], ['浅白', '蜷缩', '浊响', '清晰', '凹陷', '碍滑', 'YES'], ['青绿', '稍缩', '浊响', '清晰', '稍凹', '软粘', 'YES'], ['乌黑', '稍缩', '浊响', '清晰', '稍凹', '软粘', 'YES'], ['乌黑', '稍缩', '浊响', '清晰', '稍凹', '硬滑', 'YES'], ['乌黑', '稍缩', '沉闷', '稍糊', '稍凹', '硬滑', 'NO'], ['青绿', '硬挺', '清脆', '清晰', '平坦', '软粘', 'NO'], ['浅白', '硬挺', '清脆', '模糊', '平坦', '硬滑', 'NO'], ['浅白', '蜷缩', '浊响', '模糊', '平坦', '软粘', 'NO'], ['青绿', '稍缩', '浊响', '稍糊', '凹陷', '硬滑', 'NO'], ['浅白', '稍缩', '沉闷', '稍糊', '凹陷', '硬滑', 'NO'], ['乌黑', '稍缩', '浊响', '清晰', '稍凹', '软粘', 'NO'], ['浅白', '蜷缩', '浊响', '模糊', '稍凹', '硬滑', 'NO'], ['青绿', '蜷缩', '沉闷', '稍糊', '稍凹', '硬滑', 'NO'] ] classes_list = ['色泽','根蒂','敲声','纹理','脐部','触感','好瓜'] property_list = [ '青绿','乌黑','浅白', '蜷缩','稍蜷','硬挺', '浊响','沉闷','清脆', '清晰','稍糊','模糊', '凹陷','平坦','稍凹', '硬滑','软粘',]
class NaiveBayes:
def __init__(self):
self.model = {}#key 为类别名 val 为字典PClass表示该类的该类,PFeature:{}对应对于各个特征的概率
# def calEntropy(self, y): # 计算熵
# valRate = y.value_counts().apply(lambda x : x / y.size) # 频次汇总 得到各个特征对应的概率
# valEntropy = np.inner(valRate, np.log2(valRate)) * -1 #矩阵内积相乘
# return valEntropy
def fit(self, xTrain, yTrain = pd.Series()):
if not yTrain.empty:#如果不传,自动选择最后一列作为分类标签
xTrain = pd.concat([xTrain, yTrain], axis=1) #按列合并
self.model = self.buildNaiveBayes(xTrain)
return self.model
def buildNaiveBayes(self, xTrain):
yTrain = xTrain.iloc[:,-1] #获取特征
yTrainCounts = yTrain.value_counts()# 得到各个特征对应的概率
yTrainCounts = yTrainCounts.apply(lambda x : (x + 1) / (yTrain.size + yTrainCounts.size)) #使用了拉普拉斯平滑 分别计算YES和NO的概率
# print("1111:",yTrainCounts)
# print("@@@")
retModel = {} #使用拉普拉斯的模型
for nameClass, val in yTrainCounts.items():
retModel[nameClass] = {'PClass': val, 'PFeature':{}}
# print("@@")
# print(retModel)
# print("@@")
propNamesAll = xTrain.columns[:-1] #训练数据
# print("@@")
# print(xTrain[propNamesAll])
# print("@@")
allPropByFeature = {}
for nameFeature in propNamesAll:
allPropByFeature[nameFeature] = list(xTrain[nameFeature].value_counts().index)#获取每列的特征
# print("@@")
# print(allPropByFeature)
# print("@@")
for nameClass, group in xTrain.groupby(xTrain.columns[-1]): #根据最后一列分组
for nameFeature in propNamesAll:
eachClassPFeature = {}
propDatas = group[nameFeature]
propClassSummary = propDatas.value_counts()# 频次汇总 得到各个特征对应的概率
for propName in allPropByFeature[nameFeature]:
if not propClassSummary.get(propName):
propClassSummary[propName] = 0#如果有属性没有,那么自动补0
Ni = len(allPropByFeature[nameFeature])
propClassSummary = propClassSummary.apply(lambda x : (x + 1) / (propDatas.size + Ni))#使用了拉普拉斯平滑 计算条件概率
for nameFeatureProp, valP in propClassSummary.items():
eachClassPFeature[nameFeatureProp] = valP
retModel[nameClass]['PFeature'][nameFeature] = eachClassPFeature
# print("@@")
# print(propClassSummary)
# print("@@")
return retModel
def predictBySeries(self, data):
curMaxRate = None
curClassSelect = None
for nameClass, infoModel in self.model.items():
rate = 0
rate += np.log(infoModel['PClass'])
PFeature = infoModel['PFeature'] #每个特征的概率
for nameFeature, val in data.items():
propsRate = PFeature.get(nameFeature)
if not propsRate:
continue
rate += np.log(propsRate.get(val, 0))#使用log加法避免很小的小数连续乘,接近零
#print(nameFeature, val, propsRate.get(val, 0))
#print(nameClass, rate)
if curMaxRate == None or rate > curMaxRate:
curMaxRate = rate
curClassSelect = nameClass
# print("@@")
# print(PFeature)
# print("@@")
return curClassSelect
def predict(self, data):
if isinstance(data, pd.Series): #对比类型
return self.predictBySeries(data)
return data.apply(lambda d: self.predictBySeries(d), axis=1)
dataTrain = data
naiveBayes = NaiveBayes()
treeData = naiveBayes.fit(dataTrain)
import json
print(json.dumps(treeData, ensure_ascii=False))
pd = pd.DataFrame({'预测值':naiveBayes.predict(dataTrain), '正取值':dataTrain.iloc[:,-1]})
print(pd)
print('正确率:%f%%'%(pd[pd['预测值'] == pd['正取值']].shape[0] * 100.0 / pd.shape[0]))

二、使用sklearn包编写朴素贝叶斯算法程序
# 输入数据集
datasets1 = [['0', '0', '0', '0', '0', '0', '1'],
['1', '0', '1', '0', '0', '0', '1'],
['1', '0', '0', '0', '0', '0', '1'],
['0', '0', '1', '0', '0', '0', '1'],
['2', '0', '0', '0', '0', '0', '1'],
['0', '1', '0', '0', '1', '1', '1'],
['1', '1', '0', '1', '1', '1', '1'],
['1', '1', '0', '0', '1', '2', '1'],
['1', '1', '1', '1', '1', '2', '0'],
['0', '2', '2', '0', '2', '1', '0'],
['2', '2', '2', '2', '2', '2', '0'],
['2', '0', '0', '2', '2', '1', '0'],
['0', '1', '0', '1', '0', '2', '0'],
['2', '1', '1', '1', '0', '2', '0'],
['1', '1', '0', '0', '1', '1', '0'],
['2', '0', '0', '2', '2', '2', '0'],
['0', '0', '1', '1', '1', '2', '0']
]
# 青绿:0 乌黑:1 浅白:2
# 蜷缩 0 稍蜷 1 硬挺 2
# 浊响 0 沉闷 1 清脆 2
# 清晰 0 稍糊 1 模糊 2
# 凹陷 0 稍凹 1 平坦 2
# 碍滑 0 软粘 1 硬滑 2
# 是 1 否 0
labels = ['色泽', '根蒂', '敲声', '纹理', '脐部', '触感', '好瓜']
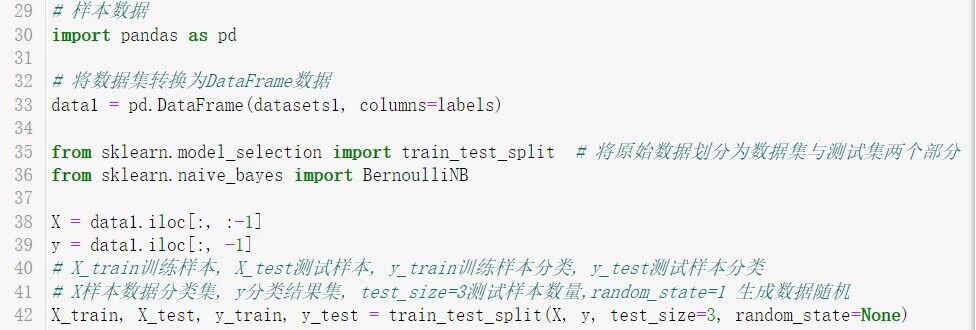
# 样本数据
import pandas as pd
# 将数据集转换为DataFrame数据
data1 = pd.DataFrame(datasets1, columns=labels)
from sklearn.model_selection import train_test_split # 将原始数据划分为数据集与测试集两个部分
from sklearn.naive_bayes import BernoulliNB
X = data1.iloc[:, :-1]
y = data1.iloc[:, -1]
# X_train训练样本, X_test测试样本, y_train训练样本分类, y_test测试样本分类
# X样本数据分类集, y分类结果集, test_size=3测试样本数量,random_state=1 生成数据随机
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=3, random_state=None)
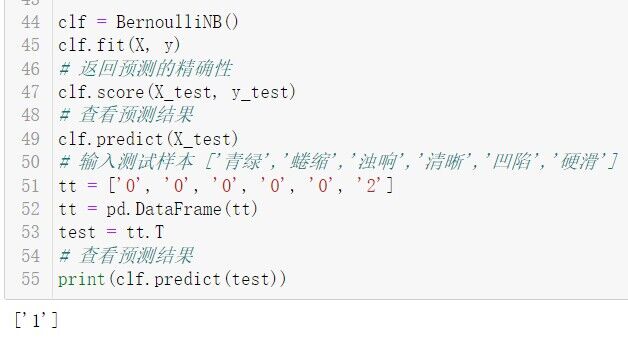
clf = BernoulliNB()
clf.fit(X, y)
# 返回预测的精确性
clf.score(X_test, y_test)
# 查看预测结果
clf.predict(X_test)
# 输入测试样本 ['青绿','蜷缩','浊响','清晰','凹陷','硬滑']
tt = ['0', '0', '0', '0', '0', '2']
tt = pd.DataFrame(tt)
test = tt.T
# 查看预测结果
print(clf.predict(test))