决策树算法实验
决策树算法实验
【实验目的】
1、理解决策树算法原理,掌握决策树算法框架;
2、理解决策树学习算法的特征选择、树的生成和树的剪枝;
3、能根据不同的数据类型,选择不同的决策树算法;
4、针对特定应用场景及数据,能应用决策树算法解决实际问题。
【实验内容】
1、设计算法实现熵、经验条件熵、信息增益等方法。
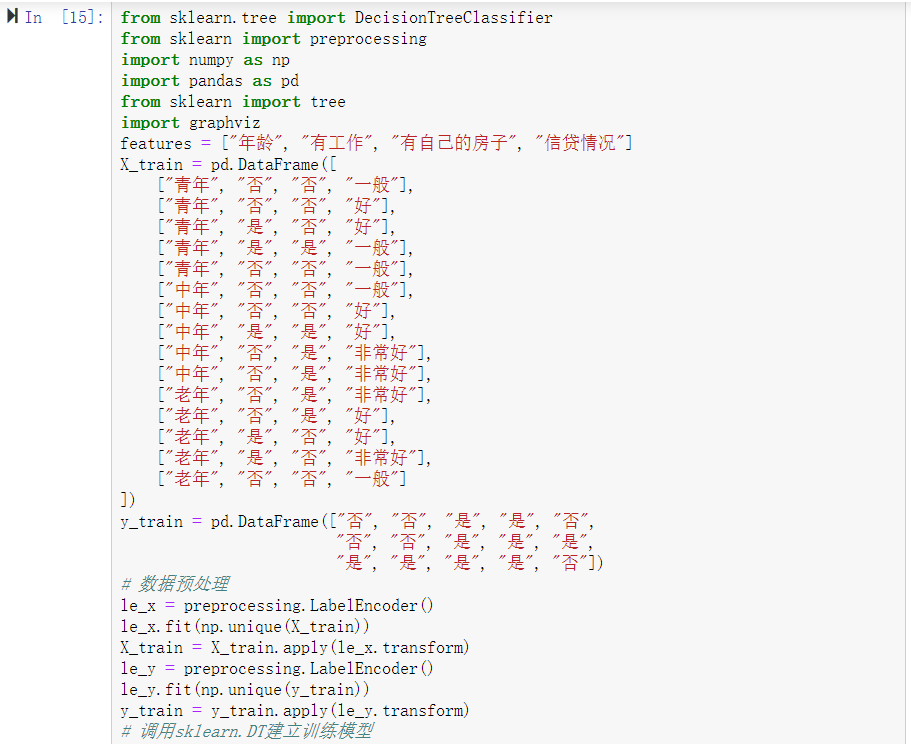
2、针对给定的房贷数据集(数据集表格见附录1)实现ID3算法。
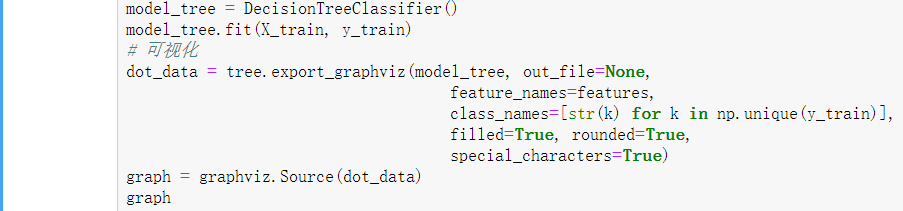
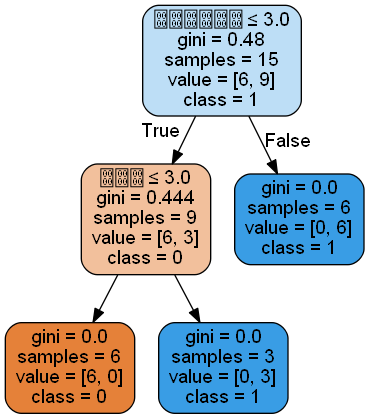
3、熟悉sklearn库中的决策树算法;
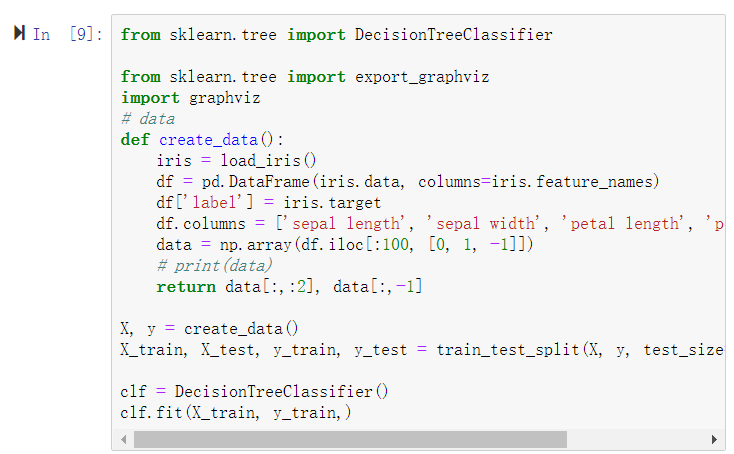
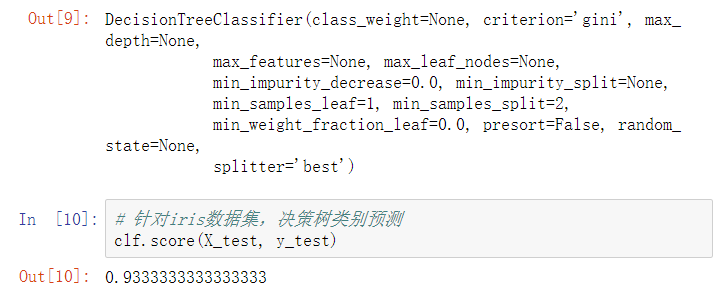
4、针对iris数据集,应用sklearn的决策树算法进行类别预测。
【实验报告要求】
1、对照实验内容,撰写实验过程、算法及测试结果;
2、代码规范化:命名规则、注释;
3、查阅文献,讨论ID3、5算法的应用场景;
实验过程
1、导包

2、导入数据集

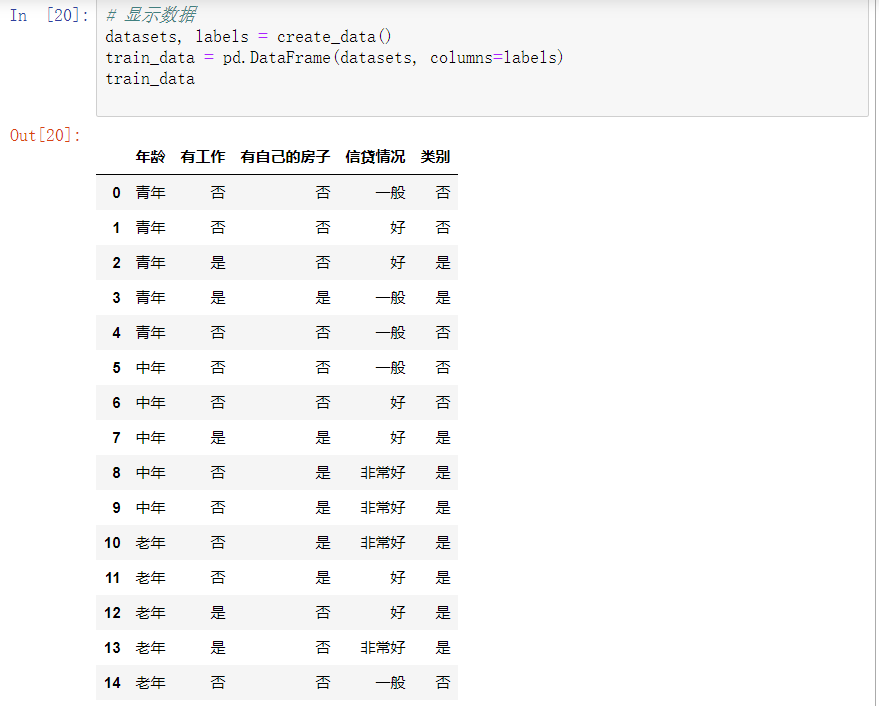
3、转为DataFrame显示数据集
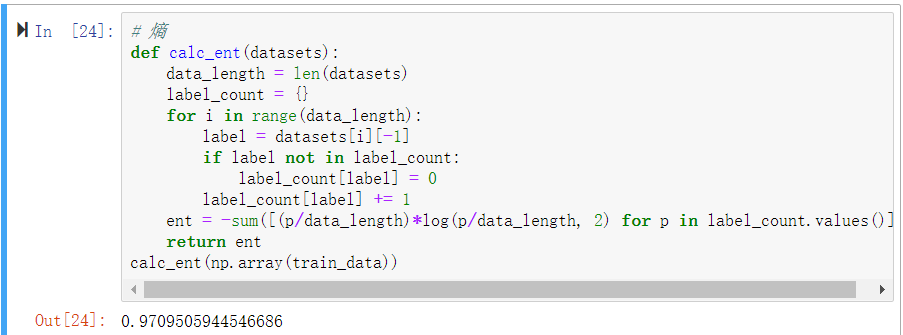
4、计算熵
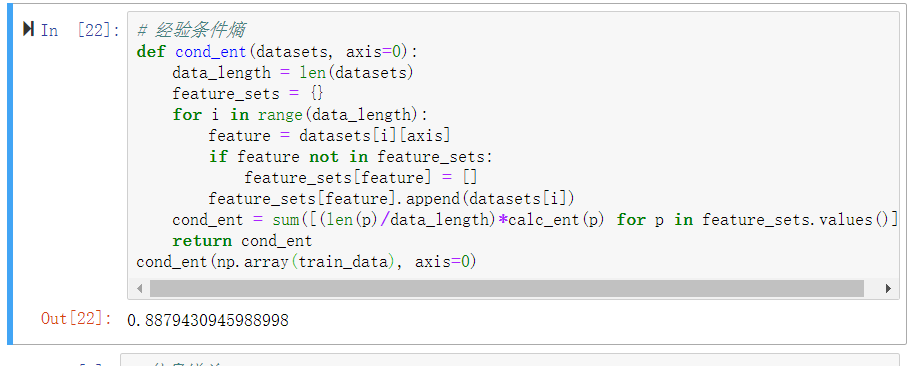
5、计算经验条件熵
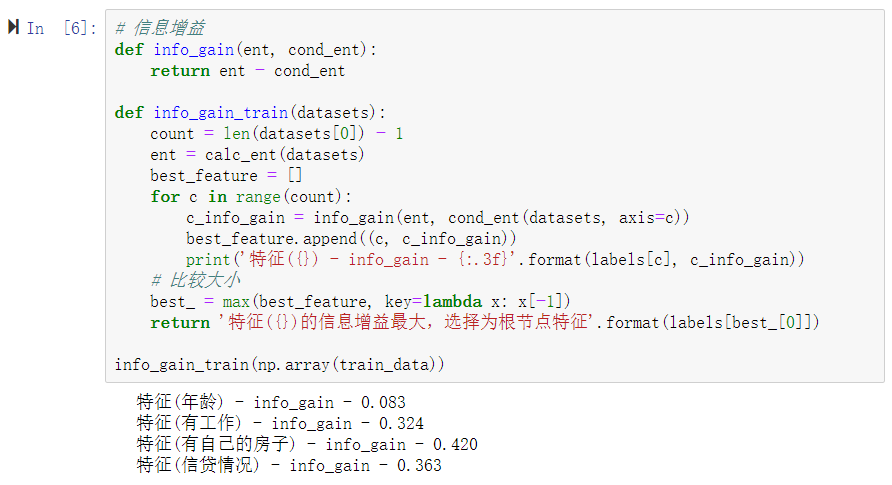
6、计算信息增益
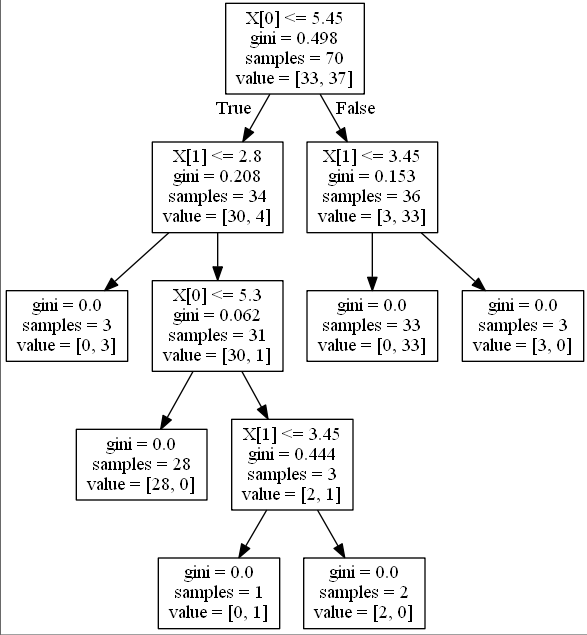
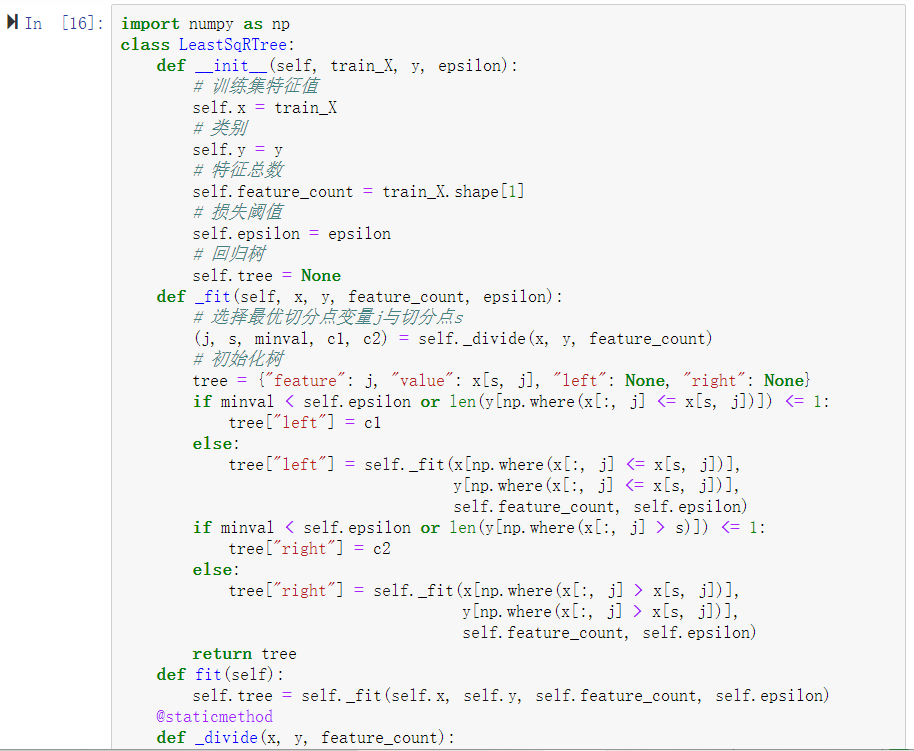
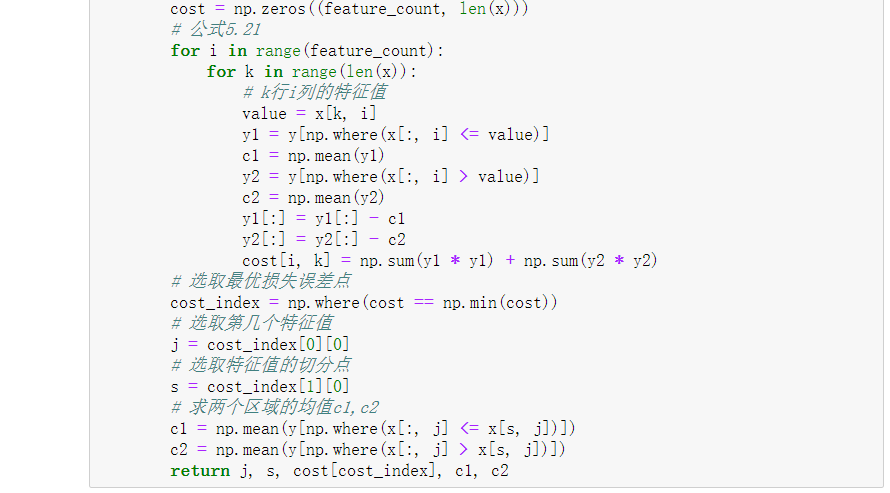
7、利用ID3算法生成决策树
'''利用ID3算法生成决策树'''
# 定义节点类 二叉树
class Node:
def __init__(self, root=True, label=None, feature_name=None, feature=None):
self.root = root
self.label = label
self.feature_name = feature_name
self.feature = feature
self.tree = {}
self.result = {'label:': self.label, 'feature': self.feature, 'tree': self.tree}
def __repr__(self):
return '{}'.format(self.result)
def add_node(self, val, node):
self.tree[val] = node
def predict(self, features):
if self.root is True:
return self.label
return self.tree[features[self.feature]].predict(features)
class DTree:
def __init__(self, epsilon=0.1):
self.epsilon = epsilon
self._tree = {}
# 熵
@staticmethod
def calc_ent(datasets):
data_length = len(datasets)
label_count = {}
for i in range(data_length):
label = datasets[i][-1]
if label not in label_count:
label_count[label] = 0
label_count[label] += 1
ent = -sum([(p/data_length)*log(p/data_length, 2) for p in label_count.values()])
return ent
# 经验条件熵
def cond_ent(self, datasets, axis=0):
data_length = len(datasets)
feature_sets = {}
for i in range(data_length):
feature = datasets[i][axis]
if feature not in feature_sets:
feature_sets[feature] = []
feature_sets[feature].append(datasets[i])
cond_ent = sum([(len(p)/data_length)*self.calc_ent(p) for p in feature_sets.values()])
return cond_ent
# 信息增益
@staticmethod
def info_gain(ent, cond_ent):
return ent - cond_ent
def info_gain_train(self, datasets):
count = len(datasets[0]) - 1
ent = self.calc_ent(datasets)
best_feature = []
for c in range(count):
c_info_gain = self.info_gain(ent, self.cond_ent(datasets, axis=c))
best_feature.append((c, c_info_gain))
# 比较大小
best_ = max(best_feature, key=lambda x: x[-1])
return best_
def train(self, train_data):
"""
input:数据集D(DataFrame格式),特征集A,阈值eta
output:决策树T
"""
_, y_train, features = train_data.iloc[:, :-1], train_data.iloc[:, -1], train_data.columns[:-1]
# 1,若D中实例属于同一类Ck,则T为单节点树,并将类Ck作为结点的类标记,返回T
if len(y_train.value_counts()) == 1:
return Node(root=True,
label=y_train.iloc[0])
# 2, 若A为空,则T为单节点树,将D中实例树最大的类Ck作为该节点的类标记,返回T
if len(features) == 0:
return Node(root=True, label=y_train.value_counts().sort_values(ascending=False).index[0])
# 3,计算最大信息增益 同5.1,Ag为信息增益最大的特征
max_feature, max_info_gain = self.info_gain_train(np.array(train_data))
max_feature_name = features[max_feature]
# 4,Ag的信息增益小于阈值eta,则置T为单节点树,并将D中是实例数最大的类Ck作为该节点的类标记,返回T
if max_info_gain < self.epsilon:
return Node(root=True, label=y_train.value_counts().sort_values(ascending=False).index[0])
# 5,构建Ag子集
node_tree = Node(root=False, feature_name=max_feature_name, feature=max_feature)
feature_list = train_data[max_feature_name].value_counts().index
for f in feature_list:
sub_train_df = train_data.loc[train_data[max_feature_name] == f].drop([max_feature_name], axis=1)
# 6, 递归生成树
sub_tree = self.train(sub_train_df)
node_tree.add_node(f, sub_tree)
# pprint.pprint(node_tree.tree)
return node_tree
def fit(self, train_data):
self._tree = self.train(train_data)
return self._tree
def predict(self, X_test):
return self._tree.predict(X_test)
datasets, labels = create_data()
data_df = pd.DataFrame(datasets, columns=labels)
dt = DTree()
tree = dt.fit(data_df)
tree



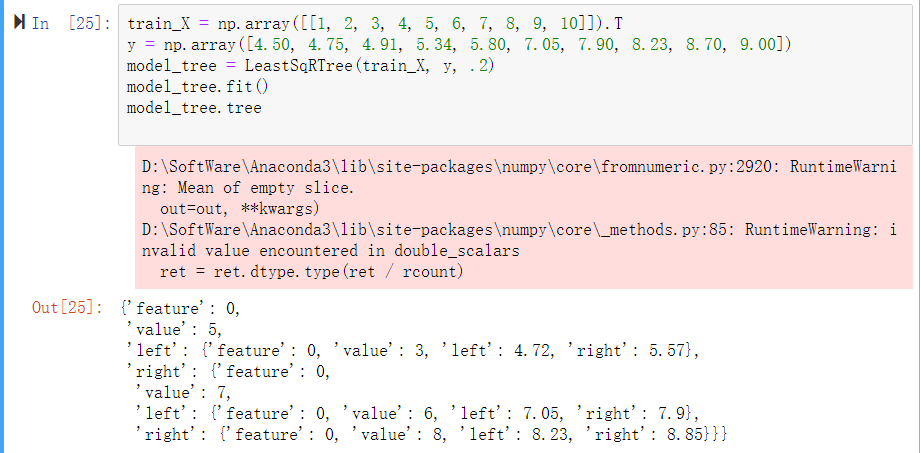
实验小结:
讨论ID3算法的应用场景
ID3算法应用场景:
通过本次实验,我对决策树算法实验和ID3算法有了更近一步的掌握,ID3 使用的分类标准是信息增益,它表示得知特征 A 的信息而使得样本集合不确定性减少的程度。ID3 没有剪枝策略,容易过拟合;信息增益准则对可取值数目较多的特征有所偏好,类似“编号”的特征其信息增益接近于 1;只能用于处理离散分布的特征;没有考虑缺失值。C4.5 引入悲观剪枝策略进行后剪枝;引入信息增益率作为划分标准;将连续特征离散化,假设 n 个样本的连续特征 A 有 m 个取值,C4.5 将其排序并取相邻两样本值的平均数共 m-1 个划分点,分别计算以该划分点作为二元分类点时的信息增益,并选择信息增益最大的点作为该连续特征的二元离散分类点;信息增益率对可取值较少的特征有所偏好(分母越小,整体越大),因此 C4.5 并不是直接用增益率最大的特征进行划分,而是使用一个启发式方法:先从候选划分特征中找到信息增益高于平均值的特征,再从中选择增益率最高的。
决策树剪枝策略分析:
先对数据集划分成训练集和验证集,训练集用来决定书生成过程中每个节点划分选择的属性,验证集在预剪枝中用于决定该节点是否有必要一句改属性进行展开,在后剪枝中用于判断该节点是否需要进行剪枝。先剪枝(pruning)的目的是为了避免决策树模型的过拟合。因为决策树算法在学习的过程中为了尽可能的正确的分类训练样本,不停地对结点进行划分,因此这会导致整棵树的分支过多,也就导致了过拟合。决策树的剪枝策略最基本的有两种:预剪枝(pre-pruning)和后剪枝(post-pruning),预剪枝就是在构造决策树的过程中,先对每个结点在划分前进行估计,若果当前结点的划分不能带来决策树模型泛华性能的提升,则不对当前结点进行划分并且将当前结点标记为叶结点。



