Codeforces Round #333 (Div. 1) C. Kleofáš and the n-thlon 树状数组优化dp

C. Kleofáš and the n-thlon

Time Limit: 20 Sec

Memory Limit: 256 MB

题目连接

http://codeforces.com/contest/601/problem/C

Description

Kleofáš is participating in an n-thlon - a tournament consisting of n different competitions in n different disciplines (numbered 1 throughn). There are m participants in the n-thlon and each of them participates in all competitions.

In each of these n competitions, the participants are given ranks from 1 to m in such a way that no two participants are given the same rank - in other words, the ranks in each competition form a permutation of numbers from 1 to m. The score of a participant in a competition is equal to his/her rank in it.

The overall score of each participant is computed as the sum of that participant's scores in all competitions.

The overall rank of each participant is equal to 1 + k, where k is the number of participants with strictly smaller overall score.

The n-thlon is over now, but the results haven't been published yet. Kleofáš still remembers his ranks in each particular competition; however, he doesn't remember anything about how well the other participants did. Therefore, Kleofáš would like to know his expected overall rank.

All competitors are equally good at each discipline, so all rankings (permutations of ranks of everyone except Kleofáš) in each competition are equiprobable.

Input

The first line of the input contains two space-separated integers n (1 ≤ n ≤ 100) and m (1 ≤ m ≤ 1000) — the number of competitions and the number of participants respectively.

Then, n lines follow. The i-th of them contains one integer xi (1 ≤ xi ≤ m) — the rank of Kleofáš in the i-th competition.

Output

Output a single real number – the expected overall rank of Kleofáš. Your answer will be considered correct if its relative or absolute error doesn't exceed 10 - 9.

Namely: let's assume that your answer is a, and the answer of the jury is b. The checker program will consider your answer correct, if .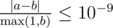

Sample Input

4 10
2
1
2
1

Sample Output

1.0000000000000000

HINT

 

题意

有n场比赛，每场比赛有m个人参加，每场比赛都会排名次

比赛比完了，但是这个人只知道自己每场比赛的名次，并不知道其他人怎么样

于是让你求出这个人排名的期望值

题解：

期望减一后即为所有方案中得分少于主角的人数之和除去总的方案数，换个角度发现这相当于统计一个人得分少于主角的概率再乘以人数，于是dp[i][j]表示前i项比完后得分为j的概率，维护一下区间和可以优化到O(n^2*m)。

 

啊，我比较蠢，所以就直接用树状数组来优化了。。。

代码：

#include<iostream>
#include<stdio.h>
#include<cstring>
using namespace std;

int a[105];
double dp[2][105*1005];
int d[2][105*1005];
struct Bit
{
    double a[105*1005];
    int lowbit(int x)
    {
        return x&(-x);
    }
    double query(int x)
    {
        x++;
        if(x<=0)return 0;
        double ans = 0;
        for(;x;x-=lowbit(x))
            ans+=a[x];
        return ans;
    }
    void updata(int x,double v)
    {
        x++;
        if(x<=0)return;
        for(;x<105*1005;x+=lowbit(x))
            a[x]+=v;
    }
}T[2];
int main()
{
    int n,m;
    scanf("%d%d",&n,&m);
    int sum = 0;
    for(int i=1;i<=n;i++)
    {
        scanf("%d",&a[i]);
        sum+=a[i];
    }
    a[0]=99999;
    if(m==1)
        return puts("1.00000000000000");
    int now = 1;
    dp[now][0]=1;
    T[now].updata(0,1.0);
    for(int i=1;i<=n;i++)
    {
        now = now ^ 1;
        memset(dp[now],0,sizeof(dp[now]));
        memset(T[now].a,0,sizeof(T[now].a));
        for(int j=1;j<=n*m;j++)
        {
            double K = (T[now^1].query(j-1) - T[now^1].query(j-m-1));
            if(j-a[i]>=0)K-=dp[now^1][j-a[i]];
            K*=1.0/(m-1.0);
            dp[now][j] += K;
            T[now].updata(j,dp[now][j]);
        }
    }
    double res = 0;
    for(int i=0;i<sum;i++)
        res+=dp[now][i];
    printf("%.15f\n",res*(m-1)+1.0);
}