Codeforces Round #333 (Div. 1) B. Lipshitz Sequence 倍增 二分

B. Lipshitz Sequence

Time Limit: 20 Sec

Memory Limit: 256 MB

题目连接

http://codeforces.com/contest/601/problem/B

Description

A function 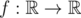 is called Lipschitz continuous if there is a real constant K such that the inequality |f(x) - f(y)| ≤ K·|x - y| holds for all 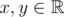. We'll deal with a more... discrete version of this term.

For an array 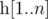, we define it's Lipschitz constant  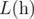as follows:

• if n < 2, 
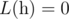
• if n ≥ 2, 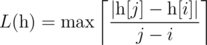 over all 1 ≤ i < j ≤ n

In other words, 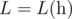 is the smallest non-negative integer such that |h[i] - h[j]| ≤ L·|i - j| holds for all 1 ≤ i, j ≤ n.

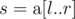You are given an array  of size n and q queries of the form [l, r]. For each query, consider the subarray ; determine the sum of Lipschitz constants of all subarrays of .

Input

The first line of the input contains two space-separated integers n and q (2 ≤ n ≤ 100 000 and 1 ≤ q ≤ 100) — the number of elements in array  and the number of queries respectively.

The second line contains n space-separated integers  ().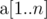

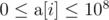The following q lines describe queries. The i-th of those lines contains two space-separated integers li and ri (1 ≤ li < ri ≤ n).

Output

Print the answers to all queries in the order in which they are given in the input. For the i-th query, print one line containing a single integer — the sum of Lipschitz constants of all subarrays of .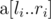

Sample Input

10 4
1 5 2 9 1 3 4 2 1 7
2 4
3 8
7 10
1 9

Sample Output

17
82
23
210

HINT

 

题意

给你n个数，Q次询问，问你区间l,r区间里面的 区间斜率最大值 的区间和 是多少

题解：

比较绕。。。

首先斜率最大值一定是相邻的，这个可以很容易通过画图来解决

然后我们就用st表+二分来找到第一个比他大的数在哪儿就好了~

然后就可以跑一遍就行了

代码：

#include<iostream>
#include<stdio.h>
#include<algorithm>
using namespace std;
#define maxn 100005
int n;
int dp[maxn][20];
int dp1[maxn][20];
int A[maxn];
int a[maxn];
int L[maxn],R[maxn];
int mm[maxn];
void initrmp(int n)
{
    mm[0]=-1;
    for(int i=1;i<=n;i++)
    {
        mm[i]=((i&(i-1))==0)?mm[i-1]+1:mm[i-1];
        dp[i][0]=a[i];
        dp1[i][0]=a[i];
    }
    for(int j = 1;j<=mm[n];j++)
        for(int i=1;i+(1<<j)-1<=n;i++)
            dp[i][j]=max(dp[i][j-1],dp[i+(1<<(j-1))][j-1]);
    for(int j = 1;j<=mm[n];j++)
        for(int i=1;i+(1<<j)-1<=n;i++)
            dp1[i][j]=min(dp1[i][j-1],dp1[i+(1<<(j-1))][j-1]);
}
int queryMax(int l,int r)
{
    int k = mm[r-l+1];
    return max(dp[l][k],dp[r-(1<<k)+1][k]);
}
int queryMin(int l,int r)
{
    int k = mm[r-l+1];
    return min(dp1[l][k],dp1[r-(1<<k)+1][k]);
}
int main()
{
    scanf("%d",&n);
    int q;scanf("%d",&q);
    for(int i=1;i<=n;i++)
        scanf("%d",&A[i]);
    n--;
    for(int i=1;i<=n;i++)
        a[i]=abs(A[i+1]-A[i]);
    int Ans = 0;
    initrmp(n);
    for(int i=1;i<=n;i++)
    {
        int l=1,r=i;
        while(l<=r)
        {
            int mid = (l+r)/2;
            if(queryMax(mid,i-1)<a[i])r=mid-1;
            else l=mid+1;
        }
        L[i]=l;
        l=i,r=n;
        while(l<=r)
        {
            int mid = (l+r)/2;
            if(queryMax(i+1,mid)<=a[i])l=mid+1;
            else r=mid-1;
        }
        R[i]=l-1;
    }

    for(int i=1;i<=q;i++)
    {
        int x,y;scanf("%d%d",&x,&y);
        y--;
        long long Ans = 0;
        for(int j=x;j<=y;j++)
            Ans += 1LL*(j-max(L[j],x)+1)*(min(R[j],y)-j+1)*a[j];
        printf("%lld\n",Ans);
    }
}