Codeforces Round #185 (Div. 2) C. The Closest Pair 构造

C. The Closest Pair

Time Limit: 20 Sec

Memory Limit: 256 MB

题目连接

http://codeforces.com/contest/312/problem/C

Description

Currently Tiny is learning Computational Geometry. When trying to solve a problem called "The Closest Pair Of Points In The Plane", he found that a code which gave a wrong time complexity got Accepted instead of Time Limit Exceeded.

The problem is the follows. Given n points in the plane, find a pair of points between which the distance is minimized. Distance between(x1, y1) and (x2, y2) is .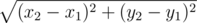

The pseudo code of the unexpected code is as follows:

input n
for i from 1 to n
    input the i-th point's coordinates into p[i]
sort array p[] by increasing of x coordinate first and increasing of y coordinate second
d=INF        //here INF is a number big enough
tot=0
for i from 1 to n
    for j from (i+1) to n
        ++tot
        if (p[j].x-p[i].x>=d) then break    //notice that "break" is only to be
                                            //out of the loop "for j"
        d=min(d,distance(p[i],p[j]))
output d

Here, tot can be regarded as the running time of the code. Due to the fact that a computer can only run a limited number of operations per second, tot should not be more than k in order not to get Time Limit Exceeded.

You are a great hacker. Would you please help Tiny generate a test data and let the code get Time Limit Exceeded?

Input

A single line which contains two space-separated integers n and k (2 ≤ n ≤ 2000, 1 ≤ k ≤ 109).

Output

If there doesn't exist such a data which let the given code get TLE, print "no solution" (without quotes); else print n lines, and the i-th line contains two integers xi, yi (|xi|, |yi| ≤ 109) representing the coordinates of the i-th point.

The conditions below must be held:

• All the points must be distinct.
• |xi|, |yi| ≤ 109.
• After running the given code, the value of tot should be larger than k.

Sample Input

4 3

Sample Output

0 0
0 1
1 0
1 1

HINT

 

题意

给你一个程序，要求让你出一组数据，使得这组数据会让程序的tot超过k

题解：

很显然我们可以发现，他只是比较了x之间的距离，那么我们可以构造出所有点的x都相同，y都不相同的数据就好了

这样任意两个点的距离一定是大于任意两个点的x坐标之差的

代码：

#include<iostream>
#include<stdio.h>
#include<math.h>
using namespace std;

int main()
{
    long long n,k;
    cin>>n>>k;
    if(k>=((n*(n-1LL))/2LL))
        return puts("no solution");
    for(int i=0;i<n;i++)
        printf("1 %d\n",i);
}