Codeforces Round #331 (Div. 2) D. Wilbur and Trees 记忆化搜索

D. Wilbur and Trees

Time Limit: 20 Sec

Memory Limit: 256 MB

题目连接

http://codeforces.com/contest/596/problem/D

Description

Wilbur the pig really wants to be a beaver, so he decided today to pretend he is a beaver and bite at trees to cut them down.

There are n trees located at various positions on a line. Tree i is located at position xi. All the given positions of the trees are distinct.

The trees are equal, i.e. each tree has height h. Due to the wind, when a tree is cut down, it either falls left with probability p, or falls right with probability 1 - p. If a tree hits another tree while falling, that tree will fall in the same direction as the tree that hit it. A tree can hit another tree only if the distance between them is strictly less than h.

For example, imagine there are 4 trees located at positions 1, 3, 5 and 8, while h = 3 and the tree at position 1 falls right. It hits the tree at position 3 and it starts to fall too. In it's turn it hits the tree at position 5 and it also starts to fall. The distance between 8 and 5 is exactly 3, so the tree at position 8 will not fall.

As long as there are still trees standing, Wilbur will select either the leftmost standing tree with probability 0.5 or the rightmost standing tree with probability 0.5. Selected tree is then cut down. If there is only one tree remaining, Wilbur always selects it. As the ground is covered with grass, Wilbur wants to know the expected total length of the ground covered with fallen trees after he cuts them all down because he is concerned about his grass-eating cow friends. Please help Wilbur.

Input

The first line of the input contains two integers, n (1 ≤ n ≤ 2000) and h (1 ≤ h ≤ 108) and a real number p (0 ≤ p ≤ 1), given with no more than six decimal places.

The second line of the input contains n integers, x1, x2, ..., xn ( - 108 ≤ xi ≤ 108) in no particular order.

Output

Print a single real number — the expected total length of the ground covered by trees when they have all fallen down. Your answer will be considered correct if its absolute or relative error does not exceed 10 - 6.

Namely: let's assume that your answer is a, and the answer of the jury is b. The checker program will consider your answer correct, if .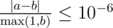

Sample Input

2 2 0.500000
1 2

Sample Output

3.250000000

HINT

 

题意

 在一个平面上有n棵树，每棵树高为h，你是一个伐木工人，每次有1/2的概率选择砍掉最左边或者最右边的树

树也有p的概率向左倒，(1-p)的概率向右倒 

树如果倒下的时候，压中了别的树，那么那棵树也会跟着倒下

然后问你，最后倒下的树的期望长度总和是多少

题解：

区间dp，dfs(l,r,f1,f2)

f1表示这个l-1这棵树是否倒向了右边，f2表示r+1这棵树是否倒向了左边

说是dp，实质上就是dfs，直接枚举所有的情况暴力dfs就好了

代码

#include<iostream>
#include<stdio.h>
#include<algorithm>
using namespace std;
#define maxn 2005
const int inf = 1e9;
double dp[maxn][maxn][2][2];
int vis[maxn][maxn][2][2];
int n;
double h,p;
int v[maxn];
int dl[maxn],dr[maxn];
double dfs(int l,int r,int f1,int f2)
{
    //cout<<l<<" "<<r<<" "<<f1<<" "<<f2<<endl;
    if(vis[l][r][f1][f2])return dp[l][r][f1][f2];
    if(l>r)return 0;
    vis[l][r][f1][f2]=1;
    double ans = dp[l][r][f1][f2];
    ans+=p*0.5*(min(h*1.00,v[l]-v[l-1]-f1*h)+dfs(l+1,r,0,f2));//最左边那个朝左边倒
    ans+=(1-p)*0.5*(min(h*1.0,v[r+1]-v[r]-f2*h)+dfs(l,r-1,f1,0));//最右边那个朝右边倒
    int L = dr[l];//左边向右边倒
    int R = dl[r];//右边向左边倒
    if(R<=l)ans+=p*0.5*(v[r]-v[l]+min(h,v[l]-v[l-1]-f1*h));
    else ans+=p*0.5*(v[r]-v[R]+h+dfs(l,R-1,f1,1));
    if(L>=r)ans+=(1-p)*0.5*(v[r]-v[l]+min(h,v[r+1]-v[r]-f2*h));
    else ans+=(1-p)*0.5*(v[L]-v[l]+h+dfs(L+1,r,1,f2));
    dp[l][r][f1][f2] = ans;
    return ans;
}
int main()
{
    scanf("%d%lf",&n,&h);
    scanf("%lf",&p);
    for(int i=1;i<=n;i++)
        scanf("%d",&v[i]);
    sort(v+1,v+1+n);
    v[n+1]=inf;
    v[0]=-inf;
    dr[n]=n;dl[1]=1;
    for(int i=n-1;i>=1;i--)
    {
        if(v[i+1]-v[i]<h)dr[i]=dr[i+1];
        else dr[i]=i;
    }
    for(int i=2;i<=n;i++)
    {
        if(v[i]-v[i-1]<h)dl[i]=dl[i-1];
        else dl[i]=i;
    }
    //cout<<dfs(1,n,0,0)<<endl;
    printf("%.15f\n",dfs(1,n,0,0));
}