Codeforces Round #329 (Div. 2) D. Happy Tree Party 树链剖分

D. Happy Tree Party

Time Limit: 20 Sec

Memory Limit: 256 MB

题目连接

http://codeforces.com/contest/593/problem/D

Description

Bogdan has a birthday today and mom gave him a tree consisting of n vertecies. For every edge of the tree i, some number x_i was written on it. In case you forget, a tree is a connected non-directed graph without cycles. After the present was granted, m guests consecutively come to Bogdan's party. When the i-th guest comes, he performs exactly one of the two possible operations:

Chooses some number y_i, and two vertecies a_i and b_i. After that, he moves along the edges of the tree from vertex a_i to vertex b_i using the shortest path (of course, such a path is unique in the tree). Every time he moves along some edge j, he replaces his current number y_i by 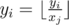$\text{[math]}$ , that is, by the result of integer division y_i div x_j.
Chooses some edge p_i and replaces the value written in it x_{p_i} by some positive integer c_i < x_{p_i}.

As Bogdan cares about his guests, he decided to ease the process. Write a program that performs all the operations requested by guests and outputs the resulting value y_i for each i of the first type.

Input

The first line of the input contains integers, n and m (2 ≤ n ≤ 200 000, 1 ≤ m ≤ 200 000) — the number of vertecies in the tree granted to Bogdan by his mom and the number of guests that came to the party respectively.

Next n - 1 lines contain the description of the edges. The i-th of these lines contains three integers u_i, v_i and x_i (1 ≤ u_i, v_i ≤ n, u_i ≠ v_i, 1 ≤ x_i ≤ 10¹⁸), denoting an edge that connects vertecies u_i and v_i, with the number x_i initially written on it.

The following m lines describe operations, requested by Bogdan's guests. Each description contains three or four integers and has one of the two possible forms:

1 a_i b_i y_i corresponds to a guest, who chooses the operation of the first type.
2 p_i c_i corresponds to a guests, who chooses the operation of the second type.

It is guaranteed that all the queries are correct, namely 1 ≤ a_i, b_i ≤ n, 1 ≤ p_i ≤ n - 1, 1 ≤ y_i ≤ 10¹⁸ and 1 ≤ c_i < x_{p_i}, where x_{p_i} represents a number written on edge p_i at this particular moment of time that is not necessarily equal to the initial value x_{p_i}, as some decreases may have already been applied to it. The edges are numbered from 1 to n - 1 in the order they appear in the input.

Output

For each guest who chooses the operation of the first type, print the result of processing the value y_i through the path from a_i to b_i.

Sample Input

Sample Output

HINT

题意

给你一颗树，然后有两个操作

1 x y z，假设x到y的链上边权分别为x1,x2,x3....，那么输出 [[[z/x1]/x2]/x3]

2 x y，把第x条边的边权改为y

题解：

有一个结论 [[[z/x1]/x2]/x3] = [z/(x1*x2*x3)]

那么我们只要维护区间乘积就好了，树链剖分裸题

但是区间乘积很容易爆LL，那么我们就用一个log来判断，如果爆了ll，那就直接把他置为1e18

然后答案直接输出0就好了

代码

#include <iostream>
#include <string.h>
#include <algorithm>
#include <stdio.h>
#include <math.h>
using namespace std;
const int N=800010;
const int INF=1<<30;

int n,tim;

long long num[N];
int siz[N],top[N],son[N];
int dep[N],tid[N],Rank[N],fa[N];
int head[N],to[2*N],Next[2*N],w[2*N],edge;
int flag = 0;
struct Edge
{
    int u,v;
    long long c;
};
Edge tmp[2*N];

void Init()
{
    memset(head,-1,sizeof(head));
    memset(son,-1,sizeof(son));
    tim=0;
    edge=0;
}

void addedge(int u,int v,int c)
{
    to[edge]=v,w[edge]=c,Next[edge]=head[u],head[u]=edge++;
    to[edge]=u,w[edge]=c,Next[edge]=head[v],head[v]=edge++;
}

//树链剖分部分
void dfs1(int u,int father,int d)
{
    dep[u]=d;
    fa[u]=father;
    siz[u]=1;
    for(int i=head[u]; ~i; i=Next[i])
    {
        int v=to[i];
        if(v!=father)
        {
            dfs1(v,u,d+1);
            siz[u]+=siz[v];
            if(son[u]==-1||siz[v]>siz[son[u]])
                son[u]=v;
        }
    }
}

void dfs2(int u,int tp)
{
    top[u]=tp;
    tid[u]=++tim;
    Rank[tid[u]]=u;
    if(son[u]==-1) return;
    dfs2(son[u],tp);
    for(int i=head[u]; ~i; i=Next[i])
    {
        int v=to[i];
        if(v!=son[u]&&v!=fa[u])
            dfs2(v,v);
    }
}

//线段树部分
#define lson l,mid,rt<<1
#define rson mid+1,r,rt<<1|1
const long long kkk = 1e18+28;
long long MAX[4*N];

void PushUP(int rt)
{
    if(MAX[rt<<1]==0)
        MAX[rt]=1;
    if(MAX[rt<<1|1]==0)
        MAX[rt<<1|1]=1;
    double ppp1 = MAX[rt<<1];
    double ppp2 = MAX[rt<<1|1];
    if(log(ppp1) + log(ppp2) > log(kkk * 1.0))
        MAX[rt]=kkk+5;
    else
        MAX[rt]=MAX[rt<<1]*MAX[rt<<1|1];
}

void Build(int l,int r,int rt)
{
    if(l==r)
    {
        MAX[rt]=num[l];
        return;
    }
    int mid=(l+r)>>1;
    Build(lson);
    Build(rson);
    PushUP(rt);
}

void Update(int l,int r,int rt,int p,long long val)
{
    if(l==r)
    {
        MAX[rt]=val;
        return;
    }
    int mid=(l+r)>>1;
    if(p<=mid)
        Update(lson,p,val);
    else
        Update(rson,p,val);
    PushUP(rt);
}

long long Query(int l,int r,int rt,int L,int R)
{
    if(L<=l&&R>=r)
        return MAX[rt];
    int mid=(l+r)>>1;
    long long ans=1;
    if(L<=mid)
    {
        long long kkkk = Query(lson,L,R);
        if(kkkk==-1)
            flag = 1;
        if(log(ans*1.0) + log(kkkk*1.0) > log(kkk*1.0))
            ans = kkk+203;
        else
            ans*=kkkk;
    }
    if(R>mid)
    {
        long long kkkk = Query(rson,L,R);
        if(kkkk==-1)
            flag = 1;
        if(log(ans*1.0) + log(kkkk*1.0) > log(kkk*1.0))
            ans = kkk+203;
        else
            ans*=kkkk;
    }
    return ans;
}

void Change(int x,long long val)
{
    if(dep[tmp[x].u]>dep[tmp[x].v])
        Update(2,n,1,tid[tmp[x].u],val);
    else
        Update(2,n,1,tid[tmp[x].v],val);
}

long long query(int x,int y)
{
    long long ans=1;
    while(top[x]!=top[y])
    {
        if(dep[top[x]]<dep[top[y]]) swap(x,y);
        long long kkkk = Query(2,n,1,tid[top[x]],tid[x]);
        if(log(ans*1.0) + log(kkkk*1.0) > log(kkk*1.0))
            ans = kkk+203;
        else
            ans*=kkkk;
        x=fa[top[x]];
    }
    if(dep[x]>dep[y]) swap(x,y);
    if(x!=y)
    {
        long long kkkk =Query(2,n,1,tid[x]+1,tid[y]);
        if(log(ans*1.0) + log(kkkk*1.0) > log(kkk*1.0))
            ans = kkk+203;
        else
            ans*=kkkk;
    }
    return ans;
}
int MM;
int main()
{
    char oper[15];
    int a,b;
    long long c;
    Init();
    scanf("%d%d",&n,&MM);
    for(int i=1; i<n; i++)
    {
        scanf("%d%d%lld",&a,&b,&c);
        tmp[i].u=a;tmp[i].v=b;tmp[i].c=c;
        addedge(a,b,c);
    }
    dfs1(1,1,1);
    dfs2(1,1);
    //用边的孩子节点来表示该边
    for(int i=1;i<n;i++)
    {
        if(dep[tmp[i].u]>dep[tmp[i].v])
            num[tid[tmp[i].u]]=tmp[i].c;
        else
            num[tid[tmp[i].v]]=tmp[i].c;
    }
    Build(2,n,1);
    while(MM--)
    {
        scanf("%s",oper);
        if(oper[0]=='1')
        {
            long long ppp;
            scanf("%d%d",&a,&b);
            scanf("%lld",&ppp);
            flag = 0;
            long long dddd = query(a,b);
            printf("%lld\n",ppp/dddd);
        }
        else
        {
            long long ppp;
            scanf("%d%lld",&a,&ppp);
            Change(a,ppp);
        }
    }
    return 0;
}

posted @ 2015-11-05 09:47 qscqesze 阅读(637) 评论(0) 编辑收藏举报

刷新页面返回顶部

qscqesze

躺尸选手

Codeforces Round #329 (Div. 2) D. Happy Tree Party 树链剖分

D. Happy Tree Party

题目连接

Description

HINT