Codeforces Round #250 (Div. 1) D. The Child and Sequence 线段树 区间取摸

D. The Child and Sequence

Time Limit: 20 Sec

Memory Limit: 256 MB

题目连接

http://codeforces.com/contest/438/problem/D

Description

At the children's day, the child came to Picks's house, and messed his house up. Picks was angry at him. A lot of important things were lost, in particular the favorite sequence of Picks.

Fortunately, Picks remembers how to repair the sequence. Initially he should create an integer array a[1], a[2], ..., a[n]. Then he should perform a sequence of m operations. An operation can be one of the following:

1. Print operation l, r. Picks should write down the value of .
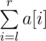2. Modulo operation l, r, x. Picks should perform assignment a[i] = a[i] mod x for each i (l ≤ i ≤ r).
3. Set operation k, x. Picks should set the value of a[k] to x (in other words perform an assignment a[k] = x).

Can you help Picks to perform the whole sequence of operations?

Input

The first line of input contains two integer: n, m (1 ≤ n, m ≤ 10⁵). The second line contains n integers, separated by space: a[1], a[2], ..., a[n] (1 ≤ a[i] ≤ 10⁹) — initial value of array elements.

Each of the next m lines begins with a number type .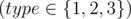

• If type = 1, there will be two integers more in the line: l, r (1 ≤ l ≤ r ≤ n), which correspond the operation 1.
• If type = 2, there will be three integers more in the line: l, r, x (1 ≤ l ≤ r ≤ n; 1 ≤ x ≤ 10⁹), which correspond the operation 2.
• If type = 3, there will be two integers more in the line: k, x (1 ≤ k ≤ n; 1 ≤ x ≤ 10⁹), which correspond the operation 3.

 

Output

For each operation 1, please print a line containing the answer. Notice that the answer may exceed the 32-bit integer.

 

Sample Input

5 5
1 2 3 4 5
2 3 5 4
3 3 5
1 2 5
2 1 3 3
1 1 3

Sample Output

8
5

HINT

 

题意

给你n个数，三个操作

1.输出[l,r]的和

2.将[l,r]中的数，对v取摸

3.把a[x]变成v

题解：

线段树

区间定值和区间和很简单

区间取摸的话，需要维护一个区间最大值，如果这个区间的最大值小于要取摸的数，那么就直接break就好了

代码

 

#include<iostream>
#include<stdio.h>
using namespace std;
#define maxn 100005
struct node
{
    int l,r;
    long long mx,sum;
}a[maxn*4];
int d[maxn];
void build(int x,int l,int r)
{
    a[x].l = l,a[x].r = r;
    if(l==r)
    {
        a[x].mx = a[x].sum = d[l];
        return;
    }
    int mid = (l+r)/2;
    build(x<<1,l,mid);
    build(x<<1|1,mid+1,r);
    a[x].mx = max(a[x<<1].mx , a[x<<1|1].mx);
    a[x].sum = a[x<<1|1].sum + a[x<<1].sum;
}
void change(int x,int pos,long long val)
{
    int l = a[x].l,r = a[x].r;
    if(l==r)
    {
        a[x].mx = a[x].sum = val;
        return;
    }
    int mid = (l+r)/2;
    if(pos<=mid)
        change(x<<1,pos,val);
    else
        change(x<<1|1,pos,val);
    a[x].mx = max(a[x<<1].mx,a[x<<1|1].mx);
    a[x].sum = a[x<<1].sum + a[x<<1|1].sum;
}
void mod(int x,int l,int r,long long val)
{
    int L = a[x].l,R = a[x].r;
    if(a[x].mx<val)return;
    if(L==R)
    {
        a[x].sum%=val;
        a[x].mx%=val;
        return;
    }
    int mid = (L+R)/2;
    if(r<=mid)
        mod(x<<1,l,r,val);
    else if(l>mid)
        mod(x<<1|1,l,r,val);
    else mod(x<<1,l,mid,val),mod(x<<1|1,mid+1,r,val);
    a[x].sum = a[x<<1].sum + a[x<<1|1].sum;
    a[x].mx = max(a[x<<1].mx,a[x<<1|1].mx);
}
long long get(int x,int l,int r)
{
    int L = a[x].l,R = a[x].r;
    if(L>=l&&R<=r)
    {
        return a[x].sum;
    }
    int mid = (L+R)/2;
    long long sum1 = 0,sum2 = 0;
    if(r<=mid)
        sum1 = get(x<<1,l,r);
    else if(l>mid)
        sum2 = get(x<<1|1,l,r);
    else sum1 = get(x<<1,l,mid),sum2 = get(x<<1|1,mid+1,r);
    return sum1 + sum2;
}
int main()
{
    int n,q;
    scanf("%d%d",&n,&q);
    for(int i=1;i<=n;i++)
        scanf("%d",&d[i]);
    build(1,1,n);
    while(q--)
    {
        int op;
        scanf("%d",&op);
        if(op==1)
        {
            int x,y;scanf("%d%d",&x,&y);
            printf("%lld\n",get(1,x,y));
        }
        if(op==2)
        {
            int x,y,z;scanf("%d%d%d",&x,&y,&z);
            mod(1,x,y,z);
        }
        if(op==3)
        {
            int x,y;scanf("%d%d",&x,&y);
            change(1,x,y);
        }
    }
}