HDU 5476 Explore Track of Point 数学平几

Explore Track of Point

Time Limit: 1 Sec  

Memory Limit: 256 MB

题目连接

http://acm.hdu.edu.cn/showproblem.php?pid=5476

Description

In Geometry, the problem of track is very interesting. Because in some cases, the track of point may be beautiful curve. For example, in polar Coordinate system, ρ=cos3θ is like rose, ρ=1−sinθ is a Cardioid, and so on. Today, there is a simple problem about it which you need to solve.

Give you a triangle ΔABC and AB = AC. M is the midpoint of BC. Point P is in ΔABC and makes min{∠MPB+∠APC,∠MPC+∠APB} maximum. The track of P is Γ. Would you mind calculating the length of Γ?

Given the coordinate of A, B, C, please output the length of Γ.

Input

There are T (1≤T≤104) test cases. For each case, one line includes six integers the coordinate of A, B, C in order. It is guaranteed that AB = AC and three points are not collinear. All coordinates do not exceed 104 by absolute value.

Output

For each case, first please output "Case #k: ", k is the number of test case. See sample output for more detail. Then, please output the length of Γ with exactly 4 digits after the decimal point.

Sample Input

1
0 1 -1 0 1 0

 

Sample Output

Case #1: 3.2214

HINT

 

题意

给你一个等腰三角形，底边中点叫做M，找一个点P的轨迹

使得  {∠MPB+∠APC,∠MPC+∠APB} 的最小值最大，问这个轨迹的长度是多少，这个轨迹必须在三角形内

题解：

 

下面这个圆弧再加上垂线的长度就好了

证明是转载的

 

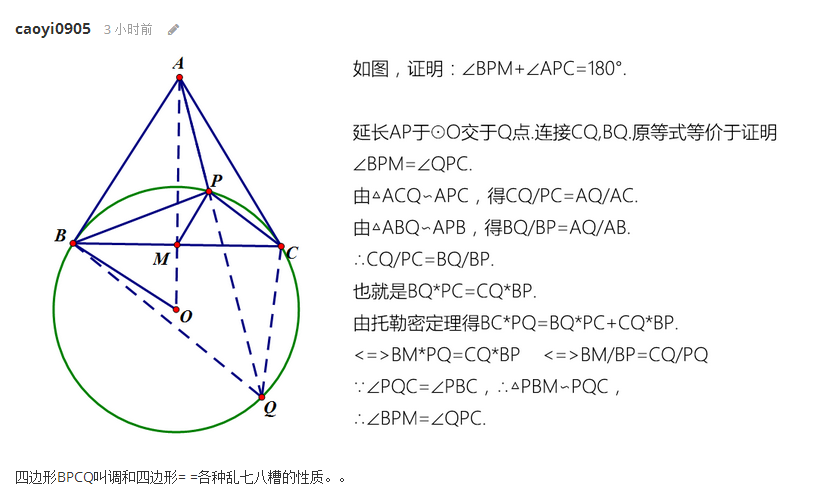
代码：

//qscqesze
#pragma comment(linker, "/STACK:1024000000,1024000000")
#include <cstdio>
#include <cmath>
#include <cstring>
#include <ctime>
#include <iostream>
#include <algorithm>
#include <set>
#include <bitset>
#include <vector>
#include <sstream>
#include <queue>
#include <typeinfo>
#include <fstream>
#include <map>
#include <stack>
typedef long long ll;
using namespace std;
//freopen("D.in","r",stdin);
//freopen("D.out","w",stdout);
#define sspeed ios_base::sync_with_stdio(0);cin.tie(0)
#define maxn 100006
#define mod 1000000007
#define eps 1e-9
#define e exp(1.0)
#define PI acos(-1)
const double EP  = 1E-10 ;
int Num;
//const int inf=0x7fffffff;
const ll inf=999999999;
inline ll read()
{
    ll x=0,f=1;char ch=getchar();
    while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();}
    while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();}
    return x*f;
}
//*************************************************************************************

int main()
{
    int t=read();
    for(int cas=1;cas<=t;cas++)
    {
        double x1,y1,x2,y2,x3,y3;
        scanf("%lf%lf%lf%lf%lf%lf",&x1,&y1,&x2,&y2,&x3,&y3);
        double a = sqrt((x1-x2)*(x1-x2)+(y1-y2)*(y1-y2));
        double b = sqrt((x1-x3)*(x1-x3)+(y1-y3)*(y1-y3));
        double c = sqrt((x2-x3)*(x2-x3)+(y2-y3)*(y2-y3));

        double k = acos((a*a+b*b-c*c)/(2.0*a*b));

        double ans = cos(0.5*k)*a;
        //cout<<k<<endl;
        double h = cos(0.5*k)*a;
        double r = (a*c)/(h*2.0);
        ans += r*((double)PI-k);
        /*
        if(k<=PI/2.0)
            ans += k*a;
        else
        {
            double aa = a;
            double bb = cos(0.5*k)*a;
            double cc = c/2.0;

            double h = 2.0*bb*cc/aa;
            double kk = acos(h/aa);
            double kkk = k - 4.0*kk;
            kkk = max(0.0,kkk);
            ans += kkk*a;
        }
        */
        printf("Case #%d: %.4lf\n",cas,ans);
    }
}