Codeforces Round #298 (Div. 2) E. Berland Local Positioning System 构造

E. Berland Local Positioning System

Time Limit: 1 Sec  Memory Limit: 256 MB

题目连接

http://codeforces.com/contest/534/problem/E

Description

In Berland a bus travels along the main street of the capital. The street begins from the main square and looks like a very long segment. There are n bus stops located along the street, the i-th of them is located at the distance a_i from the central square, all distances are distinct, the stops are numbered in the order of increasing distance from the square, that is, a_i < a_i + 1 for all i from 1 to n - 1. The bus starts its journey from the first stop, it passes stops 2, 3 and so on. It reaches the stop number n, turns around and goes in the opposite direction to stop 1, passing all the intermediate stops in the reverse order. After that, it again starts to move towards stop n. During the day, the bus runs non-stop on this route.

The bus is equipped with the Berland local positioning system. When the bus passes a stop, the system notes down its number.

One of the key features of the system is that it can respond to the queries about the distance covered by the bus for the parts of its path between some pair of stops. A special module of the system takes the input with the information about a set of stops on a segment of the path, a stop number occurs in the set as many times as the bus drove past it. This module returns the length of the traveled segment of the path (or -1 if it is impossible to determine the length uniquely). The operation of the module is complicated by the fact that stop numbers occur in the request not in the order they were visited but in the non-decreasing order.

For example, if the number of stops is 6, and the part of the bus path starts at the bus stop number 5, ends at the stop number 3 and passes the stops as follows: 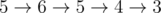, then the request about this segment of the path will have form: 3, 4, 5, 5, 6. If the bus on the segment of the path from stop 5 to stop 3 has time to drive past the 1-th stop (i.e., if we consider a segment that ends with the second visit to stop 3 on the way from 5), then the request will have form: 1, 2, 2, 3, 3, 4, 5, 5, 6.

You will have to repeat the Berland programmers achievement and implement this function.

Input

The first line contains integer n (2 ≤ n ≤ 2·10⁵) — the number of stops.

The second line contains n integers (1 ≤ a_i ≤ 10⁹) — the distance from the i-th stop to the central square. The numbers in the second line go in the increasing order.

The third line contains integer m (1 ≤ m ≤ 4·10⁵) — the number of stops the bus visited on some segment of the path.

The fourth line contains m integers (1 ≤ b_i ≤ n) — the sorted list of numbers of the stops visited by the bus on the segment of the path. The number of a stop occurs as many times as it was visited by a bus.

It is guaranteed that the query corresponds to some segment of the path.

Output

In the single line please print the distance covered by a bus. If it is impossible to determine it unambiguously, print  - 1.

Sample Input

Input

6
2 3 5 7 11 13
5
3 4 5 5 6

 

Input

6
2 3 5 7 11 13
9
1 2 2 3 3 4 5 5 6

 

Input

3
10 200 300
4
1 2 2 3

 

Input

3
1 2 3
4
1 2 2 3

Sample Output

Output

10

Output

16

Output

-1

Output

3

HINT

The first test from the statement demonstrates the first example shown in the statement of the problem.

The second test from the statement demonstrates the second example shown in the statement of the problem.

In the third sample there are two possible paths that have distinct lengths, consequently, the sought length of the segment isn't defined uniquely.

In the fourth sample, even though two distinct paths correspond to the query, they have the same lengths, so the sought length of the segment is defined uniquely.

题意

给你过车站的顺序，然后让你输出车走的距离，如果这个距离不是唯一的，直接输出-1

题解：

输出-1的情况只有一种，就是路过所有点的次数都相等（除了首部和尾部），且，每条边的长度有一种不相等

其他情况直接暴力搞搞就好了

代码转自黄学长：@hzwer

代码：

 

//qscqesze
#include <cstdio>
#include <cmath>
#include <cstring>
#include <ctime>
#include <iostream>
#include <algorithm>
#include <set>
#include <vector>
#include <sstream>
#include <queue>
#include <typeinfo>
#include <fstream>
#include <map>
typedef long long ll;
using namespace std;
//freopen("D.in","r",stdin);
//freopen("D.out","w",stdout);
#define sspeed ios_base::sync_with_stdio(0);cin.tie(0)
#define maxn 200001
#define mod 10007
#define eps 1e-9
//const int inf=0x7fffffff;   //无限大
const int inf=0x3f3f3f3f;
/*
inline ll read()
{
    int x=0,f=1;char ch=getchar();
    while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();}
    while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();}
    return x*f;
}
int buf[10];
inline void write(int i) {
  int p = 0;if(i == 0) p++;
  else while(i) {buf[p++] = i % 10;i /= 10;}
  for(int j = p-1; j >=0; j--) putchar('0' + buf[j]);
  printf("\n");
}
*/
//**************************************************************************************

ll a[maxn];
ll b[maxn];
int main()
{
    ll mx=0,mi=inf;
    int n;
    cin>>n;
    for(int i=1;i<=n;i++)
        scanf("%d",&a[i]);
    int m;
    cin>>m;
    for(int i=1;i<=m;i++)
    {
        int x;
        scanf("%d",&x);
        b[x]++;
        if(x==1||x==n)
            b[x]++;
    }
    for(int i=1;i<=n;i++)
    {
        mx=max(mx,b[i]);
        mi=min(mi,b[i]);
    }
    //cout<<mi<<" "<<mx<<endl;
    if(mi==mx)
    {
        int flag=0;
        for(int i=1;i<=n-2;i++)
        {
            if(a[i+1]-a[i]!=a[i+2]-a[i+1])
            {
                flag=1;
                break;
            }
        }
        if(flag)
            puts("-1");
        else
            printf("%lld",(a[n]-a[1])*mi-(a[2]-a[1]));
    }
    else
    {
        ll ans=0;
        for(int i=2;i<=n;i++)
        {
            ans+=(a[i]-a[i-1])*min(b[i],b[i-1]);
            //cout<<ans<<endl;
        }
        cout<<ans<<endl;
    }

}