HDU 4162 Shape Number 最小表示法

Shape Number

Time Limit: 24000/12000 MS (Java/Others)    Memory Limit: 32768/32768 K (Java/Others)
Total Submission(s): 981    Accepted Submission(s): 471

Problem Description

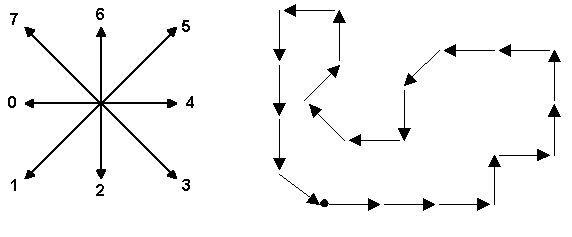
In computer vision, a chain code is a sequence of numbers representing directions when following the contour of an object. For example, the following figure shows the contour represented by the chain code 22234446466001207560 (starting at the upper-left corner).

Two chain codes may represent the same shape if the shape has been rotated, or if a different starting point is chosen for the contour. To normalize the code for rotation, we can compute the first difference of the chain code instead. The first difference is obtained by counting the number of direction changes in counterclockwise direction between consecutive elements in the chain code (the last element is consecutive with the first one). In the above code, the first difference is

00110026202011676122
Finally, to normalize for the starting point, we consider all cyclic rotations of the first difference and choose among them the lexicographically smallest such code. The resulting code is called the shape number.
00110026202011676122
01100262020116761220
11002620201167612200
...
20011002620201167612
In this case, 00110026202011676122 is the shape number of the shape above.

 

 

Input

The input consists of a number of cases. The input of each case is given in one line, consisting of a chain code of a shape. The length of the chain code is at most 300,000, and all digits in the code are between 0 and 7 inclusive. The contour may intersect itself and needs not trace back to the starting point.

 

 

Output

For each case, print the resulting shape number after the normalizations discussed above are performed.

 

 

Sample Input

22234446466001207560 12075602223444646600

 

 

Sample Output

00110026202011676122 00110026202011676122

 

#include <cstdio>
#include <cmath>
#include <cstring>
#include <ctime>
#include <iostream>
#include <algorithm>
#include <set>
#include <vector>
#include <sstream>
#include <queue>
#include <typeinfo>
#include <fstream>
typedef long long ll;
using namespace std;
//freopen("D.in","r",stdin);
//freopen("D.out","w",stdout);
#define sspeed ios_base::sync_with_stdio(0);cin.tie(0)
#define maxn 300005
const int inf=0x7fffffff;   //无限大
string s;
char b[maxn];

int getminsub(char *a)
{
    int i=0,j=1,len=strlen(a),k=0; //取两个同构的字符串一个从下标0开始，一个从下标1开始
    while(i<len&&j<len&&k<len) //这里并没有将字符串复制一份添加到后面
    {
        if(k==len) break; //说明找到了a的最小表示
        if(i==j) j++;
        int ni=i+k,nj = j+k;
        if(ni>=len) ni-=len; //就是回到字符串的开始去
        if(nj>=len) nj-=len;
        if(a[ni]>a[nj])
        {
            i+=k+1;
            k=0;
        }
        else if(a[ni]<a[nj])
        {
            j+=k+1;
            k=0;
        }
        else k++;
    }
    return  i; //返回从第i个字符开始时a的最小表示
}

int main()
{
    while(cin>>s)
    {
        int n=s.size();
        for(int i=0;i<s.size();i++)
        {
            if(s[(i+1)%n]>=s[i])
                b[i]=(s[(i+1)%n]-s[i])+'0';
            else
                b[i]=s[(i+1)%n]+8-s[i]+'0';
        }

        int k=getminsub(b);
        for(int i=k;i<s.size()+k;i++)
        {
            cout<<b[i%n];
        }
        cout<<endl;
    }
}